
5-4一维简谐运动的合成拍现象 物理学教程 (第二版) 两个同方向同频率简谐运动的合成 〔七=Acos(wt+p,) Lx,A2 cos(ct+p2) x=x+X2 x=Acos(@t+o) A X2 A=V4+号+2A4,c0s(p,-0) A sin p+2 sin p2 两个同方向同频 tan⑩= 率简谐运动合成 A cos+42 cosz 后仍为简谐运动 第五章机械振动
物理学教程 (第二版) 第五章 机械振动 5 – 4 一维简谐运动的合成 拍现象 1 A1 1 x x 0 一 两个同方向同频率简谐运动的合成 1 2 x = x + x 1 1 2 2 1 1 2 2 cos cos sin sin tan A A A A + + = 2 cos( ) 1 2 2 1 2 2 2 A = A1 + A + A A − x = Acos(t +) cos( ) 1 = 1 +1 x A t cos( ) 2 = 2 +2 x A t A x2 x A2 2 两个同方向同频 率简谐运动合成 后仍为简谐运动
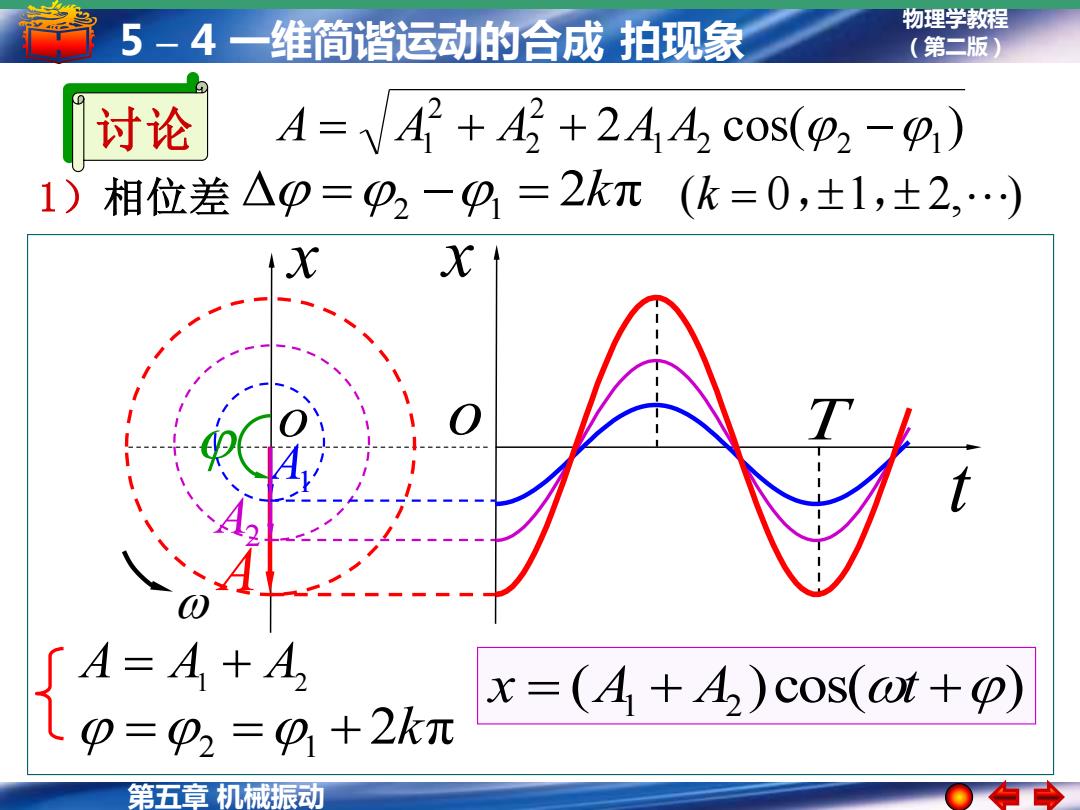
5-4一维简谐运动的合成拍现象 物理学教程 (第二版) 讨论 A=A2+2+244 cos(o2-) 1) 相位差△p=p2-9=2kπ(k=0,±1,±2,…) X X 「A=A+A x=(A+4)cos(at+o) P=p2=9+2kπ 第五章机械振动
物理学教程 (第二版) 第五章 机械振动 5 – 4 一维简谐运动的合成 拍现象 x x t o o =2 =1 + 2kπ ( )cos( ) x = A1 + A2 t + A A = A1 + A2 A1 A2 T 1)相位差 =2 −1 = 2kπ (k = 0,1, 2, ) 2 cos( ) 1 2 2 1 2 2 2 讨论 A = A1 + A + A A −
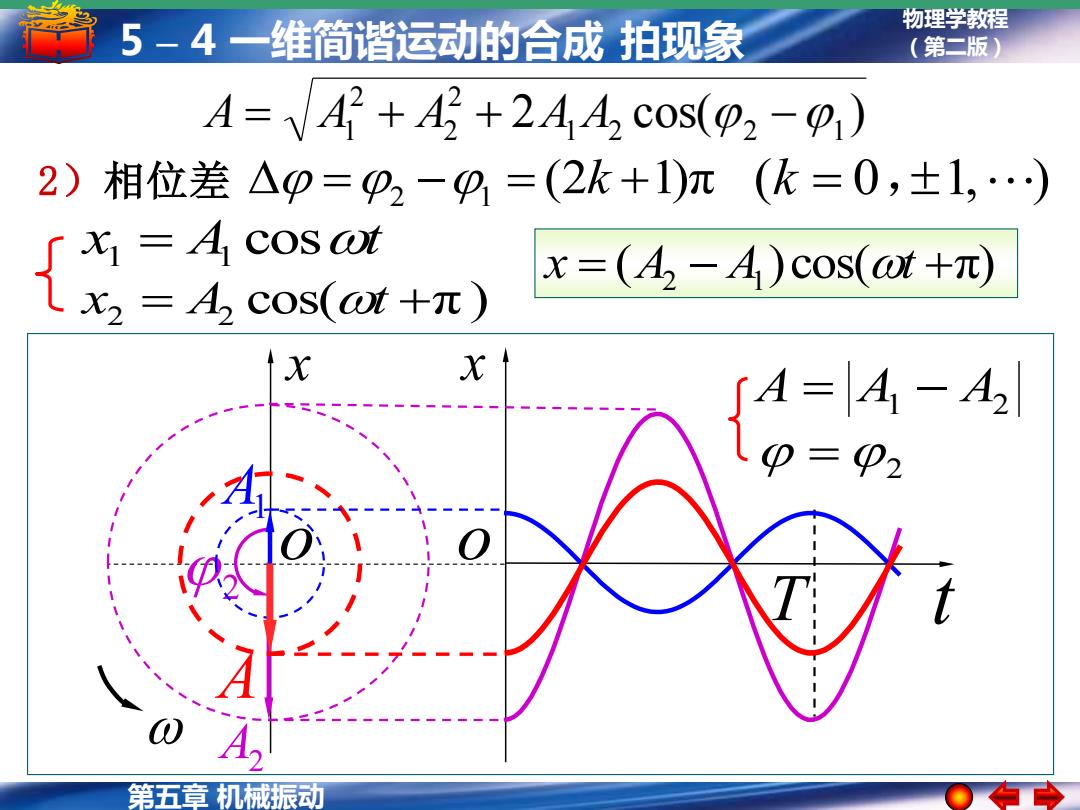
5-4一维简谐运动的合成拍现象 物理学教程 (第二版) A=42+42+244 cos(2-) 2)相位差△p=p2-9=(2k+1)m(k=0,±1,) x=4 cosot X2=A,cos(ot+π) x=(A,2-A)cos(@t+π) x X ∫A=A1-A2 0=2 A 第五章机械振动 点
物理学教程 (第二版) 第五章 机械振动 5 – 4 一维简谐运动的合成 拍现象 x x t o o A = A1 − A2 = 2 ( )cos( π) x = A2 − A1 t + 2 cos( ) 1 2 2 1 2 2 2 A = A1 + A + A A − T A2 2 A1 A 2)相位差 =2 −1 = (2k +1)π (k = 0,1, ) x A cost 1 = 1 cos( π ) x2 = A2 t +

5-4一维简谐运动的合成拍现象 物理学教程 (第二版) A=A2+2+244 cos(2-) 相位差 △p=p2-P1 1)相位差 △0=2k元 (k=0,±1,…) A=4+4 相互加强 2)相位差 △p=(2k+1)π (k=0,±1,…) A=4-4 相互削弱 3)一般情况 A+A>A>A-4 第五章机械振动
物理学教程 (第二版) 第五章 机械振动 5 – 4 一维简谐运动的合成 拍现象 3)一般情况 A1 + A2 A A1 − A2 A = A1 − A2 2)相位差 1)相位差 A = A1 + A2 = 2k π (k = 0,1,) 相互加强 相互削弱 = (2k +1) π (k = 0,1,) ➢ 相位差 =2 −1 2 cos( ) 1 2 2 1 2 2 2 A = A1 + A + A A −

5-4一维简谐运动的合成拍现象 物理学教程 (第二版) *二多个同方向同频率简谐运动的合成 x-A cos(@t+) x2=42 cos(ot+p2) x=A cos(at+e) X=X1+X2++m X x=AcOS(⊙t+p) 多个同方向同频率简谐运动合成仍为简谐运动 第五章机械振动
物理学教程 (第二版) 第五章 机械振动 5 – 4 一维简谐运动的合成 拍现象 1 A1 x o * 二 多个同方向同频率简谐运动的合成 A2 2 A3 3 x = Acos(t +) n x = x + x ++ x 1 2 cos( ) 1 = 1 +1 x A t cos( ) 2 = 2 +2 x A t cos( ) n n n x = A t + A 多个同方向同频率简谐运动合成仍为简谐运动