南京大学：《电动力学 Electrodynamics》课程教学资源（课件讲稿）第一章 电磁现象的普遍规律 Universal Law of Electromagnetic Phenomenon

4、高斯定理(Gauss?theorem) 现在，具体分析一下电荷分布产生的电场E() 的一般性质。所谓电场其实是带电体周围的一个特 殊空间，特殊性表现在：当我们在这个空间放入一 个点电荷时，该电荷会受到作用力。 Gauss'theorem主要是讨论电场强度E()的面积 分，在点电荷场中，设s表示包围着点电荷g的一个 闭合面，d5为s上的定向面元，以外法线方向为正。 21

4、高斯定理（Gauss’ theorem) 现在，具体分析一下电荷分布产生的电场 的一般性质。所谓电场其实是带电体周围的一个特 殊空间，特殊性表现在：当我们在这个空间放入一 个点电荷时，该电荷会受到作用力。 Gauss’ theorem主要是讨论电场强度 的面积 分，在点电荷场中，设s表示包围着点电荷q的一个 闭合面， 为s上的定向面元，以外法线方向为正。 E(x)   21 E(x)   ds 

a)如果点电荷g在s面内 ds S ds do 对于空间任一封闭曲面S作E的面积分，可得 推导 行w=月n 60 22

a) 如果点电荷q在s面内 θ S q r E  ds  d ds  22 对于空间任一封闭曲面S作 的面积分，可得 推导 E  0 0 4  q d q E ds S S        

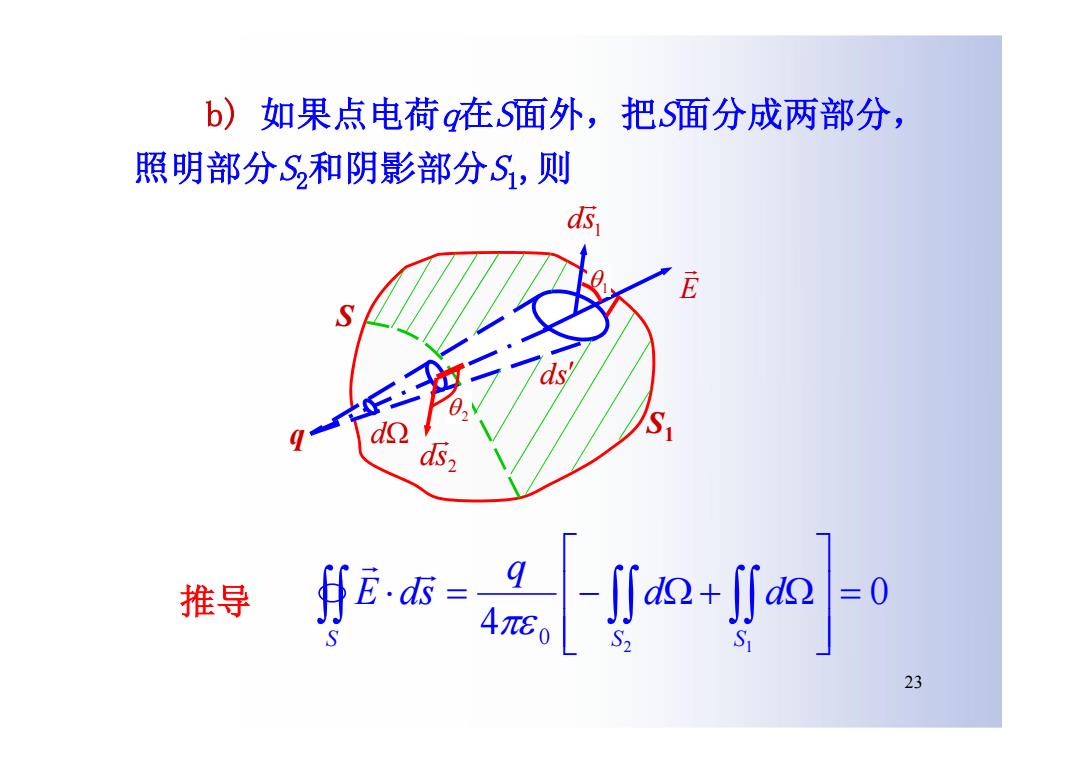
b)如果点电荷q在S面外，把S面分成两部分， 照明部分S2和阴影部分S,则 d E S 推导 标-品n网 0 23

b) 如果点电荷q在S面外，把S面分成两部分， 照明部分S2和阴影部分S1 ,则 S q E  1 ds  d ds S1  2 1 2 ds  23 0 4 2 1 0               S S S d d q E ds    推导

由此可得到结论： q在S面内 0 9在S面外 根据叠加原理，在点电荷系场中，则存在着如下形 式： 开E压=川（瓦+E2+…+瓦++E)西 设q1,2,…q在S内，qk1,9+2,…qn在S外，则有 i云-立 S面内 对于连续分布的电荷体系来说，则有 f月E=Mr Eo v 24

由此可得到结论： 根据叠加原理，在点电荷系场中，则存在着如下形 式： 设q1 ,q2 ,···qk在S内，qk+1,qk+2,···qn在S外，则有 对于连续分布的电荷体系来说，则有 0 0         在 面外 在 面内 q S q S q E dS S              S k n S E dS E E E E ds          ( ) 1 2 0 1 0 1   q E dS q k i i S        24 S面内     S V E ds d  0   1

5、静电场的散度(divergence of electrostatic field) 方法一： 已知 付E杏名Jawr展omt 月a6=∫ir 得到 月Es=∫V:idr 将此与Gauss定理比较，得到 25

5、静电场的散度（divergence of electrostatic field) 方法一： 已知 根据Gauss公式： 将此与Gauss定理比较，得到     S V E ds d  0   1      S V A ds Ad         S V E ds Ed        V V Ed d   0  1 得到 25