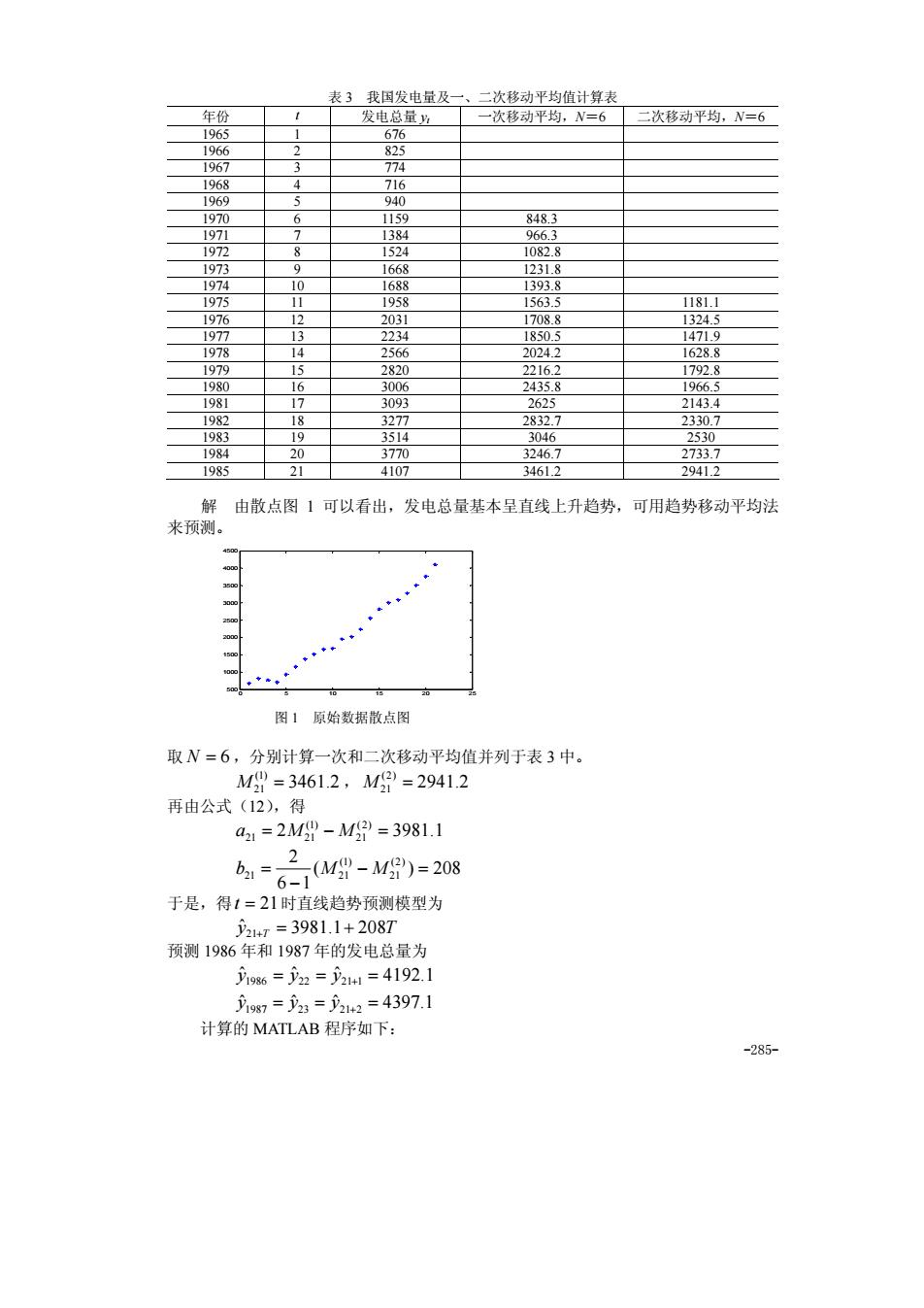
表}我国发电量及 平1 二次移动平均,N=6 231.8 1181. 216 0 214 230 4612 27 解由散点图1可以看出,发电总量基本呈直线上升趋势,可用趋势移动平均法 来预测 图1原始数据散点图 取N=6,分别计算一次和二次移动平均值并列于表3中。 M"=3461.2,M=2941.2 再由公式(12),得 a21=2M-M2=3981.1 6=6M-M)=208 2 于是,得1=21时直线趋势预测模型为 y4=y2=y2=4192. =2:=2=4397.1 计算的MATLAB程序如下: -285
-285- 表 3 我国发电量及一、二次移动平均值计算表 年份 t 发电总量 yt 一次移动平均,N=6 二次移动平均,N=6 1965 1 676 1966 2 825 1967 3 774 1968 4 716 1969 5 940 1970 6 1159 848.3 1971 7 1384 966.3 1972 8 1524 1082.8 1973 9 1668 1231.8 1974 10 1688 1393.8 1975 11 1958 1563.5 1181.1 1976 12 2031 1708.8 1324.5 1977 13 2234 1850.5 1471.9 1978 14 2566 2024.2 1628.8 1979 15 2820 2216.2 1792.8 1980 16 3006 2435.8 1966.5 1981 17 3093 2625 2143.4 1982 18 3277 2832.7 2330.7 1983 19 3514 3046 2530 1984 20 3770 3246.7 2733.7 1985 21 4107 3461.2 2941.2 解 由散点图 1 可以看出,发电总量基本呈直线上升趋势,可用趋势移动平均法 来预测。 0 5 10 15 20 25 500 1000 1500 2000 2500 3000 3500 4000 4500 图 1 原始数据散点图 取 N = 6 ,分别计算一次和二次移动平均值并列于表 3 中。 3461.2 (1) M21 = , 2941.2 (2) M21 = 再由公式(12),得 2 3981.1 (2) 21 (1) a21 = M21 − M = ( ) 208 6 1 2 (2) 21 (1) 21 21 − = − b = M M 于是,得t = 21时直线趋势预测模型为 yˆ21+T = 3981.1+ 208T 预测 1986 年和 1987 年的发电总量为 yˆ1986 = yˆ22 = yˆ21+1 = 4192.1 yˆ1987 = yˆ23 = yˆ21+2 = 4397.1 计算的 MATLAB 程序如下:

clc.clear %把原始数据保存在纯文本文件y.t中 h %n为移动平均的项数 for i=1:ml-n+l yhatl(i)=sum(y(i:i+n-1))/n, end yhatl f-engh6yha1方 yhat2(i)=sum(yhat1(i:i+n-1)//n; end plot(1:21.y*) a21yhatl(end)-yhat2(end) 19nd-yhat2(end)/(n-1) y1987=a21+2*b21 趋势移动平均法对于同时存在直线趋势与周期波动的序列,是一种既能反映趋势变 化,又可以有效地分离出来周期变动的方法 §3指数平滑法 一次移动平均实际上认为最近N期数据对未来值影响相同,都加权:而N期 以前的数据对未来值没有影响,加权为0。但是,二次及更高次移动平均数的权数却不 是,且次数越高,权数的结构越复杂,但水远保持对称的权数,即两端项权数小, 一般系统的动态性 般说来历史数据对 平均作 去根据 的又商的次指敌平尚法和 3,1一次指数平滑法 L,预测模型 设时间序列为片,少,a为加权系数,0<口<1,一次指数平滑公式为 S,"=y,+(1-a)S9=Sg+ay,-S9) (13 式(13)是由移动平均公式改进而来的。由式(1)知,移动平均数的递推公式为 MM+ 以M四作为乃-w的最佳估计,则有 w-Mg+-为+-} 286
-286- clc,clear load y.txt %把原始数据保存在纯文本文件 y.txt 中 m1=length(y); n=6; %n 为移动平均的项数 for i=1:m1-n+1 yhat1(i)=sum(y(i:i+n-1))/n; end yhat1 m2=length(yhat1); for i=1:m2-n+1 yhat2(i)=sum(yhat1(i:i+n-1))/n; end yhat2 plot(1:21,y,'*') a21=2*yhat1(end)-yhat2(end) b21=2*(yhat1(end)-yhat2(end))/(n-1) y1986=a21+b21 y1987=a21+2*b21 趋势移动平均法对于同时存在直线趋势与周期波动的序列,是一种既能反映趋势变 化,又可以有效地分离出来周期变动的方法。 §3 指数平滑法 一次移动平均实际上认为最近 N 期数据对未来值影响相同,都加权 N 1 ;而 N 期 以前的数据对未来值没有影响,加权为 0。但是,二次及更高次移动平均数的权数却不 是 N 1 ,且次数越高,权数的结构越复杂,但永远保持对称的权数,即两端项权数小, 中间项权数大,不符合一般系统的动态性。一般说来历史数据对未来值的影响是随时间 间隔的增长而递减的。所以,更切合实际的方法应是对各期观测值依时间顺序进行加权 平均作为预测值。指数平滑法可满足这一要求,而且具有简单的递推形式。 指数平滑法根据平滑次数的不同,又分为一次指数平滑法、二次指数平滑法和三 次指数平滑法等,分别介绍如下。 3.1 一次指数平滑法 1.预测模型 设时间序列为 y1, y2 ,L, yt ,L,α 为加权系数,0 < α < 1,一次指数平滑公式为: (1 ) ( ) (1) 1 (1) 1 (1) 1 (1) t = t + − t− = t− + t − St− S αy α S S α y (13) 式(13)是由移动平均公式改进而来的。由式(1)知,移动平均数的递推公式为 N y y M M t t N t t − − − = + (1) 1 (1) 以 (1) Mt−1作为 t N y − 的最佳估计,则有 (1) 1 (1) (1) 1 1 (1) 1 1 − − − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = + − − = + t t t t t t M N N y N y M M M

令a=,以S代替M”,即得式13) S"=+1-a)Sg 为进一步理解指数平滑的实质,把式(13)依次展开,有 S"=a,+(1-a)[gy,a+(1-a)S8]=.=a∑1-a)/y,- (14) (14)式表明S四是全部历史数据的加权平均,加权系数分别为 a,a(1-a),a1-a)2,.;显然有 a1-ay=1-0-a =1 =S9 y,+(1-a) (15) 也就是以第 折数平滑值作为1+1期预测值。 加权系数的选择是很重要的 的 就愈大,原预测值所古的比重就愈小,反之亦然。若把式(15)改写为 (16) 则从上式可看出,新预测值 根据预测误差对原预测值进行修正而得到的。α的大小 则体现了修正的幅度,α值愈大,修正幅度愈大:口值愈小,修正幅度也愈小。 若选取α=0,则立=乃,即下期预测值就等于本期预测值,在预测过程中不考 虑任何新信息;若选取=1,则乃1=y,即下期预测值就等于本期观测值,完全不 去的1 角的 的具何 应根 能包今较长 h 则a应取 在实用上,类似移动平均法,多取几个α值进行试算,看哪个预测误差小,就采 用哪个。 3.初始值的确定 用一次指数平滑法讲行预测,除了选择合话的仪外。还要确定初始值s。初始作 测者估计或指定的 时间序列的 刃始值对 的 选 据较多比如在20个以上时 果时 时以后 就必须认 确定初 一般以最初几期实际值的平均值作为初始值 例4某市1976~1987年某种电器销售额如表4所示。试预测1988年该电器销售 -287
-287- 令 N 1 α = ,以 St 代替 (1) Mt ,即得式(13) (1) 1 (1) (1 ) t = t + − St− S αy α 为进一步理解指数平滑的实质,把式(13)依次展开,有 ∑ ∞ = = + − − + − − = = − − 0 (1) 1 2 (1) (1 )[ (1 ) ] (1 ) j t j j t t t t S αy α αy α S L α α y (14) ( 14 )式表明 (1) St 是全部历史数据的加权平均,加权系数分别为 α,α(1−α),α(1−α) 2 ,L;显然有 ∑ ∞ = = − − − = 0 1 1 (1 ) (1 ) j j α α α α 由于加权系数符合指数规律,又具有平滑数据的功能,故称为指数平滑。 以这种平滑值进行预测,就是一次指数平滑法。预测模型为 (1) 1 ˆt St y + = 即 t t t yˆ y (1 ) yˆ +1 = α + −α (15) 也就是以第t 期指数平滑值作为t +1期预测值。 2.加权系数的选择 在进行指数平滑时,加权系数的选择是很重要的。由式(15)可以看出,α 的大 小规定了在新预测值中新数据和原预测值所占的比重。α 值越大,新数据所占的比重 就愈大,原预测值所占的比重就愈小,反之亦然。若把式(15)改写为 ˆ ˆ ( ˆ ) t 1 t t t y = y + y − y + α (16) 则从上式可看出,新预测值是根据预测误差对原预测值进行修正而得到的。α 的大小 则体现了修正的幅度,α 值愈大,修正幅度愈大;α 值愈小,修正幅度也愈小。 若选取α = 0 ,则 t t yˆ yˆ +1 = ,即下期预测值就等于本期预测值,在预测过程中不考 虑任何新信息;若选取α = 1,则 t t y = y +1 ˆ ,即下期预测值就等于本期观测值,完全不 相信过去的信息。这两种极端情况很难做出正确的预测。因此,α 值应根据时间序列 的具体性质在 0~1 之间选择。具体如何选择一般可遵循下列原则:①如果时间序列波 动不大,比较平稳,则α 应取小一点,如(0.1~0.5)。以减少修正幅度,使预测模型 能包含较长时间序列的信息;②如果时间序列具有迅速且明显的变动倾向,则α 应取 大一点,如(0.6~0.8)。使预测模型灵敏度高一些,以便迅速跟上数据的变化。 在实用上,类似移动平均法,多取几个α 值进行试算,看哪个预测误差小,就采 用哪个。 3.初始值的确定 用一次指数平滑法进行预测,除了选择合适的α 外,还要确定初始值 (1) 0 s 。初始值 是由预测者估计或指定的。当时间序列的数据较多,比如在 20 个以上时,初始值对以 后的预测值影响很少,可选用第一期数据为初始值。如果时间序列的数据较少,在 20 个以下时,初始值对以后的预测值影响很大,这时,就必须认真研究如何正确确定初始 值。一般以最初几期实际值的平均值作为初始值。 例 4 某市 1976~1987 年某种电器销售额如表 4 所示。试预测 1988 年该电器销售 额
解采用指数平滑法,并分别取a=0.2,0.5和0.8进行计算,初始值 ”=51 即 =0=51 按预测模型 y.=ay.+(1-)y 计算各期预测值,列于表4中。 表4某种电器销售额及指数平滑预测值计算表(单位:万元) 年份 实际销售额y 预测值 预测值), 预测值, a=02 a=0.5 =0.8 50 303 198 0 4 68 01 从表4可以看出,《=0.2,0.5和0.8时,预测值是很不相同的。究竟《取何值为好, 可通过计算它们的预测标准误差S,选取使S较小的那个α值.预测的标准误差见表5。 表;预测的标准误差 45029 45908 计算结果表明:α=0.2时,S较小,故选取位=0.2,预测1988年该电器销售额 为,=51.1754 计算的MATLAB程序如下: clc.cle load dianqitxt%原始数据以列向量的方式存放在纯文本文件中 yha((((alpha) for i=2:n yhat(,i.片-alpha*y-IHl-alpha).yhat(-il,方 end vhat .1m-yha,2 yhat1988=alpha*yt(n)+(1-apha)*yhat(n.) -288-
-288- 解 采用指数平滑法,并分别取α = 0.2,0.5和0.8进行计算,初始值 (1) 1 2 0 51 2 y y S + = = 即 (1) 1 0 y S ˆ = = 51 按预测模型 1 ˆ ˆ (1 ) tt t y + =α y y + −α 计算各期预测值,列于表 4 中。 表 4 某种电器销售额及指数平滑预测值计算表 (单位:万元) 年份 t 实际销售额 t y 预测值 ˆ t y α = 0.2 预测值 ˆ t y α = 0.5 预测值 ˆ t y α = 0.8 1976 1 50 51 51 51 1977 2 52 50.8 50.5 50.2 1978 3 47 51.04 51.25 51.64 1979 4 51 50.23 49.13 47.93 1980 5 49 50.39 50.06 50.39 1981 6 48 50.11 49.53 49.28 1982 7 51 49.69 48.77 48.26 1983 8 40 49.95 49.88 50.45 1984 9 48 47.96 44.94 42.09 1985 10 52 47.97 46.47 46.82 1986 11 51 48.77 49.24 50.96 1987 12 59 49.22 50.12 50.99 从表 4 可以看出,α = 0.2,0.5和0.8时,预测值是很不相同的。究竟α 取何值为好, 可通过计算它们的预测标准误差 S ,选取使 S 较小的那个α 值。预测的标准误差见表 5。 表 5 预测的标准误差 α 0.2 0.5 0.8 S 4.5029 4.5908 4.8426 计算结果表明:α = 0.2 时,S 较小,故选取α = 0.2 ,预测 1988 年该电器销售额 为 yˆ1988 = 51.1754。 计算的 MATLAB 程序如下: clc,clear load dianqi.txt %原始数据以列向量的方式存放在纯文本文件中 yt=dianqi; n=length(yt); alpha=[0.2 0.5 0.8];m=length(alpha); yhat(1,1:m)=(yt(1)+yt(2))/2; for i=2:n yhat(i,:)=alpha*yt(i-1)+(1-alpha).*yhat(i-1,:); end yhat err=sqrt(mean((repmat(yt,1,m)-yhat).^2)) xlswrite('dianqi.xls',yhat) yhat1988=alpha*yt(n)+(1-alpha).*yhat(n,:)
32 当 间序 列的变动出现直线趋 势时, 法 后 线趋热植 势移动平均 滑,利用带后偏的规律建 滑法 S0=%,+1-a)S S2=aS0+(1-a)S (17) 式中S,为一次指数的平滑值:S,2为二次指数的平滑值。当时间序列y,},从某时 期开始具有直线趋势时,类似趋势移动平均法,可用直线趋势模型 iur =a,+bT,T=12 (18) 4=2S0-5,2 (5-) (19) 进行预测。 例5仍以例3我国1965~1985年的发电总量资料为例,试用二次指数平滑法预 则1986年和1987年的发电总量。 表6 我国发电总量及 二次指数平滑值计算去 (单位:亿度 年份 发电总量 一次平滑值 三次平滑值 的估计值 56 720 784.0 197 1150 786 8757 1972 967 13084 10 072 0 307 223 51 4107 036 3916.6 解取a=0.3,初始值S和S2都取序列的首项数值,即S=S=676。 计算S,S2,列于表6。得到 S"=3523.1,S2=3032.6 由公式(19),可得1=21时 -289
-289- 3.2 二次指数平滑法 一次指数平滑法虽然克服了移动平均法的缺点。但当时间序列的变动出现直线趋 势时,用一次指数平滑法进行预测,仍存在明显的滞后偏差。因此,也必须加以修正。 修正的方法与趋势移动平均法相同,即再作二次指数平滑,利用滞后偏差的规律建立直 线趋势模型。这就是二次指数平滑法。其计算公式为 (1) 1 (1) (1 ) t = t + − St− S αy α (2) 1 (2) (1) (1 ) St = αSt + −α St− (17) 式中 (1) St 为一次指数的平滑值; (2) St 为二次指数的平滑值。当时间序列{ }t y ,从某时 期开始具有直线趋势时,类似趋势移动平均法,可用直线趋势模型 yˆt+T = at + bt T ,T = 1,2,L (18) ⎪ ⎩ ⎪ ⎨ ⎧ − − = = − ( ) 1 2 (1) (2) (1) (2) t t t t t t b S S a S S α α (19) 进行预测。 例 5 仍以例 3 我国 1965~1985 年的发电总量资料为例,试用二次指数平滑法预 测 1986 年和 1987 年的发电总量。 表 6 我国发电总量及一、二次指数平滑值计算表 (单位:亿度) 年份 t 发电总量 yt 一次平滑值 二次平滑值 yt+1的估计值 1965 1 676 676 676 1966 2 825 720.7 689.4 676 1967 3 774 736.7 703.6 765.4 1968 4 716 730.5 711.7 784.0 1969 5 940 793.3 736.2 757.4 1970 6 1159 903.0 786.2 875.0 1971 7 1384 1047.3 864.6 1069.9 1972 8 1524 1190.3 962.3 1308.4 1973 9 1668 1333.6 1073.7 1516.1 1974 10 1688 1439.9 1183.6 1705.0 1975 11 1958 1595.4 1307.1 1806.1 1976 12 2031 1726.1 1432.8 2007.2 1977 13 2234 1878.4 1566.5 2145.0 1978 14 2566 2084.7 1722.0 2324.1 1979 15 2820 2305.3 1897.0 2602.9 1980 16 3006 2515.5 2082.5 2888.6 1981 17 3093 2688.8 2264.4 3134.1 1982 18 3277 2865.2 2444.6 3295.0 1983 19 3514 3059.9 2629.2 3466.1 1984 20 3770 3272.9 2822.3 3675.1 1985 21 4107 3523.1 3032.6 3916.6 解 取α = 0.3 ,初始值 (1) S0 和 (2) S0 都取序列的首项数值,即 676 (0) 0 (1) S0 = S = 。 计算 (1) (2) , St St ,列于表 6。得到 3523.1 (1) S21 = , 3032.6 (2) S21 = 由公式(19),可得t = 21时