
Multiplicative Inverses 【模的乘 法的逆】(1) The residues modulo a positive integer n are the set Zn={0,1,2,,(n-1)} Letx and y be two elements of Z,,such that xy mod n=1 We say thaty is the multiplicative inverse ofx in Z,and we writey=x ●Example: Multiplicative inverses of the residues modulo 11 X 0 1 2 3 4 5 6 8 9 10 七r1 1 6 4 3 9 2 8 7 5 10 3/31/2016 Cryptography 17
Multiplicative Inverses【模的乘 法的逆】 (1) The residues modulo a positive integer n are the set Zn = {0, 1, 2, …, (n - 1)} Let x and y be two elements of Zn such that xy mod n = 1 We say that y is the multiplicative inverse of x in Zn and we write y = x -1 Example: Multiplicative inverses of the residues modulo 11 3/31/2016 Cryptography 17 x 0 1 2 3 4 5 6 7 8 9 10 x -1 1 6 4 3 9 2 8 7 5 10

Multiplicative Inverses (2) Theorem An elementx of Z,,has a multiplicative inverse if and only if x and n are relatively prime ● Example The elements of Zio with a multiplicative inverse are 1,3,7,9 Corollary If is p is prime,every nonzero residue in Z,has a multiplicative inverse Theorem A variation of Euclid's GCD algorithm computes the multiplicative inverse of an elementx of Z,or determines that it does not exist X 0 1 2 3 4 5 6 7 8 9 七1 1 7 3 9 3/31/2016 Cryptography 18
Multiplicative Inverses (2) Theorem An element x of Zn has a multiplicative inverse if and only if x and n are relatively prime Example The elements of Z10 with a multiplicative inverse are 1, 3, 7, 9 Corollary If is p is prime, every nonzero residue in Zp has a multiplicative inverse Theorem A variation of Euclid’s GCD algorithm computes the multiplicative inverse of an element x of Zn or determines that it does not exist 3/31/2016 Cryptography 18 x 0 1 2 3 4 5 6 7 8 9 x -1 1 7 3 9
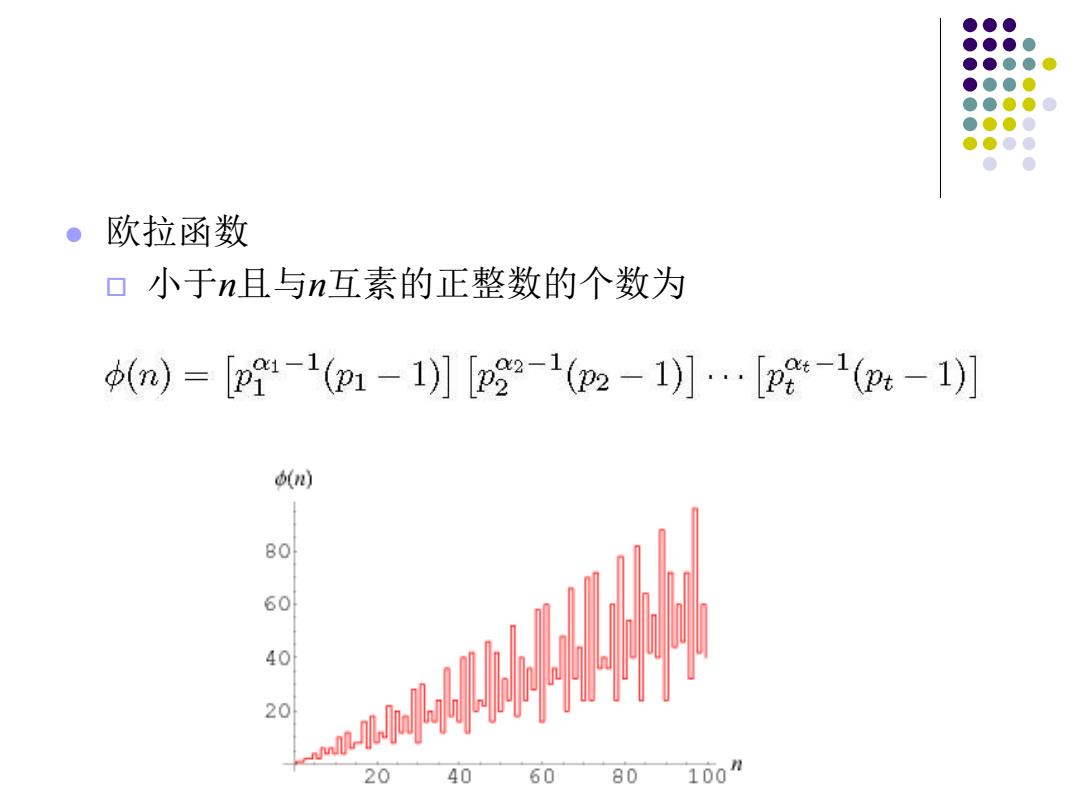
●欧拉函数 口小于n且与n互素的正整数的个数为 (n)=[1-1(m1-1】[2-1(2-1】…[2-1(px-1] d(n) 80 60 40 20 20 40 60 80 100n
欧拉函数 小于n且与n互素的正整数的个数为