
49 956 第四章频域图像增强 电子科技大学自动化学院
第四章 频域图像增强 电子科技大学自动化学院

目录 CONTENTS >傅里叶变换和频域介绍 >平滑的频域滤波器 >频域锐化滤液器 >同态滤波器 >选择性滤波* >傅里叶变换的实现
目录 CONTENTS 傅里叶变换和频域介绍 平滑的频域滤波器 频域锐化滤波器 同态滤波器 选择性滤波* 傅里叶变换的实现
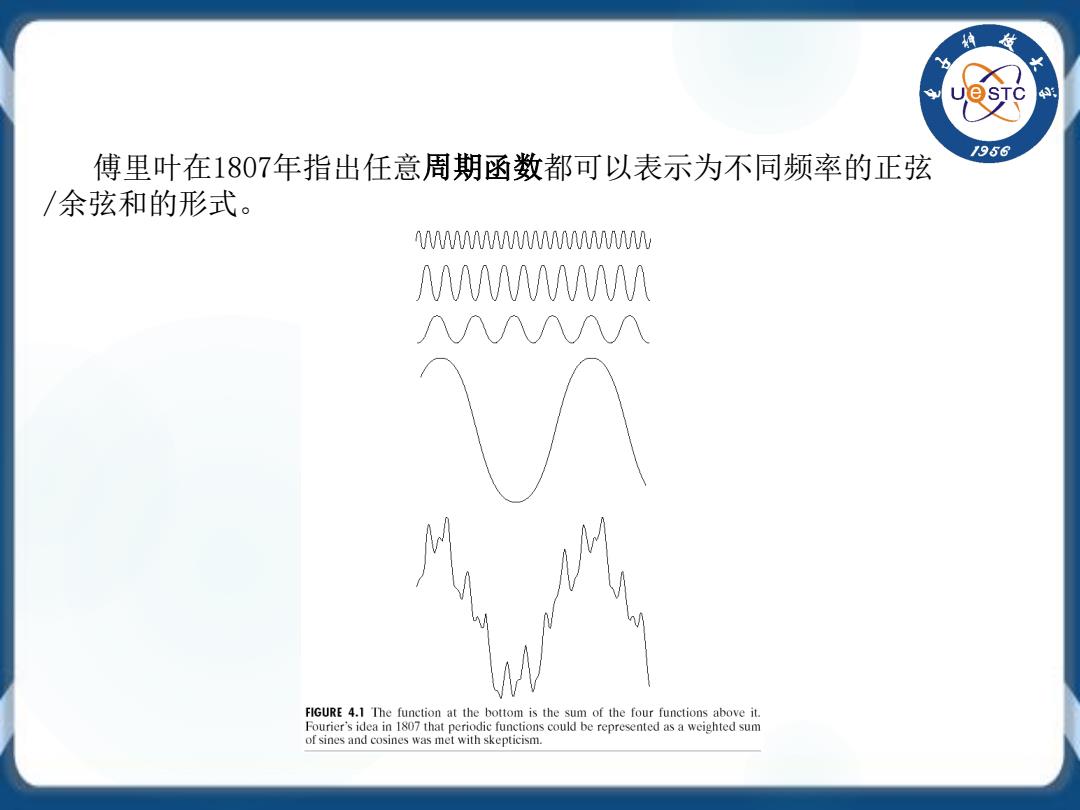
/956 傅里叶在1807年指出任意周期函数都可以表示为不同频率的正弦 /余弦和的形式。 N WWWM ∧AAAN FIGURE 4.1 The function at the bottom is the sum of the four functions above it. Fourier's idea in 1807 that periodic functions could be represented as a weighted sum of sines and cosines was met with skepticism
傅里叶在1807年指出任意周期函数都可以表示为不同频率的正弦 /余弦和的形式

4.1傅里叶变换和频域介绍 1956 一维傅里叶变换: F(u)=f(x)e-2me dx 一维傅里叶反变换: f(x)=F(u)eizmedu F(u)台f(x)
4.1傅里叶变换和频域介绍 一维傅里叶变换: 一维傅里叶反变换: F u f x e dx j2πux ( ) ( ) − ∞ ∫−∞ = f x F u e du j2πux ( ) ( ) ∫ ∞ −∞ = 𝐹𝐹(𝑢𝑢) ⇔ 𝑓𝑓(𝑥𝑥)

形式: 1956 M-1 F(u)= ∑f)e12mMu=0,1.2,…M-1 X=0 M-1 f(x)= F(u)ej2πx/Mx=0,1,2,…M-1 u=0 注意:正变换前的1/M,有时候放在反变换 前面,还有的时候分解为1/M,放在正反变 换前面。这并不影响问题的本质
形式: 注意:正变换前的1/M,有时候放在反变换 前面,还有的时候分解为1/ 𝑀𝑀,放在正反变 换前面。这并不影响问题的本质。 正变换: 反变换: 𝐹𝐹(𝑢𝑢) = 1 𝑀𝑀 � 𝑥𝑥=0 𝑀𝑀−1 𝑓𝑓(𝑥𝑥)𝑒𝑒−𝑗𝑗𝑗𝑗𝑗𝑗𝑗𝑗𝑗/𝑀𝑀𝑢𝑢 = 0,1,2, ⋯ 𝑀𝑀 − 1 𝑓𝑓(𝑥𝑥) = � 𝑢𝑢=0 𝑀𝑀−1 𝐹𝐹(𝑢𝑢)𝑒𝑒𝑗𝑗𝑗𝑗𝑗𝑗𝑗𝑗𝑗/𝑀𝑀𝑥𝑥 = 0,1,2, ⋯ 𝑀𝑀 − 1