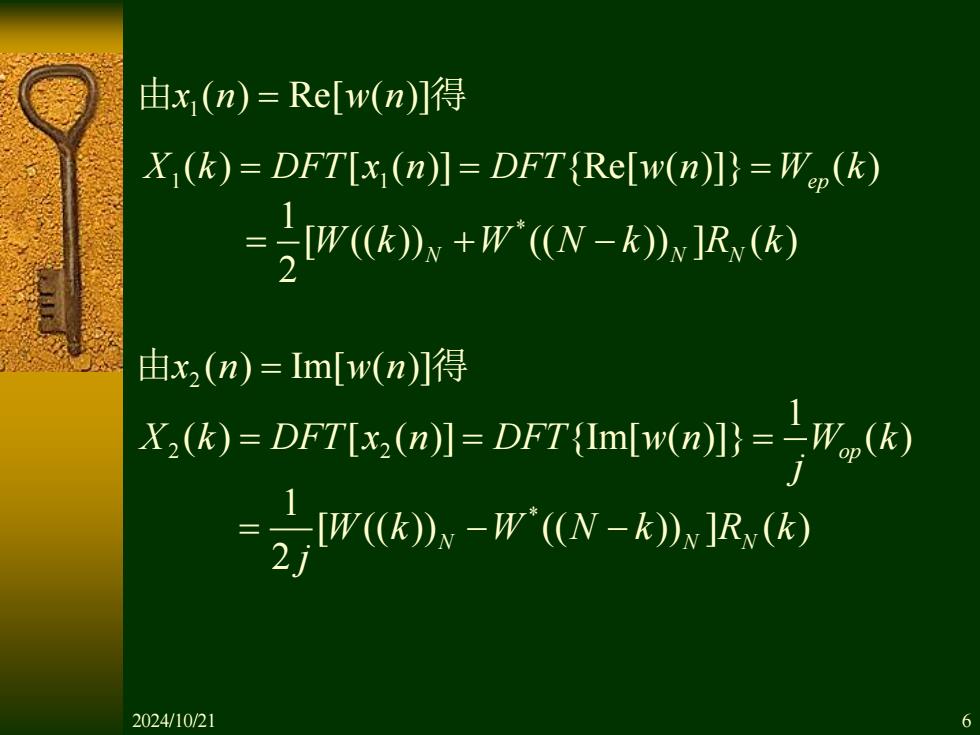
由x,(n)=Re[w(n)]得 X (k)=DFT[x (n)]=DFT{Re[w(n)]=W(k) =2(》+W(V-,]R( 由x2(n)=Im[w(n)]得 X:(k)-DFTl:()-DFT{Iml(() 子》.-g-.R因 2024/10/21
1 由 得 x n w n ( ) Re[ ( )] = 1 1 ( ) [ ( )] {Re[ ( )]} ( ) X k DFT x n DFT w n W k = = = ep 1 * [ (( )) (( )) ] ( ) 2 = + − W k W N k R k N N N 2 由 得 x n w n ( ) Im[ ( )] = 2 2 1 ( ) [ ( )] {Im[ ( )]} ( ) X k DFT x n DFT w n W k op j = = = 1 * [ (( )) (( )) ] ( ) 2 W k W N k R k N N N j = − − 2024/10/21 6

解:由题意X(k)=DFT[x(n)],Y()=DFT[y(n)] 构造序列Z(k)=X(k)+Y() 对Z(k)作一次V点FFT可得序列(n) E(n)=IDFT[Z(k) 又根据DFT的线性性质 =(m)=IDFT[Z(K)]=IDFT[X(k)+jY(k)] IDFT[X (k)]+jIDFT[Y (R)] =x(n)+y(n) 而x(n),y(n)都是实序列 x(n)=Re[z(n)] y(n)=Im[=(n)] 2024/10/21
解:由题意 X k DFT x n Y k DFT y n ( ) = = ( ) ( ) ( ) , 构造序列 Z k X k jY k ( ) = + ( ) ( ) 对 Z k( ) 作一次N点IFFT可得序列 z n( ) 又根据DFT的线性性质 = + IDFT X k jIDFT Y k ( ) ( ) 而 x n( ) , y n( ) 都是实序列 ( ) ( ) ( ) ( ) Re Im x n z n y n z n = = z n IDFT Z k ( ) = ( ) z n IDFT Z k IDFT X k jY k ( ) = = + ( ) ( ) ( ) = + x n jy n ( ) ( ) 2024/10/21 7