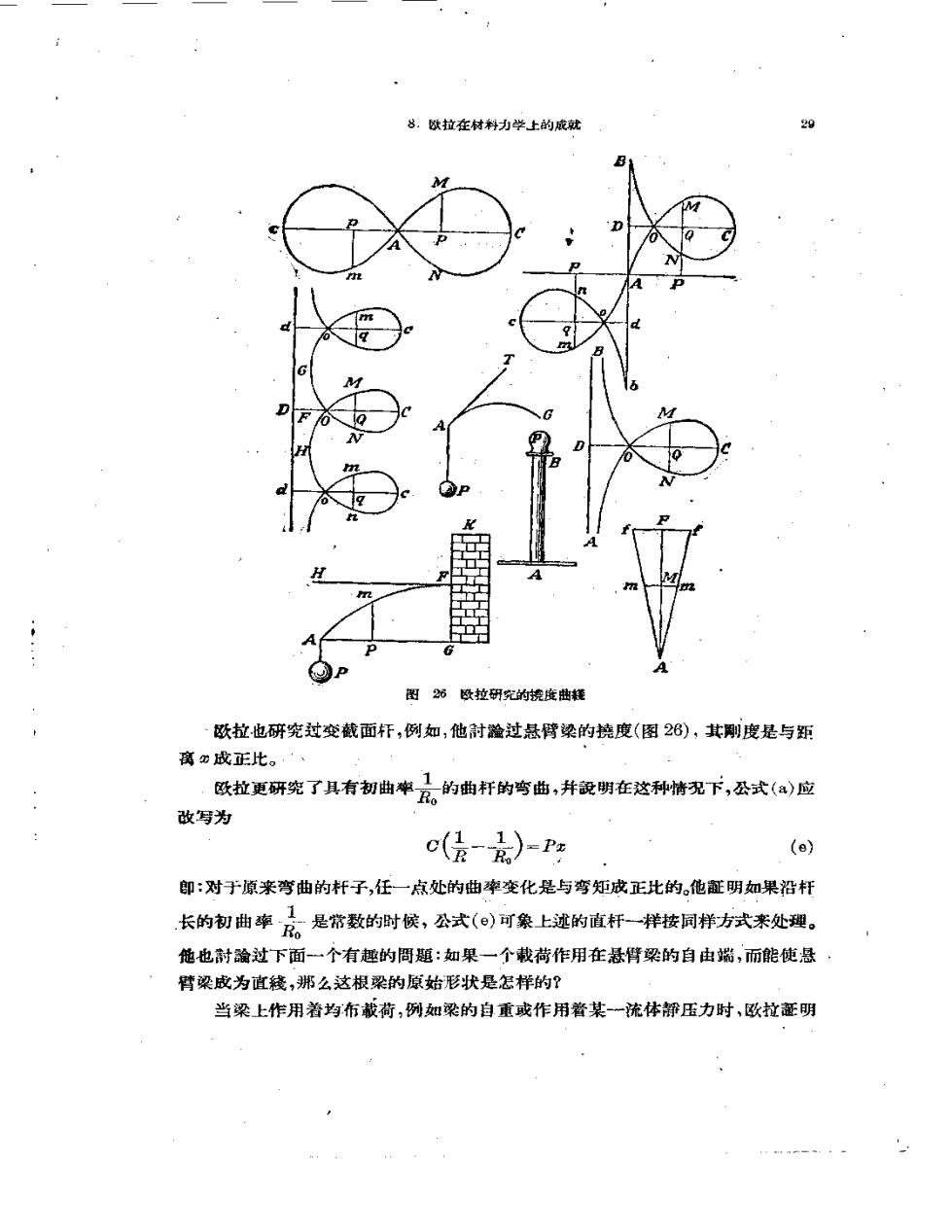
8.做拉在材料力学上的成就 29 图6欧拉研究的烧度曲耗 欧拉也研究过变藏截面杆,例如,他討脸过悬臂梁的撓度(图26),其刚度是与跖 商心成正比。,·、 欧拉更研究了具有初曲率品的曲杆的弯曲,并设明在这种情无下,公式(®)应 改写为 c(层-嘉)=P ()》 即:对子原来弯曲的杆子,任一点处的曲率变化是与弯矩成正比的。他証明如果沿杆 长的初曲率亮是常数的时候,公式(。)可象上速的直轩一样按同榉方式素处理。 他也耐論过下面一个有趣的周题:如果一个截荷作用在悬臂梁的自由端,而能使悬· 臂梁成为直袋,哪么这根梁的原始形状是怎样的? 当梁上作用着均布截荷,例如梁的自重或作用者某一流体都压力时,欧拉証明

吃 第二璩性曲疑 罪性曲钱的微分方程将是一个四灰方程。他成功地解出在水静压力情孔下的这个 方程,井且得出用一个代数式表示的撓度曲线。 在政拉的著作中,我們更可看到他对于杆的横向振动的研究。在限于討韵小 挠度的情乳下,他藏,他能取器作为梁孩携曲后的曲率、照现用曲镜方程式一样 的形式写出曲钱的微芬方程。为了消除重力的影响,他假定振动杆AB是垂直地 嵌人于A端(图7a),然后考察具有重量心的徽芬元素mm的运动。他覌測到 这种运动和商单等时摆(图27b)的运动完全相 同,且使此元来拉向x軸的力也一定和摆相 同,卸在极小振动之下,它将等于侧。欧拉 解释其理由是:“如果对板条的单独元素n, 在对立的方向(在y轴方向上)加上相等的力 y光,即在AmnB位置处的板条会保持不衡 Wdx 状态。因此,此板条在板动时的曲率可乱为与 图27 茲板条处于静止时在各个元素mm上作用着y 方向的力叫警所具有的由率相同”。这样,欧拉得出的黏论正和我们现在用达 朗伯D')原理所得的相同以。知道了分布鞍荷后,欧拉将C器-M微 分两次便得出所求的运动微分方程,井猊察到M的二次导数和横向截荷的集度是 相等的,即: c器竖 () 于是欧拉得出钻論:“因此,利用这个方程就可以把曲後AmB的特征装示出来, 而且,若所给的条件为已知时,由它就可决定长度工(当量摆的长度)。如果摆长为 已知,即其本身的振动也可以将它决定出来”。接着他将公式()积分,并利用板条 蜡部的假設条件求得頻华方程式,从類犁方程式便能計算一速串振动方式的頻孳。 欧拉不但分析了悬臂梁,他也制論到下面-一些杆件的横向运动:(1)两端簡支 的,(2)两端固定的,以及(③)两端完圣自由的。对于所有各种情况,他建立了計算 頻率的公式 f=m√/红O2 (g) wl [1]达朝伯著“动力学验装”(Tri伦de Dynamique),1743,但当政拉写出他的书“变牙法”(Mietho- dna1nve如iendi.,)的附录“排性曲镜”(Do Curvig Elasticis)时还没有者到这本书a

9.拉褚期日 81 式中为一常数,視杆端搁置情况以及振动方式面定。在轱論中,欧拉說明了公 式(g)不仅能应用它来校核他的理欲,而且也可实地用来决定此板条的“絕对彈性” C的值 1767年,欧拉再出版了关于柱压屈閏題的书“。在书中他利用豁过蘭化的微 分方程。=一Py簡单地导出了临界戴荷的公式。他在这里更群糊而正确地 衬論了心的数值,并月断定它必須是力的因次乘以长度的平方。在以后的验文中, 欧拉将他的芬析推到变截面柱,而且也研究了具有沿长度分布的轴向戴荷的压 杆問題,不过他对于这些較复杂問題井沒有得出正确的懈式。 雅斯奎士·伯諾里(Jacques Bernoulli,1759~1789)a,提到过欧拉的舱文“关 于作用在-块平校表面上一个集中荷重的压力”(Von de如n Drucke eines mit einem(ewichte beschwerten Tisches auf eine Flaeche),其中第一次提到超靜 定的問题。这是根据板的頂面保持平面的假定解出来的。 欧拉也惧进了完圣柔性膜的撓曲与振动的理输。制为膜是两粗互相直交的索 子所組成的,他导出偏微分方程的 器-e器+6 这个概念以后为推斯奎士·伯諾里所引用,当他研究一块矩形板的弯曲和振动时, 會认定板为两个梁系所粗成的格构面得出下面的方程【1: 他用这个方程米說明施拉德尼(E.F.F,Chladni)对于板振动的实验桔果(参看 第29节)c 9.拉格期日(Lagrange,1736~1813) 拉格朗日出生于都灵(Irn,意大利西北地名一譯者注)o。他的父亲原是 一个富翁,在几次投机生意失敗之后,財产損失迨尽。青年的拉格朗日后来款为 [J们見柏林科学院研究报告“关千柱的承枪力”(Snr1 a force dee Colonnea),fem.Acad,Berlin, 13卷,1759。 E]丹尼尔·伯诺里的侄儿。他溺死在尼瓦河(N®a River)中。 ]見被得科学跷会报(Novi comm,Acad.Pet立op.)10磨,248真,1767。欧拉宋用这-含求 研究怡的:动(参看同-一清作,261瓦)。 [4]見“新論”(心ova act)卷5,1750,圣彼得堡。 [5]见达南布留(J.B.J.Delamhre)著放摇朗日的,拉格明日的成就”(0 ouvres d6工agrange) 卷寸,187,巴聚

32 第二章彈性曲袋 失去财产是有补偿意义的,因为假使他家还是很富有,他就不会去研究数学了。他 很早就表現了特殊的数学才能,在十九岁时巳成为都灵皇家炮兵学校(Roya1 Artillery School)的数学教授了。 他邀集許多学生粗辙了一个学会,以后便成为都灵科学院。在这个学会的第 一期刊物中(1759年发行),刊出了好几篇拉格 朗日的究报出、这些研究报告成为他在变分 法上的重要貢献,由于这方面的共同兴趣,他 和欧拉經常通信。欧拉非常佩服拉格朗日的成 就,因此推荐他为柏林科学院的国外会員,在 1759年正式通过。1766年由于欧拉和达朗路 尔两人的推荐,聘他为骸院接替欧拉的人,于是 他搬到柏林。在柏林他得到关好的工作环境, 不久就发表了一系列的重要論文。 在这个时期中,他还写成了著名的“力学分 析”(Mecanique Analytique)。书中拉格朗H 用了达朗培尔原理和虚位移原理引出了“ 图28J.L.拉格朗日 义坐标”(generalized coordinates)和“广义力” (generalized forces)这两个新的概念,并且将力学理腧归钢为某些一般公式,从这 些公式中,任何特殊問题所需的方程都能推导出来。在序言里面,拉格朗日說明他 的书里沒有插图,因为他所宋用的方法并不需要作几何学或力学方面的研討,只是 娑照规定的永序作出一些代数运算而已。在拉格朗日的掌握下,力学变成了解析 法的一分支,他称之为“四雉几何(geometry of four dimensions)。挪时,能賞識 这种力学表示方法的人为数很少,因此拉格朗日很难找到出版商来出版他的著作。 这本书終于在1788年在巴黎出:版,但已經落后于牛頓刊行“物界原理'(Prineipia) 一百年之久了。 腓特烈二世(Frederick the G江eat)死后,柏林的科学研究条件日趋低落,拉格 朗日威到不能象以前那样受到拿重了,因之在1787年他搬到巴黎。在法国首都他 受到热烈欢迎,他住在卢夫宫(Louvre),照常度着他的榆快生活。由于工作繁重 的結果,拉格朗日完全失去时間来关心数字的研究,大概有两年光景,他那本已出 版的“力学分析”一直沒有理会过它。在这段时間内,他关心了其他的-…些科学,特 别是化学,并且参加了討詒法国乐用米制的委員会的工作。 这时,正当法国革命,拉格朗日打算离开法国。可是在那时有一一所新学

8.拉格明日 88 校-一工业学院(cole Polytechnique)开办了,拉格朗日被聘到这所新学校新授 积分学。这才使他重新恢复对数学的关心,他的就演不独吸引了学生們,而且还有 許多教师和教授們。作为这些耕授的成果,他号出了两本书:“解析函数'(Fonctions analytiques)和“数值方程解法”·(rait(de la Resolution des eq卫ations numeriques)。在他险死前几年中,他从事于打正他所著的力学,但在他18们3年 去世时,这一项工作只完成了三分之二。修版的第二卷到他死后才发行。 拉格朗日在强性曲籁上最重要的成就是他的研究报告“柱的形状”(s口r丸 五gure des colonnes)u。他首先射胎一根两端饺接的棱柱杆(图29),持假定在軸 句压力P作用下骸杆已产生徽小的将曲。这使他想到欧拉老早衬龄过的方程(叁 看上节) y=-Py (a】 他指出此方程的解为y=可咖√侣,只在√牙: P x时亨满足端部条件,其中m为一整数。由此可 知,能使压杆发生微小弯曲时所支承的截荷可用下式 表示 P=mπ0 (a) (b) (b) 图29 因此可能会有-一个无穷数的压屈曲线。要产生如图29所示的、具有半波的曲凝, 我們必須用一个大到欧拉对一端固定情况下所算出的四倍的截荷。要得出如图 29畅所示的曲後,所需截荷应为欧拉所得出的十六倍,其余恢此类推。拉格朗日不 只限于算出载荷P的临界值,而且进一步研究了当栽荷P超过临界值时所将发生 的撓曲。为此,他朵用包含有曲率的精确表示式的方程来代替式(a)的近似方程, 展成极数后进行积分,得 1-1++o两+0两+-] 9.25P3f9 Wō 当f=0时,此方程得出公式()。当f值甚小时,此殺数收敏极快,相应于已知撓 度的载荷是很容易計算出来的。 接着,拉格朗日研究变截面柱(柱为轉成体),井探耐如何决定一根曲钱,使它 繞一轴阿轉时能得出具有最大效李的柱的外形。拉格朗日取用了临界载荷P对柱 1门覓达南布需(.B.↓,Dalembre)著,“拉格朗H的成就”(0emvr阳d0 Lagrang0)磨2,125食: