
6.照里沃特 19 波义耳-馬里沃特定律,此定律說明了在温度不变的情况下,一定质轻的气体其压 力与体积的相乘积保持不变。 在固体力学方面,馬里沃特創立了神击定理,他利用悬挂在蝇索上的小球来說 明动最守恒。他发明了冲击摆。 i 思里沃特在一篇流体运动的驗文山里包括了他对琿性力学方面的研究。他信 設計过通向凡尔塞宫的一条供水管镜,設的結果使他对于梁的抗弯强度发生了 兴趣。利用木杆和玻璃杆做实驗,他发現加利略理翰所得的断裂截荷值过大,因之 提出了他自己的弯曲理論,在他的理验中已将材料的理性考虑在内。 他作了簡单拉伸武验。图20a1表示在他的木材拉伸试驗中所朵用的装置方 法。图20b中表示轹的拉伸武驗。馬里沃特不独重靓材料的絕对强度,而且也重 魂它的彈性,他发現在所有试驗过的材料中,其伸长盘与所加的力成正比。他說 明当伸长量超过某一极限时材料便发生断裂。在他討論悬臂梁的弯曲时(参看图 图20鹏里沃特所作的拉伸与弯曲武输 []这簪徐文在1686年馬里沃特荆去世不久由海日(M.de1 Hire)将生出殷。并参君馬里沃特第 子第二卷,1740,燕牙刊第二版。 [2]图即是从馬里沃特文掩中取用的

20 第一章于七世纪中的材科力学 20c),他首先考察支于0点处的一根杠杆AB(图20)的本衡。'在杠杆的左臂上, 挂上三个等截荷G-H=I=I2謗,离芬别为AC=4呎,DC=2呎,0=1呎, 为了平衡它們,在C=12呎处加土戟荷F,必須使F-7磅。.假骰将载荷F婚 大宵許,杠杆将德C点旋轉。A,D及E各点的位移将与离C点的距离成正比,但 加在那些点上的力仍等于12磅。現在考察同样的杠杆,但假定截菏G,丑,王用三 根同样的金展絲D.r,GL,HM(图20e)来代替,金属稀的絕对强度等于1之磅。 、在計算使各金凤铩发生断裂的栽荷B时,馬里沃特規察到当金属繇DI所受的力 到达极限值12蘅时,G工和HI两根金風耕所受的力与各自的伸长量成比例将 分别为6磅及3磅,因之极限载荷R只为51/2磅,而不是和前逃情况中一样的 T磅。 馬里沃特用同一理論来研究悬臂梁的弯曲(图20)。假定在撕裂时梁的右面 一段襪D点旋轉,他的結論是:在其叙向新雜中所受的力与其去D的距离成同祥的 比例,由此可見,在一根矩形梁的情况下,这些力的总和将等于S2(即梁的絕对强 瘦只有一军受拉力,而且它付对D的力娅将是昌×登A一密,式中么为梁的离 度。将此值与所加载荷L的力矩九列成等式,即可求出极张裁背为 1=欲 (a) 因此,将符雜的变形考虑进去,井且和加利略所做过的一样,利用同一旋轉点D,馬 里沃特求出弯曲的极限截荷工与絕对强度S之比等于.(五/3):。这就說明了极限 截荷只等于加利路所算得的钻果之2/3。 接着馬里沃特进行了更进一步的分析,仍然引用上述的矩形梁(图20),他鸡 察到横截面下面部分ID的舒雉是压縮状态,而上面部分IA的符维呈拉伸状态。 他朵用公式(a)来計算克服受拉符維的抗力所需的载荷工,井将五/2代替五,得出 五0 (b) 关于横截面下面部分ID的受压新摊,·馬里沃特假設受压时力的分布定律地和受 拉的情况相同,而且极限强度也相同。因此,由受压轩傩形成的梁的强度其作用也 将等于L,如公式(b)所示。总强度则如上递公式(⑧)所示。在馬里获特的分析 中,我們肴到他在彈性梁内所用的应力分布理豁是很适当的。他那关于新維中应 力分布的假設地是正确的,不过在引算对于I点的拉力力矩时,不仅要用乃/2代替 (a)式中的五,而且也要用S2代替式中的S。这个结使得馬里沃特不能对材料 服从于虎克定律直到断裂为止的梁作出計算梁断裂的正确公式

5.馬風沃特 21 为了証明他的理脸,馬里沃特用直徑为1/4时的木質圓杆作过实驗。由拉伸 武驗得出絕对强度为S=330磅。将此杆作为长度L✉4时的悬臂梁1来武险,他 求出极根較荷乙一6请,得受-5,但由丞式(®得出艺-4间,而由加利路理路 却得出号-32。馬里沃特企图解释他的实验精果不能与公式(®)的計算特果相符 是由于“时間效应”之故。他說,受拉武件在截荷300膀作用下如果截荷作用时固 很长,則裂口将裂开得更大。当他用玻璃杆重复实驗后,馬里沃特再发现到用他的 公式(a)算出的数值比加利略所得出的要精确得多。 这位法国物理学家也信用两端支承的梁进行过武驗,他发现两端固定的梁所 能负裁的中央截荷的极限值較之同样尺寸的簡支梁所负截的大出1倍。 利用一系刻有趣的武驗,馬里沃特发现了在水静压力作用下管子抵抗服裂的 强度,为此目的,他用一个圆柱形桶AB(图21),桶上接速一根 垂直的长管子。将水注人管子和桶中去,使管中水面高度逐撕 升高1,最后它能使桶限裂。用这样方法他断定了管壁所需厚 度必須与内压力以及管的直徑成正比。 在处理方形板受均布截荷的弯曲时,里沃特根据同样的 研究,正确地确定了如果厚度完全相同,則板上总的极限截荷将 图21鹏里沃特 保持定值,而与极的大小无关。 作服婴武喻所用的 在这里我例可以看到馬里沃特大大地丰富了彈性体的力学 图挂彩桶 理脸。由于提出了考忠球性变形的結果,他故进了梁的弯曲理龄,井利用实驗来校 核他的假競。他用实驗校正了加利略关于“梁的强度随跨长而变更这方面的一些 結舱。他研究了将梁的两端固定后对梁的强度的效应,并且得出管子脹裂强度的 公式。 [1]馬里沃特在他的胎文中提到这些式验是在罗伯佛(Roberval)和度夸斯(Huyghens)两位在援时 欧出来的。 [2]注意公式()是从矩形酸面粱推导出的,而思里沃特将它用到圈形截面粱。 [3]在这些武验中,水头接近100职

第二章 彈性曲綫 6.数学家伯諾里(Bernoulli)山 伯諾里的家族原先住在安特韦普(Antwerp,原属荷兰現属比利时一譯者 注),因受阿尔巴(A1ba)公爵的宗教迫害,他們才离开荷兰,在十六世紀末叶搬 到巴塞尔(B$ol,瑞士地名,临近德、法两国。一譯者注)安家立亚。从十七世 紀未叶起将近一百年中这一族出过一些出色 的数学家。1699年,法国科学院选举了雅可 普·伯諾里(Jacob Bernoulli)和約翰·伯諾里 (John Bernoulli)两兄弟为外籍会員,直到 1790年,这个組辙里面总有他們这一族的典型 人物叁加。 十七世紀的最后二十五年到十八世紀的开 初,微积分学开始迅速地发展。最初是由欧洲州 大陆的莱布尼茲(Leibnitz,1646~1716)开 始的,而主要的发展还是雅可普·伯諾里和約 翰·伯諾里两兄弟的功績。为了扩展此种新数 图22雅可普·伯蕾里 学的应用范图,他俩討論过許多力学和物理学 上的例题。有一个例题是由雅可普·伯蒂里(1654~1705)提出来的1卸关于彈性 杆撓度曲筏的形状,从此他开創了彈性体力学中重要的一章。其实,加利略和馬 [I]关于他的佛配,可允彼得·麦里安(Peter Merian)著:“数学家伯带里”(Die Mathematiker Pernoulli),1860,巴塞尔。 [2]在英国牛傾独立地发展了积分原理,但在欧洲大陆上葵布尼兹的表示方法及其配数法在这門数学 的迅速成长中已被朵用。 [3]經过1694年出版的莱布尼兹所著“利普获学者的功锁”(Acta Eruditorum Lipsiae)一书对此 周题作出一些初步莳論之后,位将饱对此周题的最后兒解刊入“巴黎科学院史”(Histoire de1'Aed6mie des cien(ces de Paris),1705。并台君“雅可迹·伯箭里的验文”(Cllected Works of J,Bernoulli) 2卷,9?G宜,1744,日内瓦
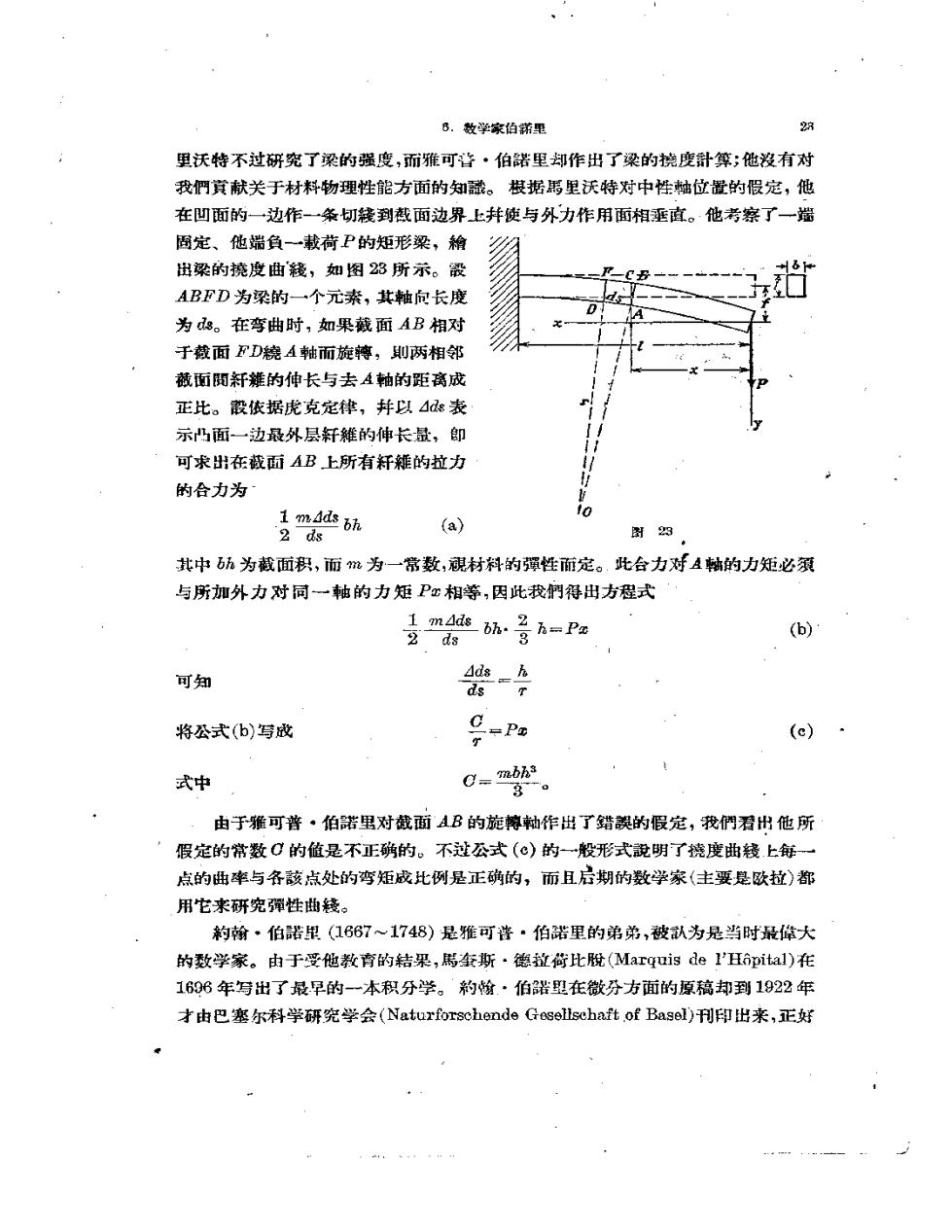
B.数学家伯薪里 28 里沃特不过研究了梁的强度,而雅可普·伯器里却作出了梁的撓度計算;他沒有对 我們買献关于材料物理性能方面的知識。根据馬里沃特对中性轴位置的假定,他 在凹面的一边作一条切餐到截面边界上井使与外力作用面相垂直。他考察了一瑞 固定、他端负一載荷P的矩形梁,棉 出梁的撓度曲袭,如图23所示。最 ABFD为梁的一个元素,其軸向长度 为。在弯曲时,如果截面AB相对 于载面FD繞A轴而旋幕,即两相邻 藏面閱籽雜的伸长与去A轴的距离成 正比。皲恢据虎克定律,并以4表 示凸面一边最外层轩雉的伸长景,即 可求出在截面AB上所有籽雜的拉力 的合力为 imAds bh 0 2 ds (a) 图23 其中h为截面积,而m为一常数,魂材料的镯性而定。.此合力对A軸的力矩必须 与所加外力对同一轴的力矩P:相等,因此我們得出方程式 1m4a8M: 五=Pe (b) 可知 Ads ds 将公式(b)写成 CPa (c) 式中 C=mbha 3。 由于雅可普·伯諾里对截面AB的旋韓轴作出了错美的假定,我們看州他所 假定的常数C的值是不正确的。不过公式(心)的一般形式說明了糖度曲钱.上年一 点的曲率与各骸点处的弯矩成此例是正确的,而且后期的数学家(主要是欧拉)都 用它来研究彈性曲钱。 钓瀚·伯諾里(1667~1748)是雅可谐·伯諾里的弟弟,被款为是当时最降大 的数学家。由于受他教育的结果,馬奎斯·德拉荷此脫(Marquis de1'H6 pital)在 1696年写出了最早的-一本积分学。'的愉.·伯器盟在微牙方面的原稿却到1922年 才由巴塞尔科学研究学会(Naturforschende Gesellschaft of Basel)刊印出来,正好