
1.加利略 坎尼(Tuscany,意大利西部地.名,譯者注)公爵那里。1610年9月他商开拔都仍 回到佛罗倫薩。在他的新职位上,除了继;他的科学研究之外,沒有别的任务。他 以全部精力投入于天文学的研究中。他发現了土星特有的形状,观察到金星的相 位井描迹了太阳上的黑子。 所有这些光辉的发现以及他热心于写作支持哥白尼理論的文章引起了教会的 注意。他們将他邪行星系的新覌点和圣經上覌点之間的矛盾提付审問,在1615年 加利略接到牛官方的警告,要他迴避神学,而只限于作物理的論証。1616年,哥白 尼的偉大著作被教会定了罪,因之在以后的七年中,加利略停止了发表他在天文学 上的論辯文章。1623年,加利略的朋友,也是素来敬慕他的人,馬费阿·巴伯里宁 (Maffeo Barberini)被选为教皇。加利路盼望着他的天文著作可以得到較好的处 境,于是开始写出他那关于两种不同宇宙覌这一名著,这本书在1632年出版。何 因为这本书肯定地支持了哥白尼理論,結果还是被教会禁止銷售,而且将他停到罗 5六六 (30 甲亚 图12在阿斯提的加利咯别翼中的起居室

对 20 第-一章十七世記中的材科力学 偶受审。在罗馬他被判了罪并逼他改变自已的論点。他回到佛罗侖藤以后,在他 的阿斯提(A心erti,意大利地名)别墅里度完他疑后入年全然隐居的生活,在那段 时期他写出他的名著两种新的科学(TwoN6 w Sciences),书中扼要地陈逃了 以前他在力学中各方面的研究成果。这本书于1638年由莱登(L®iden,荷兰海牙 邻近都市名,释者注)的阿尔齐菲斯(Ez8vs)出版商所出版(图13)。书中一部分 鼓到建筑材料的力学性眉和梁的强度,成为材料力学領城中的第一本著作,从邢时 起,彈性体的力学史也就开了端。 DISCOR SI DIMOSTRAZIONI MATEMATICHE, intarno die nsoue cien之e Attenenti alz MECANICA &i MoVIMENTI LOCAL delsigner GALILEO GALILEI LINCEO, Filofofoe Matematico primario del Sereniffimo Grand Duca di Tofcana. Comvne Appendice deleemtro ligramitidaleumiSolids. IN LEIDA Appe6g效fevitii.v.p.&xvu 田13如利略著:《两种新的利学一书的里封面 2.加利略在材料力学上的责献 加利略在材料力学上所有的貢献都包括在他所著“两种新的科学”一书中的起 先两个对話里。·他以参魂威尼斯一家兵工厂时所作的儿个視察作为开始,井討論 【1]如利降著:“两种渐的释学”由Henry C-啊和A1 fonso d6avio原成英文,在1983年由粗約 Macmilla知公司出反

2。加利略在材料力学上的真款 1打 到一些几何相似的结构物。他說,如果我們使钻构物作成几何相似,則尺寸念是增 大,它們使变得愈为软弱。在說明中,他說道:“一个小型的方失塔、柱子或其他固 体形状,无論平放或者谊立都不会发生断裂的危险,而那些很大的则在稍微蚀动一 下就很容易崩散破碎,这完金是由于它們自已的重量所起的作用”。为了証明这点, 他开始用簡单拉伸的方法来研究材料的强度(图14),說明了一一根杆件的强度是与 它的截面积成正比,而与其长度无关。他称杆子的这种强度为“断裂时的絕对抗 图14加利略的拉伸 就验示意图 图16加利略的弯曲武驗示意图 力”,井且給出了关于铜的极限强度的一些数据,得出了一根杆子的絕对抗力后,他 便进而研究同一杆子用作悬臂梁而在自由端载以荷重使之折断时的抗力(图15)。 他說:“很清楚地,如果杆件断裂,裂口一定发生在B处,該处榫眼边緣充当杠杆 BC的支点,而力就是作用在这里的;杆的厚度BA为杠杆的另一臂,沿BA存在着 抗力。此抗力抵抗着墙外的BD部分与墙内部牙相分离。从以上所逃,可知作用 于C处的力的大小对棱柱杆厚度处的抗力的大小之比(棱柱杆的厚度系指BA 端和其接連部分的嵌接高度),等于BA长度之牛对BC长度之比值。我們可以 看到加利略的假定是:当发生断裂时“抗力”是均匀地分布在截面BA.上的(图16b)。 假設此杆为矩形截面,面且材料在断裂以前一直服从虎克定律,我們得出如图16c [1]Prismatical Bar. 「2:見“两种新的科学英正水.第115直

12 第一章十七世杞中的材料力学 所示的应力分布楷况。相应于此应力分布的抗力偶仅等于加利咯所假被的力矩的 三芬之一。子是对于这种材料,根据加利略的理骼所得出的数值要此C点的实际 断裂栽荷值大三倍。实际材料在破坏 以前井不服从虎克定律,而且在断裂 时的应力芬布地与图16c所示的不 (a) 6) 同,按照这祥的一种說法,就能把加利 图16 略理論所預的和断裂截荷实际数随 之間的差异子以消除了。 两利路根据他的理論得出几条重要的結舱。他对一根矩形梁提出了这样一个 周題:“一根細杆,甚或一粮粗杆,它的宽度較厚度为大,当力作用在宽度方向与作 用在厚度方向相此較时,武問它們对于抵抗断裂的能力究凳何者为大而其比例父 如何?”利用他自己的假股(图16),他作出了正确的答案:“任-一条木尺或粗杆, 如果它的寬度较厚度为大,則依寬边盛立时,:其抵抗断裂的能力要比乎放时为大, 其此例恰为宽度对厚度之比。 加利路进一步剂論了悬臂梁的問題,如截面保持不变,他断定由梁重所产生的 弯矩和长度的不方成正比。如果使圆截面杆的长度不变而改变其牛箜,加利路发 觉抗力矩与半每立方成正比。此一结果符合了“貂对抗力与圓杆藏面积成正比面 抗力偶的背等于圆杆的半徑这一事实。 談到在本身重量作用下的几何相似的悬臂梁,加利路的結論是:固定端的湾矩 增加是和长度的四次方成正比而抗力矩是与接尺度的三次方成正此。这說明了几 何相似的梁其强度井不等同。尺寸愈大,梁就意弱,最后,当梁的尺寸甚大时,它們 E 会只由于其自重作用而破坏。他更观察到要保持强度不变时,截面尺寸的瑜抑率 一定要此长度增加森大些。 有了这些見解以后,加利略写出下面的重要曦論:“你們能清楚地知道,无論是 人工的或天然的結构物,都不可能将尺寸瑜加到弗常大;同样也不可能将船只:、宫 殿或庙字造得非常互大而能使它們的船桨、庭院、梁、铁螺栓以及其他部件都能枯 合在一起;自然界也不能生出异乎寻常的大树,因为桃枝在其本身重量作用下是会 折断的;因此倘若人的、馬的或其他动物的身体高度玲加得异常高,那末这些动物的 骨胳組織就不可能结合在一起来完成其正常机能;因为高度增加只能由較平常的 骨路更硬更强力的质料或者借放大骨路才能达到目的,这样会改变它們的形体,以 至使它們的形肤变成一个互灵怪物…。如果缩小一物体的尺寸,該物体的强度 [1]兒两种新的科学英本,第118質
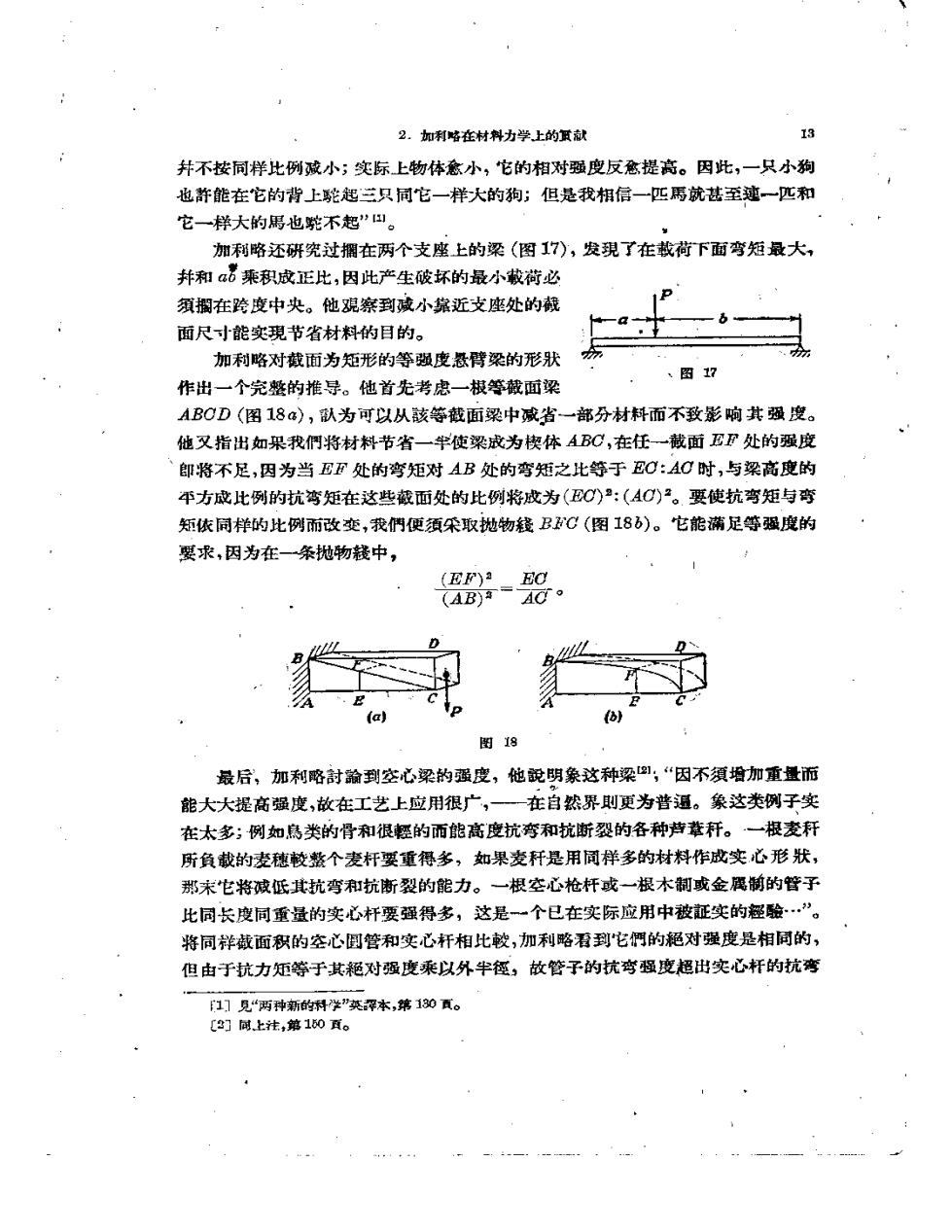
2.如利略在材料力学上的贯献 13 井不按同样比例减小;实际上物体愈小,它的相对强度反愈提高。因此,一只小狗 也許能在它的背上駝起三只同它一样大的狗;但是我相信一一匹馬就甚至建一匹和 它一样大的思也驼不起”田。 加利路还研究过擱在两个支座上的梁(图1T),发現了在載荷下面弯矩最大, 井和a乘积成正比,因此产生破坏的最小较荷必 須攔在跨度中央。他覌察到减小靠近支座处的截 面尺寸能实现节省材料的目的。 加利咯对截面为矩形的等强度数臂梁的形状 图17 作出一个完整的推导。他首先考虑一根等截面梁 AB0D(图18a),队为可以从該等截面梁中减省一部分材料而不致影响其强度。 他又指出如果我們将材料节省一竿使梁成为楔体ABC,在任一截面EF处的强度 即将不足,因为当EF处的弯矩对AB处的弯矩之比等于0:A0时,与梁高度的 平方成比例的抗湾矩在这些截面处的此例将成为(0)2:(AC)。要使抗弯矩与弯 知依同样的比例而改变,我俏便須朵取抛物後BC(图18)。它能满足等强度的 要求,因为在一条抛物钱中, (EF)a EO AB)=AC。 a 图18 最后,加利路討渝到空心梁的强度,他說明象这种梁:“因不須增加重量而 能大大提高强度,故在工艺上应用很广,一一在自然界則更为普通。象这类例子实 在太多;例如焦类的骨和很輕的而能高度抗弯和抗断裂的各种芦巷秆。一根麦秆 所負截的麦穗较整个麦杆要重得多,如果麦秆是用同样多的材料作成实心形状, 那末它将减低其抗弯和抗断裂的能力。一根空心枪杆或一根木制或金属制的管子 比同长度同重量的实心杆要强得多,这是一个已在实际应用中被証实的經驗…”。 将同祥藏面积的空心倒管和实心杆相比較,加利略看到它們的絕对强度是相同的, 但由于抗力矩等子其絕对强度乘以外牛每,故管子的抗弯强度超出实心杆的抗弯 1]見“两种新的村学”英深本,第130瓦。 C3]间.上注,第150页