
例 yc+1)-yx,)_y0x)-y0x,-1) yx,≈ h h h yc,+1)-2yx,)-yc;-) h2 y+1-2y-y:-1 h2 电子科技大学研究生课程 2020.9
电子科技大学研究生课程 2020.9 2 i 1 i i 1 2 i 1 i i 1 i 1 i i i 1 i ' ' h y 2y y h y(x ) 2y(x ) y(x ) h h y(x ) y(x ) h y(x ) y(x ) y (x )

y"(x)-q(x)(x)=f(x) a<x<b y(a)=dl y(b)=d2 微分方程 离散,“差分”近似“微分” yin-2yi-yi=-giy:=fi (i=1,2,3,…n-1) h2 %o =d 代数方程组 yn= d, 节点处的函数值为变量 电子科技大学研究生课程 2020.9
电子科技大学研究生课程 2020.9 y''(x) q(x)y(x) f (x) a x b y(a) d1 y(b) d2 微分方程 2 0 1 2 1 1 ( 1,2,3, 1) 2 y d y d q y f i n h y y y n i i i i i i 代数方程组 离散,“差分”近似“微分” 节点处的函数值为变量
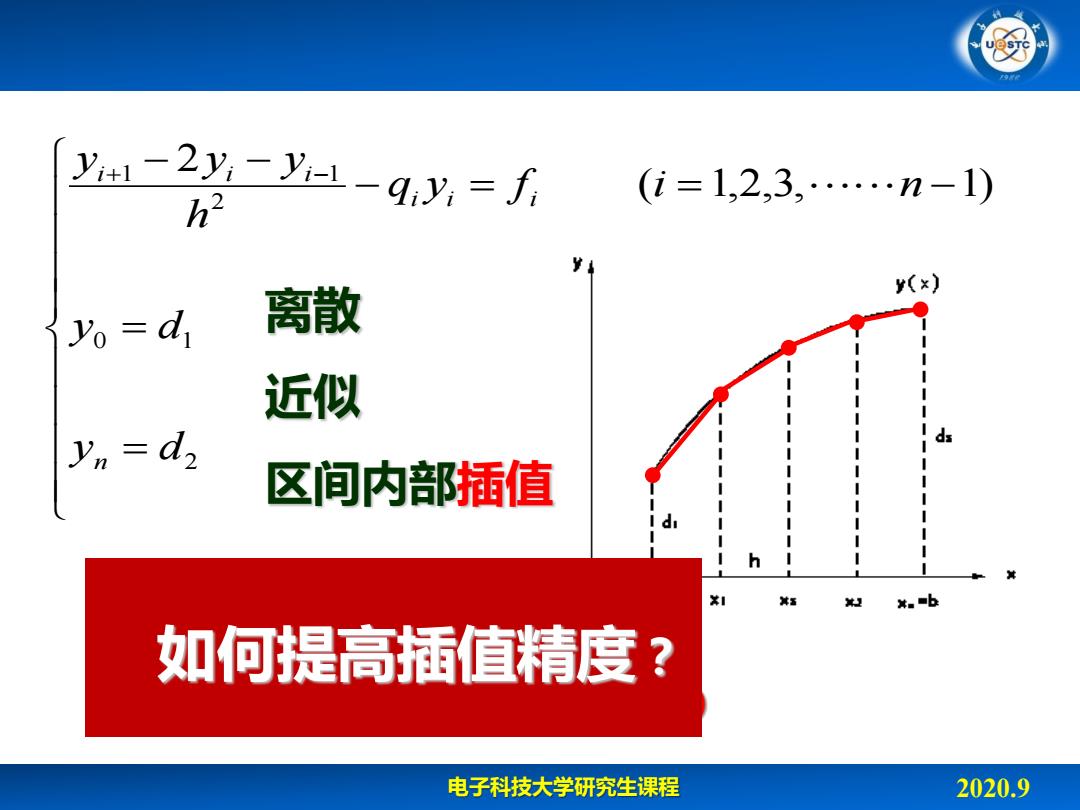
yin-2y-yi=1-qiy,=f (i=1,2,3,…n-1) h2 y(x) yo =d 离散 近似 yn d2 区间内部插值 h 1 其五 以 *。b 如何提高插值精度? 电子科技大学研究生课程 2020.9
电子科技大学研究生课程 2020.9 2 0 1 2 1 1 ( 1,2,3, 1) 2 y d y d q y f i n h y y y n i i i i i i Equations: n+1 Variables: n+1 ( y0 , y1 , y2 , … yn ) 离散 近似 区间内部插值 如何提高插值精度?

二、变分法 Variation method 例 变分原理 微分方程边值问题的解一泛函极值的解 电子科技大学研究生课程 2020.9
电子科技大学研究生课程 2020.9 微分方程边值问题的解 泛函极值的解 二、变分法 Variation method 变分原理

例 d2y +y+1=0 (0,1) dx2 y(0)=0 y(1)=0 -22-2-dx 泛函 电子科技大学研究生课程 2020.9
电子科技大学研究生课程 2020.9 (0) 0 (1) 0 1 0 2 2 y y y d x d y I y x y y y)d x 2 1 2 1 [ ( ) ] ( 2 2 1 0 (0,1) 泛函