
§2 边缘分布 已知联合分布律求边缘分布律 对于二维离散型随机变量(X,Y),己知其联合分布律为 P=PX=x,Y=y,},j=1,2, 喱企雪X的ㄓ炜: 6=bX=x}(小=了.) 6=bk=y-2b区=X·X=}∑ 回鐳”饵「企雪人的ㄓ串沪: 6=bk=}=∑b=x:k=}-∑b 合】返回主目录
已知联合分布律求边缘分布律 对于二维离散型随机变 量(X, Y ),已知其联合分布律为 现求随机变量X的分布律: P = PX = x , Y = y (i,j = 1, 2,) i j i j Pi. = PX = xi ( i =1, 2, ) Pi. = PX = xi = = = j i j P X x , Y y = j ij p §2 边缘分布 P. j = PY = y j = = = i i j P X x , Y y = i ij p 同理,随机变量Y的分布律为: 返回主目录
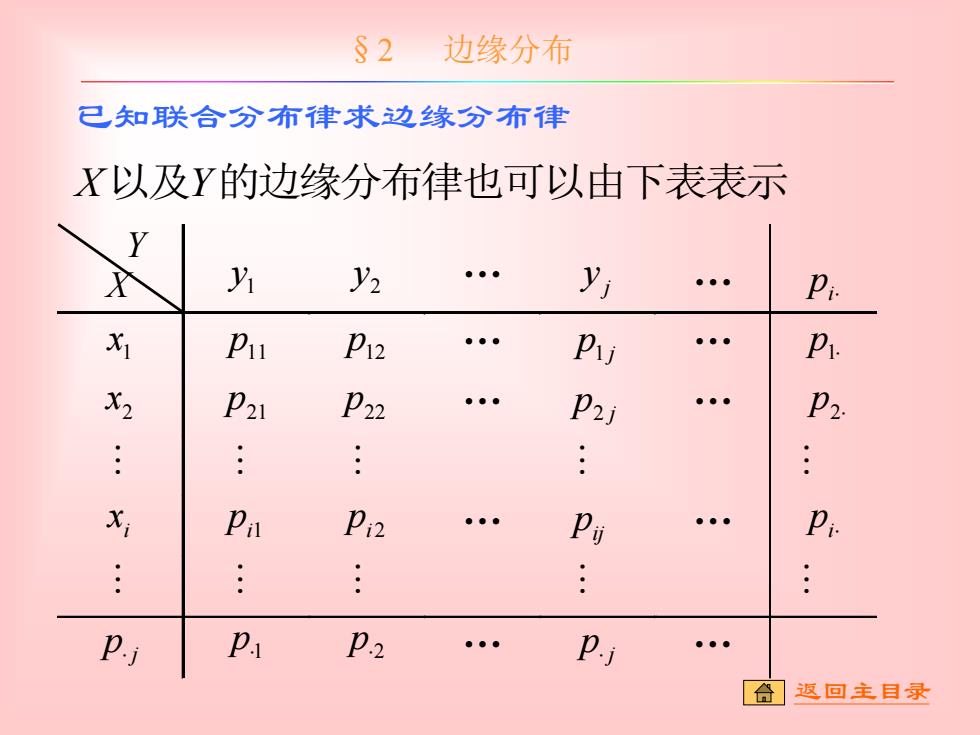
§2边缘分布 已知联合分布律求边缘分布律 X以及Y的边缘分布律也可以由下表表示 y y2 y Pu P12 Pu P X2 P21 P22 p2j P2 Pa Pi2 P可 P P.j p P2 p.j ●●● 合 返回主目录
已知联合分布律求边缘分布律 X以及Y的边缘分布律也可以由下表表示 Y X 1 y 2 y . j y . i p 1 x p11 p12 . j p1 . p1 2 x p21 p22 . p2 j . p2 i x i1 p i2 p . pij . i p p j p1 p2 . p j . §2 边缘分布 返回主目录

§2 边缘分布 例2 出芈库 ¥(人)联号出业炜户X人冬目的师膳 X量YI到X中厘「p赵H一熟赵的熟羽 Y丁丁3寸孚熟中惧「冊一V·业必的熟P 啮X户人的的厚靴昏丁3十坦日人<X 泉<门bX=人=门}=0 泉>4甲好焻 g=”yM汉) 量甲 s=∑浴b=∑b 合】返回主目录
例 2 ( ) 分布律. ,试求 , 的联合分布律与 及 各自的边缘 ,再从 到 中随机地取出一个数, 记所取的数为 从 , 这 个数中随机取出一个, 记所取的数为 Y X Y X Y X 1 X 1 2 3 4 4 解:X 与Y的取值都是 1, 2,3, 4,而且Y X, 所以,当i j时,PX = i,Y = j= 0 §2 边缘分布 当i j时,由乘法公式,得 Pij = PX = i, Y = j = PX = i PY = j X = i i 4i 1 1 4 1 = = 再由 = j i ij p p = i 及 p j pij 返回主目录

§2 边缘分布 例2(续) 山惜(X 人)以人的师谱出典炜羽 X 1 2 3 4 Pi 1 4 0 0 0 + 2 0 0 4 3 2 立 0 4 6 6 石 器 13 7 3 8 合 返回主目录
例 2(续) Y X 1 2 3 4 pi 1 4 1 0 0 0 4 1 2 8 1 8 1 0 0 4 1 3 12 1 12 1 12 1 0 4 1 4 16 1 16 1 16 1 16 1 4 1 p j 48 25 48 13 48 7 48 3 §2 边缘分布 可得(X,Y)与X 及Y的边缘分布律为 返回主目录

§2 边缘分布 例3 炜必尽]冬目的师接出芈炜' 的2中云出中的一最曾新2己二最出熟的联号出ㄓ (⑤)”业回号浮蝉坤悍上出凯斗茛用 赵用一中并押2必·年(I)电兴回号 早20ò0:三最9早50o0Y字实出中避必 一曾并20+·首中一装曾早30ò0:二表曾 啮: 令:X:的甲的2+实曾中的一叢曾熟: 人:赵H2曾中的二最出新 合】返回主目录
例 3 解: 律及它们各自的边缘分布律. 的 件产品中的一等品数与二等品数的联合分布 ⑵.不放回场合这两种情况下,分别计算取出 取出一件,共抽取 次.试在⑴.有放回场合, 占 ,三等品占 .现从这批产品中每次 一批产品共 件,其中一等品占 ,二等品 5 5 50% 20% 50 30% 令:X:取出的5件产品中的一等品数; Y:取出的5件产品中的二等品数. §2 边缘分布 返回主目录