
第四章 随机变量的数字特征 §2方差 §2方差 在实际问题中常关心随机变量与均值的 偏离程度,可用EX-EX,但不方便;所以 通常用E(X-EX)2来度量随机变量X与其均 值EX的偏离程度。 1、定义 设X是随机变量,若E(X-EX)?存在,称其 为随机变量X的方差,记作DX,Var(X,即: DX=VAr(X)=E(X-EX)2。VDX称为标准差 DX=E(X-EXP-∑(-EXP·P’ 离散型。 DX=∫(x-EX)fx, 连续型。 合】返回主目录
§2 方差 1、定义 在实际问题中常关心随机变量与均值的 偏离程度,可用 E|X-EX|,但不方便;所以 通常用 2 E(X − EX ) 来度量随机变量 X 与其均 值 EX 的偏离程度。 设 X 是随机变量,若 2 E(X − EX) 存在,称其 为随机变量 X 的方差,记作 DX,Var(X),即: DX=Var(X)= 2 E(X − EX) 。 DX 称为标准差。 §2 方差 = = − = − 1 2 2 ( ) ( ) i i EX pi DX E X EX x , 离散型。 − DX = (x − EX) f (x)dx 2 , 连续型。 第四章 随机变量的数字特征 返回主目录

第四章 随机变量的数字特征 注:方差描述了随机变量的取值与其 §2方差 均值的偏离程度。 方差也可由下面公式求得: DX=EX,-(EX)为 亚飷 DX=E(X-EX), =E(区,-(6EX)X+(EX)5) =EX,-(6EX)EX+(EX)为 =EX,-5(EX)为+(EX) =EX,-(EX)为 合】返回主目录
§2 方差 第四章 随机变量的数字特征 ( ) 2 2 DX = EX − EX 证明:( ) 2 DX = E X − EX ( ( ) ( ) ) 2 2 = E X − 2EX X + EX ( ) ( ) 2 2 = EX − 2EX EX + EX ( ) ( ) 2 2 2 = EX − 2 EX + EX ( ) 2 2 = EX − EX 方差也可由下面公式求得: 注:方差描述了随机变量的取值与其 均值的偏离程度。 返回主目录
第四章 随机变量的数字特征 §2方差 例13 由’了¥斟平邶]的斟平业本甲上肇总 X:由平中的业激: 人:了平中的业熟 X 8 9 10 P 0.3 0.2 0.5 Y 8 9 10 P 0.2 0.4 0.4 回邮一↓Y的斟平K本女豐5 合】返回主目录
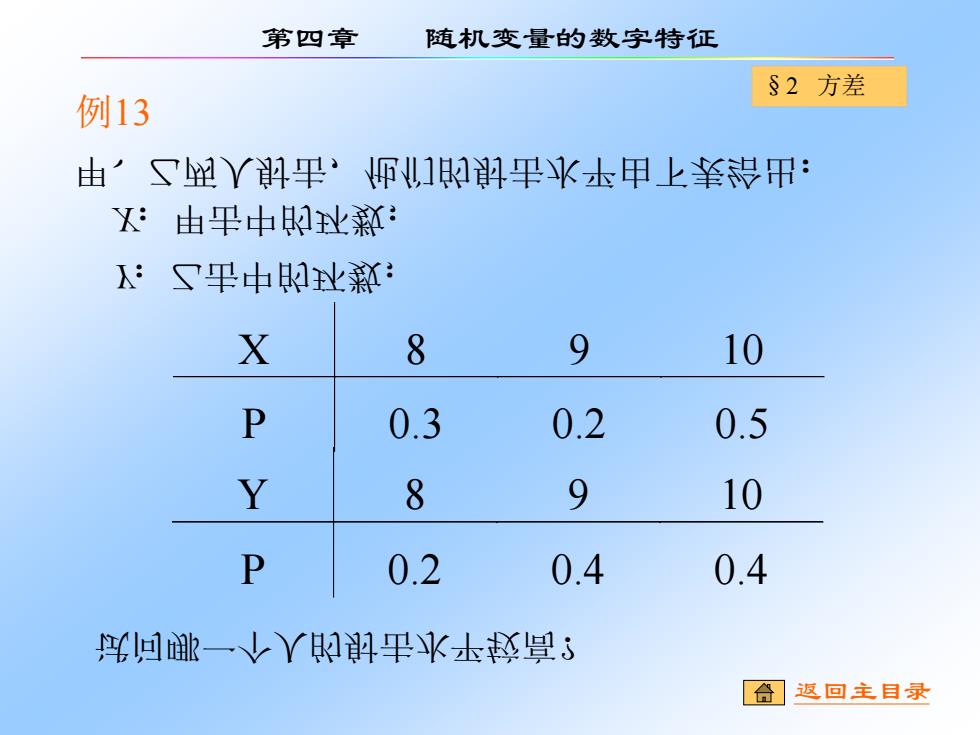
§2 方差 第四章 随机变量的数字特征 甲、乙两人射击,他们的射击水平由下表给出: X:甲击中的环数; Y:乙击中的环数; 试问哪一个人的射击水平较高? 例13 X 8 9 10 P 0.3 0.2 0.5 Y 8 9 10 P 0.2 0.4 0.4 返回主目录

第四章 随机变量的数字特征 §2方差 例13(续) 时: R¥丫的羽业 由的本羽业熟卫 EX=8×03+ò×0下+0×02=∂下 (业) 了的丛羽业熟羽 EX=8×05+ò×0寸+J0×0寸=∂5(业) 的·恒¥V丫平业熟的卫美出沪 屈吓M本问比下皇·由了鲤Y的朗平k本晋一怯 合返回主目录
§2 方差 第四章 随机变量的数字特征 解:比较两个人的平均环数. 甲的平均环数为 EX =80.3+90.2+100.5 = 9.2 (环) 乙的平均环数为 EY =80.2+90.4+100.4 = 9.2 (环) 的,但两个人射击环数的方差分别为 因此,从平均环数上看,甲乙两人的射击水平是一样 例13(续) 返回主目录

第四章 随机变量的数字特征 §2方差 例13(续) DX=(8-∂5),×03+(⊙-ò5)为×0灯+(0-∂5),×02 =0Je Dk=(8-∂5)为×0丁+(6-∂5)为×0寸+(0-∂5)5×0寸 =0Q5寸 甲王D人<DX 区¥的的脾平水本陆罩 合】返回主目录
§2 方差 第四章 随机变量的数字特征 (8 9.2) 0.3 (9 9.2) 0.2 (10 9.2) 0.5 2 2 2 DX = − + − + − = 0.76 (8 9.2) 0.2 (9 9.2) 0.4 (10 9.2) 0.4 2 2 2 DY = − + − + − = 0.624 由于DY DX, 这表明乙的射击水平比甲稳定. 例13(续) 返回主目录