
3.折射 设h>u2 A,C=ACsin i=u,△t AA=ACsin y=u2△i si sm Y U> 入射线、折射线及 折射定律 分界面法线共面 n21:2介质对1介质的相对折射率
3.折射 A A1 A2 B C i u1 u2 A' B' A C ACsin i 2 = = u t 1 AA' = ACsin = u t 2 2 1 2 1 sin sin n u i u = = 入射线、折射线及 分界面法线共面 折射定律 设 u1 u2 n21:2介质对1介质的相对折射率

§16-6 波的干涉 一波的传播规律 口独立性:几列波在媒质中相遇时 各个波将保持本身特性(频率、波长 振动方向等)沿原方向继续传播,与 未相遇一样 叠加原理:在几列波相遇区域,任 一质点的振动为各个波单独在该点 引起的振动的合成
一 .波的传播规律 独立性:几列波在媒质中相遇时, 各个波将保持本身特性(频率、波长、 振动方向等)沿原方向继续传播,与 未相遇一样 叠加原理:在几列波相遇区域,任 一质点的振动为各个波单独在该点 引起的振动的合成 §16-6 波的干涉

二波的干涉 干涉现象:波在媒质 中叠加时,出现某些 地方振动始终加强 某些地方振动始终减 弱或完全抵消的现象 相干波的条件:频率相同, 振动方 向相同,相位相同或相位差恒定
二.波的干涉 干涉现象:波在媒质 中叠加时,出现某些 地方振动始终加强, 某些地方振动始终减 弱或完全抵消的现象 相干波的条件:频率相同,振动方 向相同,相位相同或相位差恒定
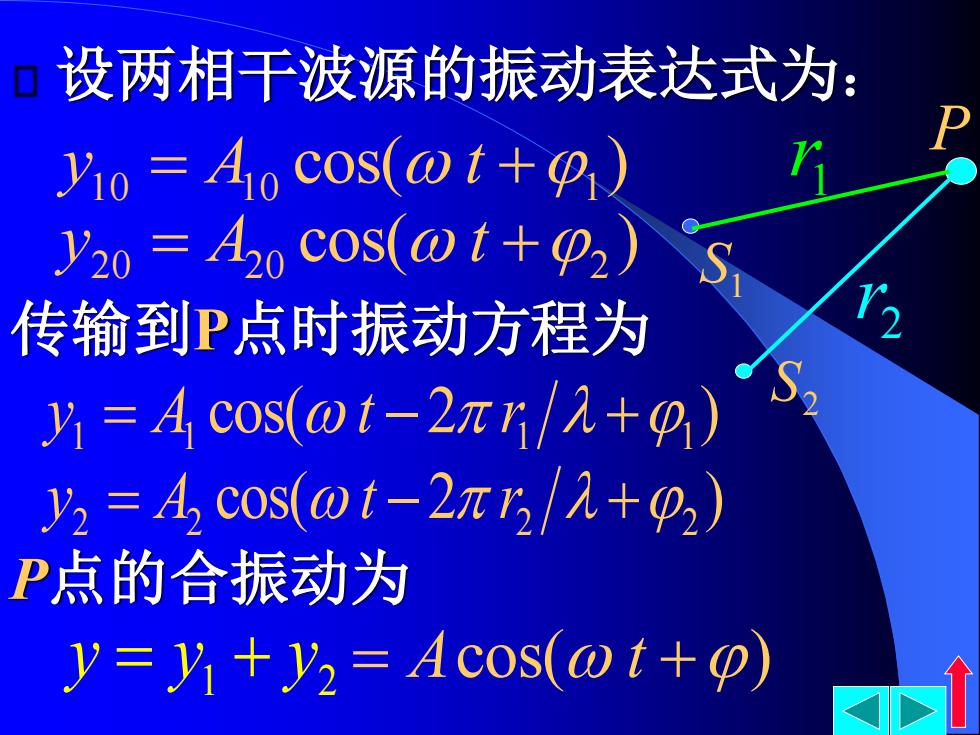
设两相干波源的振动表达式为: Yio Ao cos(@t+) y20=A2oC0s(0t+p2) 传输到P点时振动方程为 片=Acos(wt-2πr/见+0) y2=Ac0s(0t-2π32/见+92) P点的合振动为 y=y+y2=Acos(@t+p)
设两相干波源的振动表达式为: cos( ) 10 = 10 +1 y A t cos( ) 2 0 = 2 0 +2 y A t S1 S2 P 1 r 2 r 传输到P点时振动方程为 cos( 2 ) 1 = 1 − 1 +1 y A t r cos( 2 ) 2 = 2 − 2 +2 y A t r P点的合振动为 1 2 y = y + y = Acos( t +)

其中4术+龙+24w,-8-2) A sin( 22 tgp 22 讨论: 4.coo 空间某点 A0=2,-0,-2元21-恒定 即空间每点有恒定的合振幅A
其中 2 cos( 2 ) 2 1 1 2 2 1 2 2 2 1 r r A A A A A − = + + − − ) 2 ) cos( 2 cos( ) 2 ) sin( 2 sin( 2 2 2 1 1 1 2 2 2 1 1 1 r A r A r A r A t g − + − − + − = 讨论: 空间某点 2 1 2 1 2 r − r = − − 即空间每点有恒定的合振幅A -恒定