
设计要求 设H表示一个散列函数,厂是输入长度的上界,y是比厂小 得多的固定的输出长度 ·单向性:计算一个给定消息串的数字指纹是容易的,但是 找到一个数字指纹对应的消息是困难的 ●对于任意的二进制串x,其中≤「,计算H(X)是容易的, 但是对于一个给定的散列值h(h=W,很难找到它对应 的原像x使得h=H(X) 《计算机网络安全的理论与实践(第2版)》·【美】王杰,高等教育出版社,2011年. 6
6 设计要求 设H 表示一个散列函数, Γ 是输入长度的上界, γ 是比Γ小 得多的固定的输出长度 单向性: 计算一个给定消息串的数字指纹是容易的, 但是 找到一个数字指纹对应的消息是困难的 对于任意的二进制串x ,其中 |x| ≤ Γ, 计算 H(x)是容易的, 但是对于一个给定的散列值h ( |h| = γ), 很难找到它对应 的原像x使得h = H(x) 《计算机网络安全的理论与实践(第2版)》. 【美】王杰, 高等教育出版社, 2011年

设计要求 。计算唯一性:找到两个不同的消息具有相同的数字指纹 是困难的 无碰撞性-给定一个消息X,满足≤厂,找到另一个不同的消 息y(y八≤刀与x具有相同的散列值,即H(X)=Hy),是困难的 ● 强无碰撞性-很难找到两个消息x和y具有相同的散列,即H(X)= H(y) ·注意:不满足强无碰撞性,并不意味着不满足无碰撞性 《计算机网络安全的理论与实践(第2版)》·【美】王杰,高等教育出版社,2011年. 7
7 计算唯一性: 找到两个不同的消息具有相同的数字指纹 是困难的 无碰撞性– 给定一个消息 x,满足|x| ≤ Γ, 找到另一个不同的消 息y (|y| ≤ Γ)与x具有相同的散列值,即H(x) = H(y),是困难的 强无碰撞性– 很难找到两个消息x和y具有相同的散列,即H(x) = H(y) 注意:不满足强无碰撞性,并不意味着不满足无碰撞性 设计要求 《计算机网络安全的理论与实践(第2版)》. 【美】王杰, 高等教育出版社, 2011年

密码散列函数的探索 寻求密码散列函数 尚未知是否存在单向的、计算唯一的密码散列函数 几个曾经被认为是安全的密码散列函数,已被证明不能满足强无碰 撞性 口另一个常用的散列函数SHA-1算法,已经被证明其安全性低于预期 口本节介绍两个标准的密码散列函数SHA-512和VHIRLPOOL 《计算机网络安全的理论与实践(第2版)》:【美】王杰,高等教育出版社,2011年. 8
8 密码散列函数的探索 寻求密码散列函数 尚未知是否存在单向的、计算唯一的密码散列函数 几个曾经被认为是安全的密码散列函数, 已被证明不能满足强无碰 撞性 另一个常用的散列函数SHA-1算法,已经被证明其安全性低于预期 本节介绍两个标准的密码散列函数SHA-512和WHIRLPOOL 《计算机网络安全的理论与实践(第2版)》. 【美】王杰, 高等教育出版社, 2011年
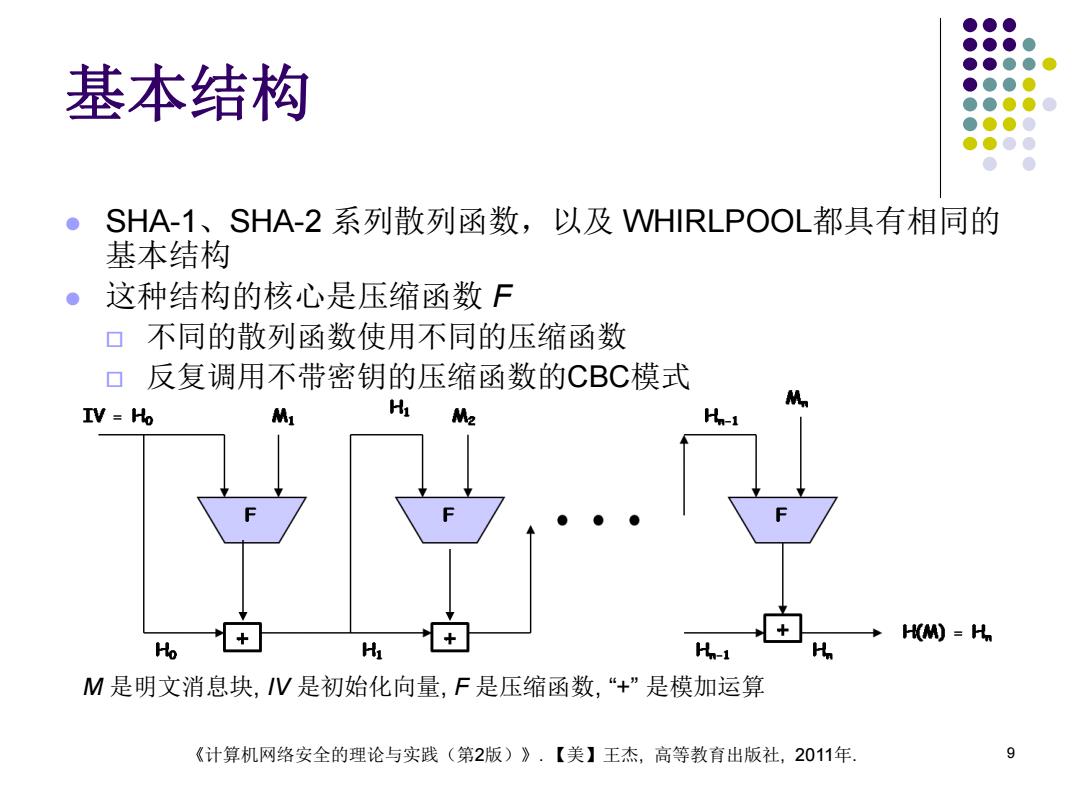
基本结构 ● SHA-1、SHA-2系列散列函数,以及VHIRLPOOL都具有相同的 基本结构 。这种结构的核心是压缩函数F 口不同的散列函数使用不同的压缩函数 口反复调用不带密钥的压缩函数的CBC模式 IV Ho M H 2 H(M)=H Ho H H-1 M是明文消息块,V是初始化向量,F是压缩函数,“+”是模加运算 《计算机网络安全的理论与实践(第2版)》·【美】王杰,高等教育出版社,2011年. 9
9 基本结构 SHA-1、SHA-2 系列散列函数,以及 WHIRLPOOL都具有相同的 基本结构 这种结构的核心是压缩函数 F 不同的散列函数使用不同的压缩函数 反复调用不带密钥的压缩函数的CBC模式 M 是明文消息块, IV 是初始化向量, F 是压缩函数, “+” 是模加运算 《计算机网络安全的理论与实践(第2版)》. 【美】王杰, 高等教育出版社, 2011年
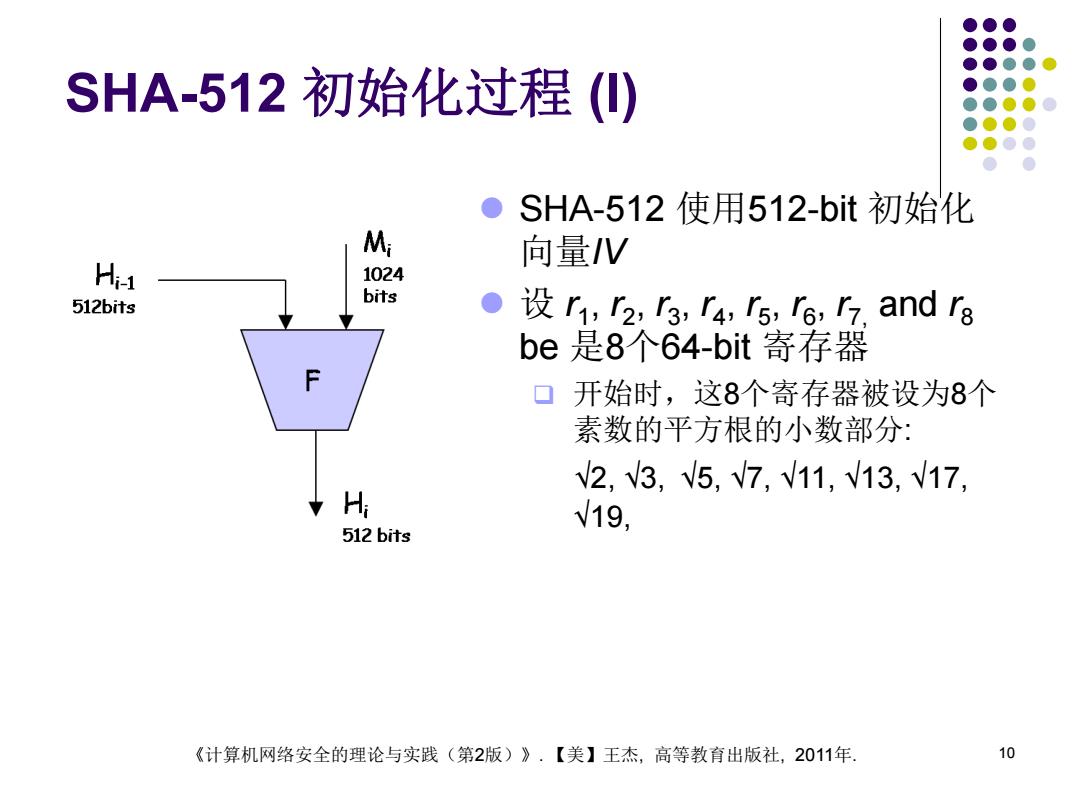
SHA-512初始化过程(0) ● SHA-512使用512-bit初始化 M 向量V Hia 1024 512bits bits ● r2,r3,r rs,e 7 and ra be是8个64-bit寄存器 口开始时,这8个寄存器被设为8个 素数的平方根的小数部分: V2,V3,5,√7,√11,√13,√17, H 19, 512 bits 《计算机网络安全的理论与实践(第2版)》·【美】王杰,高等教育出版社,2011年. 10
10 SHA-512 初始化过程 (I) SHA-512 使用512-bit 初始化 向量IV 设 r1 , r2 , r3 , r4 , r5 , r6 , r7, and r8 be 是8个64-bit 寄存器 开始时,这8个寄存器被设为8个 素数的平方根的小数部分: √2, √3, √5, √7, √11, √13, √17, √19, 《计算机网络安全的理论与实践(第2版)》. 【美】王杰, 高等教育出版社, 2011年