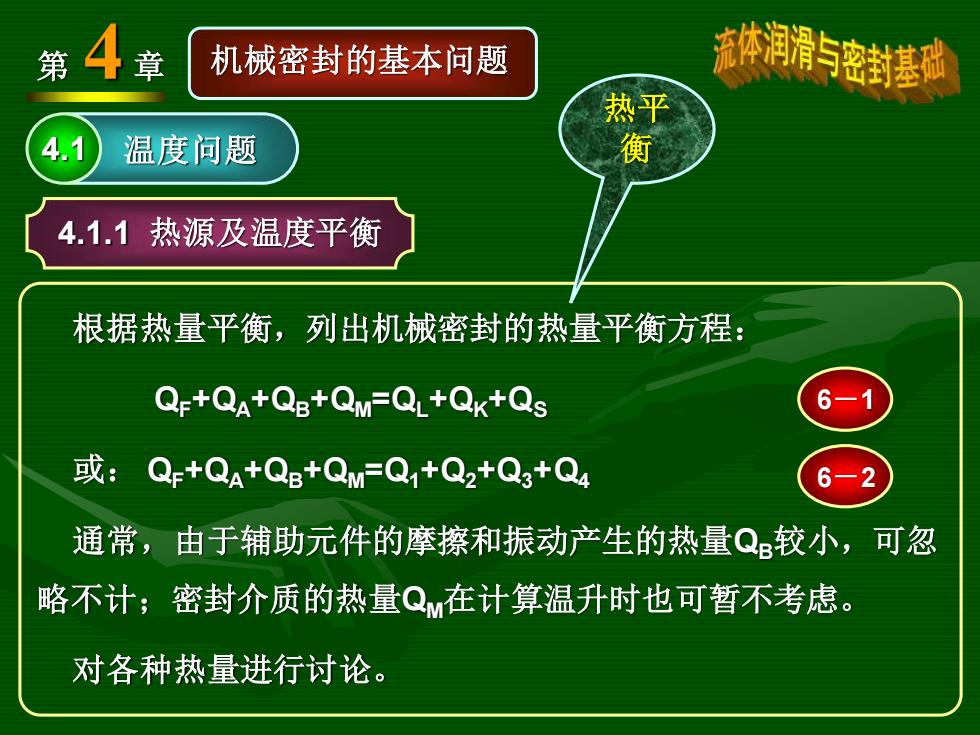
第4章 机械密封的基本问题 流体润滑片密封基础 热平 4.1 温度问题 4.1.1热源及温度平衡 根据热量平衡,列出机械密封的热量平衡方程: QF+QA+Qg+QM=QL+Qk+Qs 6-1 或:Q+Qa+QB+QM=Q1+Q2+Q3+Q4 6-2 通常,由于辅助元件的摩擦和振动产生的热量QB较小,可忽 略不计;密封介质的热量Q在计算温升时也可暂不考虑。 对各种热量进行讨论
第 4 章 机械密封的基本问题 4.1 温度问题 根据热量平衡,列出机械密封的热量平衡方程: QF+QA+QB+QM=QL+QK+QS 或: QF+QA+QB+QM=Q1+Q2+Q3+Q4 通常,由于辅助元件的摩擦和振动产生的热量QB较小,可忽 略不计;密封介质的热量QM在计算温升时也可暂不考虑。 对各种热量进行讨论。 4.1.1 热源及温度平衡 6-1 6-2 热平 衡
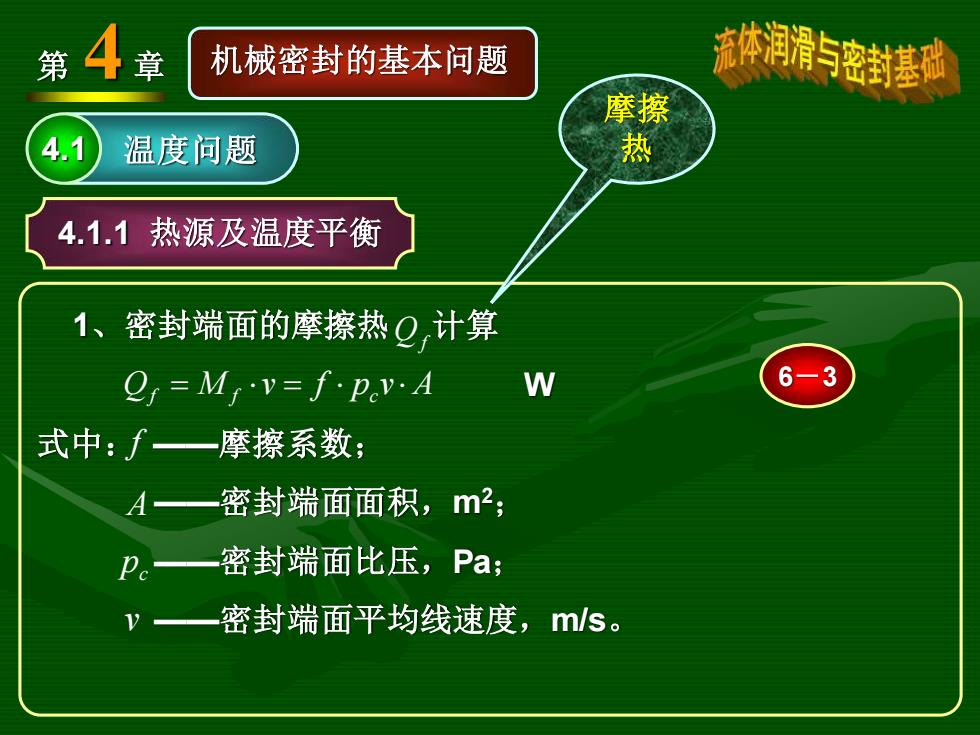
第4章 机械密封的基本问题 流体润滑与密封基地 摩擦 4.1 温度问题 4.1.1热源及温度平衡 1、 密封端面的摩擦热Q,计算 Q=Mrv=f·pvA W 6-3 式中:f一摩擦系数; A一密封端面面积,m2; p。一密封端面比压,Pa 密封端面平均线速度,ms
第 4 章 机械密封的基本问题 4.1 温度问题 4.1.1 热源及温度平衡 1、密封端面的摩擦热 计算 W 式中: ——摩擦系数; ——密封端面面积,m2; ——密封端面比压,Pa; ——密封端面平均线速度,m/s。 Qf = M f v = f pc v A f A c p v Qf 6-3 摩擦 热
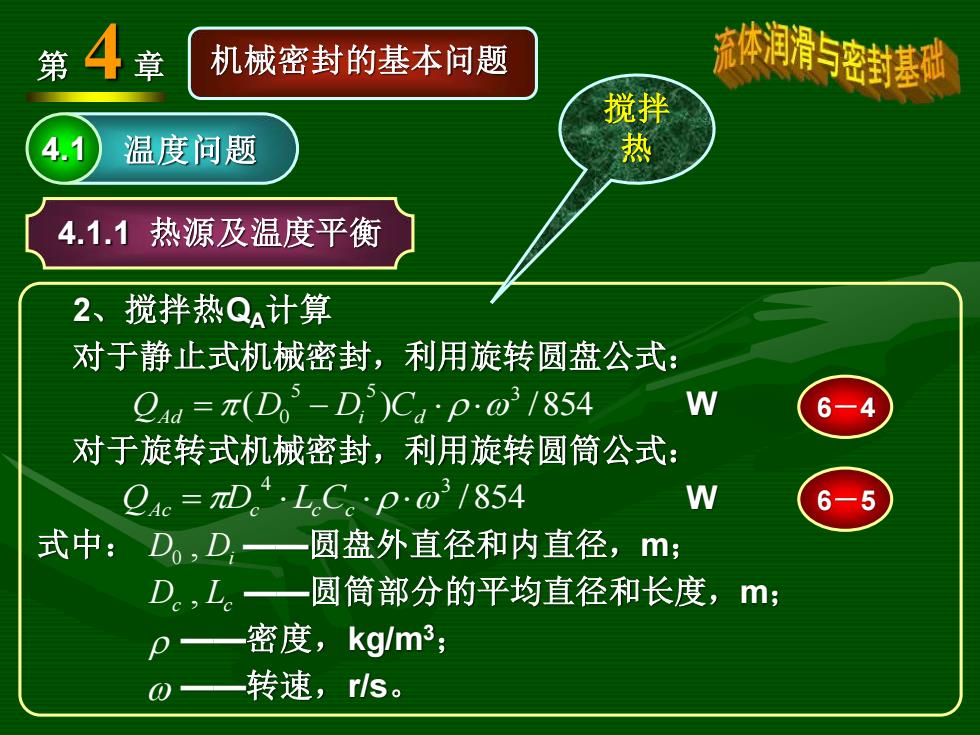
第4 章 机械密封的基本问题 流体润滑与密封基砂 搅拌 4.1 温度问题 热 4.1.1热源及温度平衡 2、搅拌热Q计算 对于静止式机械密封,利用旋转圆盘公式: 2ad (Do-D)Cap:@1854 W 6-4 对于旋转式机械密封,利用旋转圆筒公式: Qc=πD。.L.C。·po3/854 W 6-5 式中:Do,D一圆盘外直径和内直径,m; D。,L。一圆筒部分的平均直径和长度,m; 密度,kglm3; o一转速,rls
第 4 章 机械密封的基本问题 4.1 温度问题 4.1.1 热源及温度平衡 2、搅拌热QA计算 对于静止式机械密封,利用旋转圆盘公式: W 对于旋转式机械密封,利用旋转圆筒公式: W 式中: ——圆盘外直径和内直径,m; ——圆筒部分的平均直径和长度,m; ——密度,kg/m3; ——转速,r/s。 ( ) /854 5 5 3 QAd = D0 − Di Cd D Di , 0 6-4 /854 4 3 QAc =Dc Lc Cc 6-5 Dc Lc , 搅拌 热
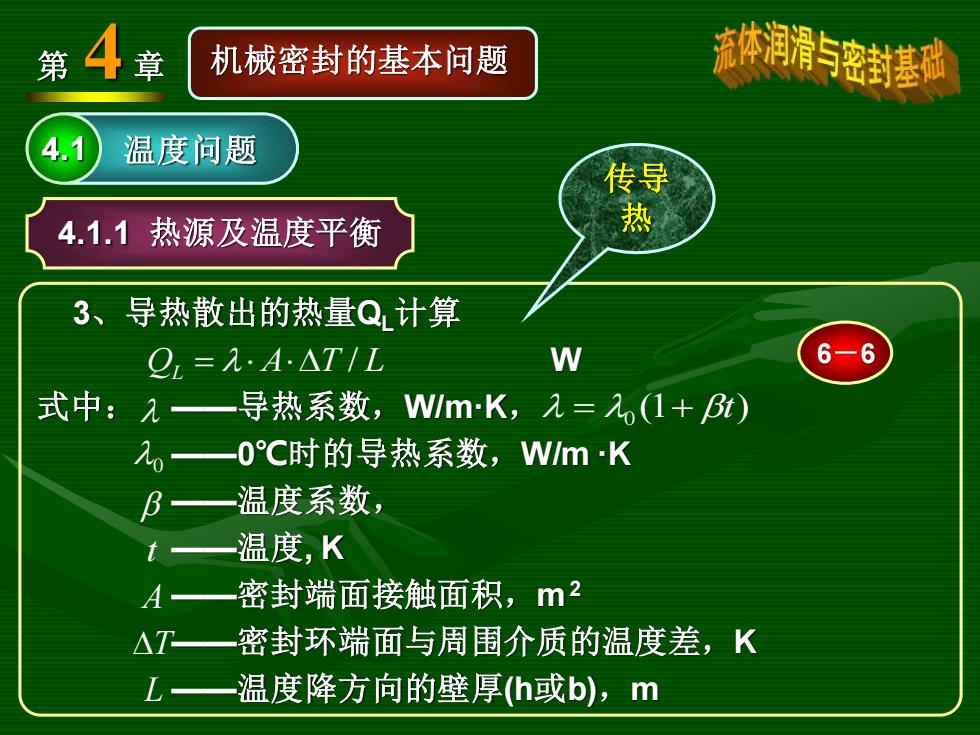
第4章 机械密封的基本问题 流体润滑5密封基础 4.1 温度问题 传导 4.1.1热源及温度平衡 3、导热散出的热量Q计算 9=九·A△T/L W 6-6 式中:2一导热系数,WlmK,入=,(1+B) 一0C时的导热系数,WmK B一温度系数, t 温度,K A 密封端面接触面积,m2 △T—密封环端面与周围介质的温度差,K L一温度降方向的壁厚(h或b),m
第 4 章 机械密封的基本问题 4.1 温度问题 4.1.1 热源及温度平衡 3、导热散出的热量QL计算 W 式中: ——导热系数,W/m·K, ——0℃时的导热系数,W/m ·K ——温度系数, ——温度, K ——密封端面接触面积,m2 ——密封环端面与周围介质的温度差,K ——温度降方向的壁厚(h或b),m QL = AT / L T 6-6 A 0 (1 ) 0 = + t t L 传导 热
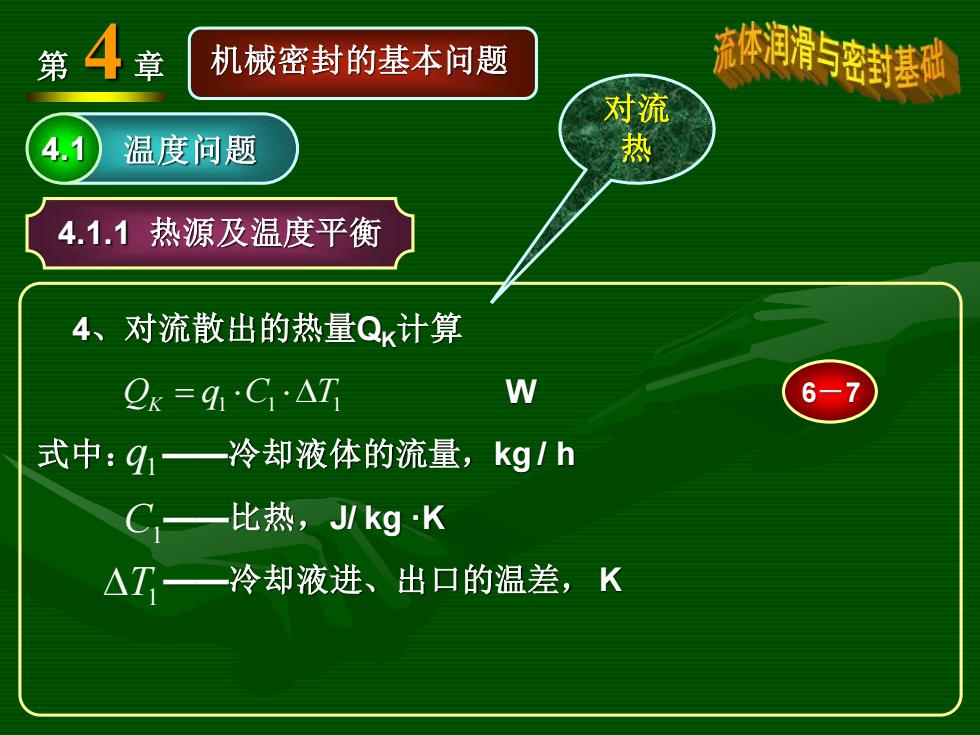
第4 章 机械密封的基本问题 流体润滑与密封基砂 对流 4.1 温度问题 热 4.1.1热源及温度平衡 4、对流散出的热量Qk计算 Qx=4C·△T W 6-7 式中:q1一冷却液体的流量,kg/h C一比热,J/kgK △T一冷却液进、出口的温差,K
第 4 章 机械密封的基本问题 4.1 温度问题 4.1.1 热源及温度平衡 4、对流散出的热量QK计算 W 式中: ——冷却液体的流量,kg / h ——比热,J/ kg ·K ——冷却液进、出口的温差, K QK q1 C1 T1 = q1 6-7 C1 T1 对流 热