安徽理工大学：《智能控制及仿真》课程教学资源（课件讲义）第5章 自适应模糊控制

5.1.3仿真实例 实例1针对一维函数g,设计一个模糊系统)，使 之一致的逼近定义在v=-3上的连续函数g(x)=sin(x), 所需精度为ε=0.2，即spls()-f(x川<6

5.1.3 仿真实例 实例1 针对一维函数 ，设计一个模糊系统 ，使 之一致的逼近定义在 上的连续函数 ， 所需精度为 ，即 。 gx f x U  3, 3 gx  sinx   0.2         g x f x x U sup

由于 =lcos(x儿。=1，由式(5.3)可 知1 h=h,故取h≤02满足精度要求。取h=0.2, 则模糊集的个数为N=2+1=31。在U=3,3上定义31个具有 三角形隶属函数的模糊集4，如图5-1所示。所设计的 模糊系统为： .分m6h 三(

由 于 ， 由 式 （ 5 . 3 ） 可 知， ，故取 满足精度要求。取 ， 则模糊集的个数为 。在 上定义31个具有 三角形隶属函数的模糊集 ，如图5-1所示。所设计的 模糊系统为：  cos    1     x x g h h x g g f        h  0.2 h  0.2  1  31 h L N U   3,3 j A              31 1 31 1 sin j j A j j A j x e x f x  

1 0.8 0.6 0.4 0.2 -3 -2 0 3 X 图5-1 隶属函数

- 3 - 2 - 1 0 1 2 3 0 0 . 2 0 . 4 0 . 6 0 . 81 x Membership function 图5-1 隶属函数

维函数逼近仿真程序见chap51.m。逼近效果如 图5-2和5-3所示： 0.5 0.5 -3 -2 -1 0 7 图5-2模糊逼近

一维函数逼近仿真程序见chap5_1.m。逼近效果如 图5-2和5-3所示： -3 -2 -1 0 1 2 3 -1 -0.5 0 0.5 1 x A p pro a c hin g 图5-2 模糊逼近

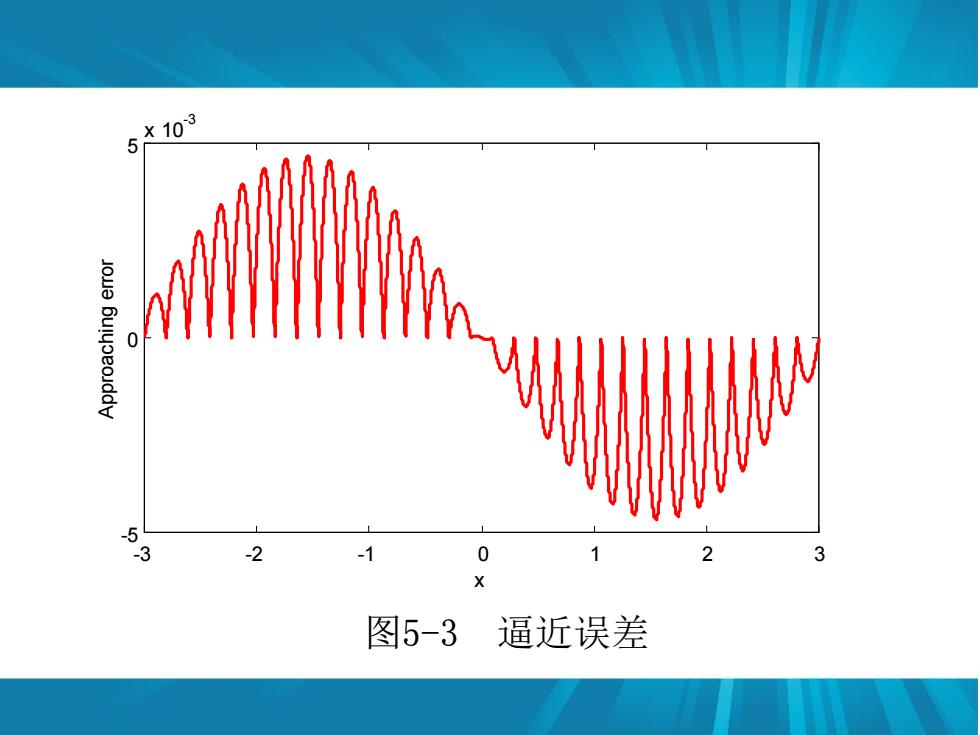
5103 0 -5 -3 -2 -1 0 2 3 图5-3 逼近误差

-3 -2 -1 0 1 2 3 -5 0 5 x 10 -3 x A p pro a c hin g error 图5-3 逼近误差