【智能系统】应用iki-means算法实现标记分布学习

第12卷第3期 智能系统学报 Vol.12 No.3 2017年6月 CAAI Transactions on Intelligent Systems Jun.2017 D0I:10.11992/is.201704024 网络出版地址：http:/kns.cmki.net/kcms/detail/23.1538.TP.20170704.0925.002.html 应用k-means算法实现标记分布学习 邵东恒，杨文元，赵红 (闯南师范大学粒计算重点实验室，福建漳州363000) 摘要：标记分布学习是近年来提出的一种新的机器学习范式，它能很好地解决某些标记多义性的问题。现有的标 记分布学习算法均利用条件概率建立参数模型，但未能充分利用特征和标记间的联系。本文考虑到特征相似的样 本所对应的标记分布也应当相似，利用原型聚类的k均值算法(k-meas),将训练集的样本进行聚类，提出基于 means算法的标记分布学习(label distribution learning based on-means algorithm,LDLKM)。首先通过聚类算法k: meas求得每一个簇的均值向量，然后分别求得对应标记分布的均值向量。最后将测试集和训练集的均值向量间的 距离作为权重，应用到对测试集标记分布的预测上。在6个公开的数据集上进行实验，并与3种已有的标记分布学 习算法在5种评价指标上进行比较，实验结果表明提出的LDLKM算法是有效的。 关键词：标记分布：聚类：k-means;闵可夫斯基距离；多标记：权重矩阵；均值向量；softmax函数 中图分类号：TP181文献标志码：A文章编号：1673-4785(2017)03-0325-08 中文引用格式：邵东恒，杨文元，赵红.应用k-meas算法实现标记分布学习[J].智能系统学报，2017,12(3)：325-332 英文引用格式：SHAO Dongheng,YANG Wenyuan,ZHAO Hong.Label distribution learning based on k-means algorithm[J]. CAAI transactions on intelligent systems,2017,12(3):325-332. Label distribution learning based on k-means algorithm SHAO Dongheng,YANG Wenyuan,ZHAO Hong (1.Lab of Granular Computing,Minnan Normal University,Zhangzhou 363000,China) Abstract:Label distribution learning is a new type of machine learning paradigm that has emerged in recent years. It can solve the problem wherein different relevant labels have different importance.Existing label distribution learning algorithms adopt the parameter model with conditional probability,but they do not adequately exploit the relation between features and labels.In this study,the k-means clustering algorithm,a type of prototype-based clustering,was used to cluster the training set instance since samples having similar features have similar label distribution.Hence,a new algorithm known as label distribution learning based on k-means algorithm (LDLKM) was proposed.It firstly calculated each cluster's mean vector using the k-means algorithm.Then,it got the mean vector of the label distribution corresponding to the training set.Finally,the distance between the mean vectors of the test set and the training set was applied to predict label distribution of the test set as a weight.Experiments were conducted on six public data sets and then compared with three existing label distribution learning algorithms for five types of evaluation measures.The experimental results demonstrate the effectiveness of the proposed KM-LDL algorithm Keywords:label distribution;clustering;k-means;Minkowski distance;multi-label;weight matrix;mean vector; softmax function 近年来，标记多义性问题是机器学习和数据挖 记的多标记学习(muli-label learning)[。多标记学 掘领域的热门问题。目前已有的两种比较成熟的 习是对单标记学习的拓展[)。通常多标记学习能 学习范式是对每个实例分配单个标记的单标记学 处理一个实例属于多个标记的分歧情况。通过大 习(single-label learning)和对一个实例分配多个标 量的研究和实验3表明，多标记学习是一种有效 且应用范围较广的学习范式。 收稿日期：2017-04-19.网络出版日期：2017-07-04. 基金项目：国家自然科学基金项目(61379049,61379089) 多标记学习虽然对于一个实例允许标上多个 通信作者：杨文元.E-mail:yang叮y@xmu.cdu.cm

第 １２ 卷第 ３ 期 智 能 系 统 学 报 Ｖｏｌ．１２ №．３ ２０１７ 年 ６ 月 ＣＡＡＩ Ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ Ｉｎｔｅｌｌｉｇｅｎｔ Ｓｙｓｔｅｍｓ Ｊｕｎ． ２０１７ ＤＯＩ：１０．１１９９２ ／ ｔｉｓ．２０１７０４０２４ 网络出版地址：ｈｔｔｐ： ／ ／ ｋｎｓ．ｃｎｋｉ．ｎｅｔ ／ ｋｃｍｓ／ ｄｅｔａｉｌ ／ ２３．１５３８．ＴＰ．２０１７０７０４．０９２５．００２．ｈｔｍｌ 应用 ｋ⁃ｍｅａｎｓ 算法实现标记分布学习 邵东恒，杨文元，赵红 （闽南师范大学 粒计算重点实验室，福建 漳州 ３６３０００） 摘 要：标记分布学习是近年来提出的一种新的机器学习范式，它能很好地解决某些标记多义性的问题。 现有的标 记分布学习算法均利用条件概率建立参数模型，但未能充分利用特征和标记间的联系。 本文考虑到特征相似的样 本所对应的标记分布也应当相似，利用原型聚类的 ｋ 均值算法（ ｋ⁃ｍｅａｎｓ），将训练集的样本进行聚类，提出基于 ｋ⁃ ｍｅａｎｓ 算法的标记分布学习（ ｌａｂｅｌ ｄｉｓｔｒｉｂｕｔｉｏｎ ｌｅａｒｎｉｎｇ ｂａｓｅｄ ｏｎ ｋ⁃ｍｅａｎｓ ａｌｇｏｒｉｔｈｍ，ＬＤＬＫＭ）。 首先通过聚类算法 ｋ⁃ ｍｅａｎｓ 求得每一个簇的均值向量，然后分别求得对应标记分布的均值向量。 最后将测试集和训练集的均值向量间的 距离作为权重，应用到对测试集标记分布的预测上。 在 ６ 个公开的数据集上进行实验，并与 ３ 种已有的标记分布学 习算法在 ５ 种评价指标上进行比较，实验结果表明提出的 ＬＤＬＫＭ 算法是有效的。 关键词：标记分布；聚类；ｋ－ｍｅａｎｓ；闵可夫斯基距离；多标记；权重矩阵；均值向量；ｓｏｆｔｍａｘ 函数 中图分类号：ＴＰ１８１ 文献标志码：Ａ 文章编号：１６７３－４７８５（２０１７）０３－０３２５－０８ 中文引用格式：邵东恒，杨文元，赵红．应用 ｋ⁃ｍｅａｎｓ 算法实现标记分布学习［Ｊ］． 智能系统学报， ２０１７， １２（３）： ３２５－３３２． 英文引用格式：ＳＨＡＯ Ｄｏｎｇｈｅｎｇ， ＹＡＮＧ Ｗｅｎｙｕａｎ， ＺＨＡＯ Ｈｏｎｇ． Ｌａｂｅｌ ｄｉｓｔｒｉｂｕｔｉｏｎ ｌｅａｒｎｉｎｇ ｂａｓｅｄ ｏｎ ｋ⁃ｍｅａｎｓ ａｌｇｏｒｉｔｈｍ［ Ｊ］． ＣＡＡＩ ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ ｉｎｔｅｌｌｉｇｅｎｔ ｓｙｓｔｅｍｓ， ２０１７， １２（３）： ３２５－３３２． Ｌａｂｅｌ ｄｉｓｔｒｉｂｕｔｉｏｎ ｌｅａｒｎｉｎｇ ｂａｓｅｄ ｏｎ ｋ⁃ｍｅａｎｓ ａｌｇｏｒｉｔｈｍ ＳＨＡＯ Ｄｏｎｇｈｅｎｇ， ＹＡＮＧ Ｗｅｎｙｕａｎ， ＺＨＡＯ Ｈｏｎｇ （１． Ｌａｂ ｏｆ Ｇｒａｎｕｌａｒ Ｃｏｍｐｕｔｉｎｇ， Ｍｉｎｎａｎ Ｎｏｒｍａｌ Ｕｎｉｖｅｒｓｉｔｙ， Ｚｈａｎｇｚｈｏｕ ３６３０００， Ｃｈｉｎａ） Ａｂｓｔｒａｃｔ：Ｌａｂｅｌ ｄｉｓｔｒｉｂｕｔｉｏｎ ｌｅａｒｎｉｎｇ ｉｓ ａ ｎｅｗ ｔｙｐｅ ｏｆ ｍａｃｈｉｎｅ ｌｅａｒｎｉｎｇ ｐａｒａｄｉｇｍ ｔｈａｔ ｈａｓ ｅｍｅｒｇｅｄ ｉｎ ｒｅｃｅｎｔ ｙｅａｒｓ． Ｉｔ ｃａｎ ｓｏｌｖｅ ｔｈｅ ｐｒｏｂｌｅｍ ｗｈｅｒｅｉｎ ｄｉｆｆｅｒｅｎｔ ｒｅｌｅｖａｎｔ ｌａｂｅｌｓ ｈａｖｅ ｄｉｆｆｅｒｅｎｔ ｉｍｐｏｒｔａｎｃｅ． Ｅｘｉｓｔｉｎｇ ｌａｂｅｌ ｄｉｓｔｒｉｂｕｔｉｏｎ ｌｅａｒｎｉｎｇ ａｌｇｏｒｉｔｈｍｓ ａｄｏｐｔ ｔｈｅ ｐａｒａｍｅｔｅｒ ｍｏｄｅｌ ｗｉｔｈ ｃｏｎｄｉｔｉｏｎａｌ ｐｒｏｂａｂｉｌｉｔｙ， ｂｕｔ ｔｈｅｙ ｄｏ ｎｏｔ ａｄｅｑｕａｔｅｌｙ ｅｘｐｌｏｉｔ ｔｈｅ ｒｅｌａｔｉｏｎ ｂｅｔｗｅｅｎ ｆｅａｔｕｒｅｓ ａｎｄ ｌａｂｅｌｓ． Ｉｎ ｔｈｉｓ ｓｔｕｄｙ， ｔｈｅ ｋ⁃ｍｅａｎｓ ｃｌｕｓｔｅｒｉｎｇ ａｌｇｏｒｉｔｈｍ， ａ ｔｙｐｅ ｏｆ ｐｒｏｔｏｔｙｐｅ⁃ｂａｓｅｄ ｃｌｕｓｔｅｒｉｎｇ， ｗａｓ ｕｓｅｄ ｔｏ ｃｌｕｓｔｅｒ ｔｈｅ ｔｒａｉｎｉｎｇ ｓｅｔ ｉｎｓｔａｎｃｅ ｓｉｎｃｅ ｓａｍｐｌｅｓ ｈａｖｉｎｇ ｓｉｍｉｌａｒ ｆｅａｔｕｒｅｓ ｈａｖｅ ｓｉｍｉｌａｒ ｌａｂｅｌ ｄｉｓｔｒｉｂｕｔｉｏｎ． Ｈｅｎｃｅ， ａ ｎｅｗ ａｌｇｏｒｉｔｈｍ ｋｎｏｗｎ ａｓ ｌａｂｅｌ ｄｉｓｔｒｉｂｕｔｉｏｎ ｌｅａｒｎｉｎｇ ｂａｓｅｄ ｏｎ ｋ⁃ｍｅａｎｓ ａｌｇｏｒｉｔｈｍ （ＬＤＬＫＭ） ｗａｓ ｐｒｏｐｏｓｅｄ． Ｉｔ ｆｉｒｓｔｌｙ ｃａｌｃｕｌａｔｅｄ ｅａｃｈ ｃｌｕｓｔｅｒ􀆳ｓ ｍｅａｎ ｖｅｃｔｏｒ ｕｓｉｎｇ ｔｈｅ ｋ⁃ｍｅａｎｓ ａｌｇｏｒｉｔｈｍ． Ｔｈｅｎ， ｉｔ ｇｏｔ ｔｈｅ ｍｅａｎ ｖｅｃｔｏｒ ｏｆ ｔｈｅ ｌａｂｅｌ ｄｉｓｔｒｉｂｕｔｉｏｎ ｃｏｒｒｅｓｐｏｎｄｉｎｇ ｔｏ ｔｈｅ ｔｒａｉｎｉｎｇ ｓｅｔ． Ｆｉｎａｌｌｙ， ｔｈｅ ｄｉｓｔａｎｃｅ ｂｅｔｗｅｅｎ ｔｈｅ ｍｅａｎ ｖｅｃｔｏｒｓ ｏｆ ｔｈｅ ｔｅｓｔ ｓｅｔ ａｎｄ ｔｈｅ ｔｒａｉｎｉｎｇ ｓｅｔ ｗａｓ ａｐｐｌｉｅｄ ｔｏ ｐｒｅｄｉｃｔ ｌａｂｅｌ ｄｉｓｔｒｉｂｕｔｉｏｎ ｏｆ ｔｈｅ ｔｅｓｔ ｓｅｔ ａｓ ａ ｗｅｉｇｈｔ． Ｅｘｐｅｒｉｍｅｎｔｓ ｗｅｒｅ ｃｏｎｄｕｃｔｅｄ ｏｎ ｓｉｘ ｐｕｂｌｉｃ ｄａｔａ ｓｅｔｓ ａｎｄ ｔｈｅｎ ｃｏｍｐａｒｅｄ ｗｉｔｈ ｔｈｒｅｅ ｅｘｉｓｔｉｎｇ ｌａｂｅｌ ｄｉｓｔｒｉｂｕｔｉｏｎ ｌｅａｒｎｉｎｇ ａｌｇｏｒｉｔｈｍｓ ｆｏｒ ｆｉｖｅ ｔｙｐｅｓ ｏｆ ｅｖａｌｕａｔｉｏｎ ｍｅａｓｕｒｅｓ． Ｔｈｅ ｅｘｐｅｒｉｍｅｎｔａｌ ｒｅｓｕｌｔｓ ｄｅｍｏｎｓｔｒａｔｅ ｔｈｅ ｅｆｆｅｃｔｉｖｅｎｅｓｓ ｏｆ ｔｈｅ ｐｒｏｐｏｓｅｄ ＫＭ⁃ＬＤＬ ａｌｇｏｒｉｔｈｍ． Ｋｅｙｗｏｒｄｓ：ｌａｂｅｌ ｄｉｓｔｒｉｂｕｔｉｏｎ； ｃｌｕｓｔｅｒｉｎｇ； ｋ⁃ｍｅａｎｓ； Ｍｉｎｋｏｗｓｋｉ ｄｉｓｔａｎｃｅ； ｍｕｌｔｉ⁃ｌａｂｅｌ； ｗｅｉｇｈｔ ｍａｔｒｉｘ； ｍｅａｎ ｖｅｃｔｏｒ； ｓｏｆｔｍａｘ ｆｕｎｃｔｉｏｎ 收稿日期：２０１７－０４－１９． 网络出版日期：２０１７－０７－０４． 基金项目：国家自然科学基金项目（６１３７９０４９， ６１３７９０８９）． 通信作者：杨文元． Ｅ⁃ｍａｉｌ：ｙａｎｇｗｙ＠ ｘｍｕ．ｅｄｕ．ｃｎ． 近年来，标记多义性问题是机器学习和数据挖 掘领域的热门问题。 目前已有的两种比较成熟的 学习范式是对每个实例分配单个标记的单标记学 习（ｓｉｎｇｌｅ⁃ｌａｂｅｌ ｌｅａｒｎｉｎｇ） 和对一个实例分配多个标 记的多标记学习（ｍｕｌｔｉ⁃ｌａｂｅｌ ｌｅａｒｎｉｎｇ） ［１］ 。 多标记学 习是对单标记学习的拓展［２］ 。 通常多标记学习能 处理一个实例属于多个标记的分歧情况。 通过大 量的研究和实验［３－５］ 表明，多标记学习是一种有效 且应用范围较广的学习范式。 多标记学习虽然对于一个实例允许标上多个

·326 智能系统学报 第12卷 标记，拓展了单标记学习。但是仍有一些问题是不 集时花费的时间较多。 太适合用多标记学习解决的，例如，标记集中的每 聚类4]是研究分类问题的一种统计分析方法， 一个标记描述实例的准确度是多少。事实上，现实 同时也是数据挖掘的一个重要算法，在研究过程中 世界中有着比大多数人想象的多得多的关于每个 也有许许多多的应用和改进)。聚类以相似性为 标记的准确描述度的数据。在许多科学实验中[6 基础，试图将数据集中的样本划分为若干个不相交 它们的输出结果不是单个值的，而是一系列的数值 的子集，每个子集称为一个簇，同一簇中样本之间 输出，例如，基因在不同时间点上的表达水平。这 的相似性比不在同一簇中的更高。在聚类算法中 些输出中的单个数值可能不是那么重要，真正重要 常用的k-means算法[16]及改进算法[7)是原型聚类 的是这一系列输出数值的分布情况。如果一个机 的一种，它假设聚类结构能通过一组原型刻画。通 器学习的任务是要预测一个数值分布，那么它很难 常情况下，算法先对原型进行初始化，然后对原型 放到多标记学习的框架中实现。因为在一个分布 进行迭代更新求解，直到均值向量不再改变或达到 中每一个数值输出的准确度是至关重要的，而且这 最大迭代次数，此时就能得到每一个簇的均值向量。 里也不再有相关标记与无关标记的区分了。因此， 在同一个数据集中，特征相近的实例，它们的 为了解决这类问题，Geng等)拓展了多标记学习， 标记分布往往也相似，同时依据聚类的特性，本文 提出了标记分布学习(label distribution learning, 提出一种新的标记分布算法：基于k-means的标记 LDL)范式。对于一个特定的实例，标记集合中所有 分布学习算法(label distribution learning algorithm 标记的描述度构建一个类似于概率分布的数据形 based on k-means,LDLKM)。首先，利用k-means聚 式，称之为标记分布⑧)，即每个训练实例与一个标 类算法求得训练样本集中每个簇的均值向量，此时 记分布相对应。与多标记学习输出一个标记集不 与每一个训练样本对应的标记分布也相应被划分 同，标记分布学习输出的是一个标记分布，分布中 成簇。然后，求得标记分布的每个簇的均值向量。 的每个分量表示对应标记对实例的描述程度。事 其次，测试集的样本到各个簇的均值向量的距离矩 实上，标记分布学习是一种适用场景更广的学习范 阵可通过常用的求距离方式，闵可夫斯基距离 式，能够解决更多的标记多义性问题。单标记学习 (Minkowski distance)Iu]求得。最后，将距离矩阵通 和多标记学习都可以看成标记分布学习的特例，相 过一个softmax函数变换得到一个权重矩阵。权重 关的研究成果[，o]也说明了这一点。 矩阵和训练样本集的标记分布的均值向量的积就 目前，已有一些标记分布学习算法[7，川被提了 是测试集样本的标记分布，即需要预测的标记分 出来。这些算法的设计策略主要可以分为以下 布。本文提出的LDLKM算法与现有的专用化的算 3类。 法相比并未采用条件概率的方式建立模型，而是充 1)问题转换，即将标记分布学习问题转换成单 分考虑了特征间的分布关系和特征与对应的标记 标记学习问题后，再利用相应范式中已有的算法进 分布之间的联系，利用k-means聚类和权重矩阵将 行求解，例如：PT-SVM算法和PT-Bayes算法。 特征和标记分布联系到一起。事实上，特征之间的 2)算法适应，即扩展现存的学习算法来处理标 分布与对应标记之间的分布的关系是一种更加直 签分布学习问题，例如：LDSVR[]算法和AA-BP 接和强烈的联系。而直接利用这种关系预测得到 算法。 的标记分布可以继续保持与对应特征的分布关系， 3)专用化的算法，即根据LDL的特点设计特殊 从而得到一个较好的结果。LDLKM和现有的3种 的算法，例如：SA-IS算法、CPNNU]和SA-BFGS LDL算法在6个公开数据集)上采用5种评价方式 算法。 进行实验比较，实验的结果表明本文提出的标记分 在这3种策略中，第3种直接针对标记分布学 布学习算法在使用的所有数据集上均取得较好的 习设计专门算法的效果是最好的。事实上，专用化 效果，在其中的5个数据集上所有评价方式的结果 的算法是通过条件概率或逻辑回归方式训练模型， 均为最优。 然后以这个模型预测想要的标记分布。但是在这 1标记分布学习的形式化 个过程中算法并未充分考虑训练实例与对应标记 分布之间的关系，例如：特征与标记间的函数关系， 在标记分布中，标记一个实例x的方式是为它 特征与标记间的分布关系和标记分布数据内部的 的每一个可能的标记y分配一个实数d,用来表示 分布关系。同时，现有的专门算法在处理较大数据 标记y对实例x的描述程度。不失一般性，假设实

标记，拓展了单标记学习。 但是仍有一些问题是不 太适合用多标记学习解决的，例如，标记集中的每 一个标记描述实例的准确度是多少。 事实上，现实 世界中有着比大多数人想象的多得多的关于每个 标记的准确描述度的数据。 在许多科学实验中［６］ ， 它们的输出结果不是单个值的，而是一系列的数值 输出，例如，基因在不同时间点上的表达水平。 这 些输出中的单个数值可能不是那么重要，真正重要 的是这一系列输出数值的分布情况。 如果一个机 器学习的任务是要预测一个数值分布，那么它很难 放到多标记学习的框架中实现。 因为在一个分布 中每一个数值输出的准确度是至关重要的，而且这 里也不再有相关标记与无关标记的区分了。 因此， 为了解决这类问题，Ｇｅｎｇ 等［７］ 拓展了多标记学习， 提出了标记分布学习 （ ｌａｂｅｌ ｄｉｓｔｒｉｂｕｔｉｏｎ ｌｅａｒｎｉｎｇ， ＬＤＬ）范式。 对于一个特定的实例，标记集合中所有 标记的描述度构建一个类似于概率分布的数据形 式，称之为标记分布［８］ ，即每个训练实例与一个标 记分布相对应。 与多标记学习输出一个标记集不 同，标记分布学习输出的是一个标记分布，分布中 的每个分量表示对应标记对实例的描述程度。 事 实上，标记分布学习是一种适用场景更广的学习范 式，能够解决更多的标记多义性问题。 单标记学习 和多标记学习都可以看成标记分布学习的特例，相 关的研究成果［７， ９－１０］也说明了这一点。 目前，已有一些标记分布学习算法［７， １１］ 被提了 出来。 这些算法的设计策略主要可以分为以下 ３ 类。 １）问题转换，即将标记分布学习问题转换成单 标记学习问题后，再利用相应范式中已有的算法进 行求解，例如：ＰＴ⁃ＳＶＭ 算法和 ＰＴ⁃Ｂａｙｅｓ 算法。 ２）算法适应，即扩展现存的学习算法来处理标 签分布学习问题， 例如： ＬＤＳＶＲ ［１２］ 算法和 ＡＡ⁃ＢＰ 算法。 ３）专用化的算法，即根据 ＬＤＬ 的特点设计特殊 的算 法， 例 如： ＳＡ⁃ＩＩＳ 算 法、 ＣＰＮＮ ［１３］ 和 ＳＡ⁃ＢＦＧＳ 算法。 在这 ３ 种策略中，第 ３ 种直接针对标记分布学 习设计专门算法的效果是最好的。 事实上，专用化 的算法是通过条件概率或逻辑回归方式训练模型， 然后以这个模型预测想要的标记分布。 但是在这 个过程中算法并未充分考虑训练实例与对应标记 分布之间的关系，例如：特征与标记间的函数关系， 特征与标记间的分布关系和标记分布数据内部的 分布关系。 同时，现有的专门算法在处理较大数据 集时花费的时间较多。 聚类［１４］是研究分类问题的一种统计分析方法， 同时也是数据挖掘的一个重要算法，在研究过程中 也有许许多多的应用和改进［１５］ 。 聚类以相似性为 基础，试图将数据集中的样本划分为若干个不相交 的子集，每个子集称为一个簇，同一簇中样本之间 的相似性比不在同一簇中的更高。 在聚类算法中 常用的 ｋ⁃ｍｅａｎｓ 算法［１６］ 及改进算法［１７］ 是原型聚类 的一种，它假设聚类结构能通过一组原型刻画。 通 常情况下，算法先对原型进行初始化，然后对原型 进行迭代更新求解，直到均值向量不再改变或达到 最大迭代次数，此时就能得到每一个簇的均值向量。 在同一个数据集中，特征相近的实例，它们的 标记分布往往也相似，同时依据聚类的特性，本文 提出一种新的标记分布算法：基于 ｋ⁃ｍｅａｎｓ 的标记 分布学习算法 （ ｌａｂｅｌ ｄｉｓｔｒｉｂｕｔｉｏｎ ｌｅａｒｎｉｎｇ ａｌｇｏｒｉｔｈｍ ｂａｓｅｄ ｏｎ ｋ⁃ｍｅａｎｓ，ＬＤＬＫＭ）。 首先，利用 ｋ⁃ｍｅａｎｓ 聚 类算法求得训练样本集中每个簇的均值向量，此时 与每一个训练样本对应的标记分布也相应被划分 成簇。 然后，求得标记分布的每个簇的均值向量。 其次，测试集的样本到各个簇的均值向量的距离矩 阵可通 过 常 用 的 求 距 离 方 式， 闵 可 夫 斯 基 距 离 （Ｍｉｎｋｏｗｓｋｉ ｄｉｓｔａｎｃｅ） ［１８］求得。 最后，将距离矩阵通 过一个 ｓｏｆｔｍａｘ 函数变换得到一个权重矩阵。 权重 矩阵和训练样本集的标记分布的均值向量的积就 是测试集样本的标记分布，即需要预测的标记分 布。 本文提出的 ＬＤＬＫＭ 算法与现有的专用化的算 法相比并未采用条件概率的方式建立模型，而是充 分考虑了特征间的分布关系和特征与对应的标记 分布之间的联系，利用 ｋ⁃ｍｅａｎｓ 聚类和权重矩阵将 特征和标记分布联系到一起。 事实上，特征之间的 分布与对应标记之间的分布的关系是一种更加直 接和强烈的联系。 而直接利用这种关系预测得到 的标记分布可以继续保持与对应特征的分布关系， 从而得到一个较好的结果。 ＬＤＬＫＭ 和现有的 ３ 种 ＬＤＬ 算法在 ６ 个公开数据集［７］上采用 ５ 种评价方式 进行实验比较，实验的结果表明本文提出的标记分 布学习算法在使用的所有数据集上均取得较好的 效果，在其中的 ５ 个数据集上所有评价方式的结果 均为最优。 １ 标记分布学习的形式化 在标记分布中，标记一个实例 ｘ 的方式是为它 的每一个可能的标记 ｙ 分配一个实数 ｄ ｙ ｘ，用来表示 标记 ｙ 对实例 ｘ 的描述程度。 不失一般性，假设实 ·３２６· 智 能 系 统 学 报 第 １２ 卷

第3期 邵东恒，等：应用k-neans算法实现标记分布学习 ·327· 数d!∈[0,1]，进一步假设所有标记能够完整地描 高。最小化式(2)并不容易，找到其最优解需考察 述实例，则∑d=1。 训练集H所有可能的簇划分，这是一个NP难20- 的问题。因此，k-means算法采用了贪心策略，通过 标记分布学习是一种更为灵活复杂的标记学 迭代优化来近似求解式(2)。 习范式，然而学习中更好的灵活性通常意味着更大 的输出空间。从单标记学习到多标记学习，再到 首先，聚类过程中在H中随机选择k个样本作 标记分布学习，学习过程的输出空间的维度变得越 为初始均值向量{μ12，…“}，可以通过下式： da=lx-u:‖2 (3) 来越大。更为详细地，对于标记集合中有c个不同 标记的学习问题，单标记学习的分类器有c个可能 计算训练集样本x与各均值向量4：(i=1,2,…,k) 的距离。根据距离最近的均值向量确定x:的簇 的输出，多标记学习的分类器有2-1个可能的输 出。对标记分布学习的分类器来讲，只要在满足 标记： 入y=arg minie[1,2.…分 (4) d∈[0,1]和∑d心=1这两个约束条件的前提下， 式中入，∈(1,2，…，k)表示样本的簇标记。将样 它的输出空间的维度可能是无穷大的1] 本x划入相应的簇，即 标记分布学习定义的实例矩阵为X= C=CU [x;] (5) [x1x2…xn],x∈R表示第i个实例，i=1,2,…,no 更新簇C,的均值向量。式(3)~式(5)这个过程不 给定对应标记矩阵Y=[y1y2…y],y表示第j个 断迭代直到当前均值向量保持不变或迭代次数达 标记，j=1,2,…,c:给定样本的标记分布集是D= 到所规定的最大次数。 [D,D2…D.],D=[dd…d]表示实例x:的标 其次，当迭代结束求出所要划分的聚类和对应 记分布集，d表示标记y对实例x:的描述度。基于 的均值向量后，便可以依据标记分布与训练样本集 此，标记分布学习的一个训练集能够表示为 的对应关系得到标记分布的簇划分和标记分布每 S={(x1,D1),(x2,D2),…,(xn,Dn)}。 个簇的均值向量“。同时利用常用的距离计算公式 目前的标记分布学习算法的输出模型是一个 “闵可夫斯基距离”公式，即 最大嫡模型)： dist(x,s)=(∑lxn-xP） (6) pl:0)=zn(0,✉） (1) 求得测试集每个样本与各个簇的均值向量的距离 式中：Z=∑exp(∑0wf(x)）是归一化因数；9。 矩阵T。闵可夫斯基距离是欧式距离的推广，具有 广泛的应用，当p=1时是曼哈顿距离，p=2就是欧 是模型参数；f(x)是x的第j个特征。随着标记分 布的发展逐渐提出许多基于式(1)的标记分布学习 式距离，而当p趋于无穷大时就是切比雪夫距离。 方法[7,9-o。这些算法先通过条件概率建立参数模 本文中将距离矩阵T的每个元素求倒数再通过一 个softmax函数进行处理转换，从而得到从训练集样 型，再利用现有的模型求解参数日。 本的标记分布的均值向量转化为预测标记分布的 2 基于k-means的标记分布学习算法 权重矩阵。对矩阵T作以下处理，先对T中每个元 素求导数： k-means算法是所有聚类算法中简单常用的一 种算法[0。它假设聚类结构能被一组原型刻画，先 1 (7) 初始化一组原型，然后对原型进行迭代更新求解， 然后，为了尽量减小与测试样本实例距离较远 最终得到每一个簇的均值向量。给定训练集H= 的均值向量的影响和便于之后的计算，利用softmax [x1x2…xm],m为训练集样本数。k-means算法针 对聚类所得簇划分G={C,C2,…,C},最小化平方 exp(x:) 函数Zk=softmax(xg)= 再作以下 误差为 ∑ep() E=Σ∑Ix-:I 处理： (2 exp(T') W。= a=1,2,…,n (8) 人∑x是簇C,的均值向量。直观来 式中：u:=C2 exp(T'au) 6=1 看，式(2)在一定程度上刻画了簇内样本围绕簇均 式中：n是测试集样本实例数，W为最后预测标记分 值向量的紧密程度，E值越小则簇内样本相似度越 布所使用的权重矩阵

数 ｄ ｙ ｘ∈ [０，１] ，进一步假设所有标记能够完整地描 述实例，则 ∑ｙ ｄ ｙ ｘ ＝ １。 标记分布学习是一种更为灵活复杂的标记学 习范式，然而学习中更好的灵活性通常意味着更大 的输出空间［１９］ 。 从单标记学习到多标记学习，再到 标记分布学习，学习过程的输出空间的维度变得越 来越大。 更为详细地，对于标记集合中有 ｃ 个不同 标记的学习问题，单标记学习的分类器有 ｃ 个可能 的输出，多标记学习的分类器有 ２ ｃ －１ 个可能的输 出。 对标记分布学习的分类器来讲，只要在满足 ｄ ｙ ｘ∈ [０，１] 和 ∑ｙ ｄ ｙ ｘ ＝ １ 这两个约束条件的前提下， 它的输出空间的维度可能是无穷大的［１９］ 。 标记 分 布 学 习 定 义 的 实 例 矩 阵 为 Ｘ ＝ ｘ１ ｘ２… ｘｎ [ ] ，ｘｉ∈Ｒ ｄ 表示第 ｉ 个实例，ｉ ＝ １，２，…，ｎ。 给定对应标记矩阵 Ｙ ＝ ｙ１ ｙ２… ｙｃ [ ] ，ｙｊ 表示第 ｊ 个 标记， ｊ ＝ １，２，…，ｃ；给定样本的标记分布集是 Ｄ ＝ Ｄ１ Ｄ２… Ｄｎ [ ] ，Ｄｉ ＝ ｄ ｙ１ ｘｉ ｄ ｙ２ ｘｉ … ｄ ｙｃ ｘｉ [ ] 表示实例 ｘｉ 的标 记分布集，ｄ ｙｊ ｘｉ表示标记 ｙｊ 对实例 ｘｉ 的描述度。 基于 此， 标 记 分 布 学 习 的 一 个 训 练 集 能 够 表 示 为 Ｓ ＝ （ｘ１ ，Ｄ１ ），（ｘ２ ，Ｄ２ ），…，（ｘ { ｎ ，Ｄｎ ）} 。 目前的标记分布学习算法的输出模型是一个 最大熵模型［７］ ： ｐ（ｙ ｘ；θ） ＝ １ Ｚ ｅｘｐ ∑ ｊ θｙ，ｊ ｆ ( ｊ（ｘ） ) （１） 式中： Ｚ ＝ ∑ｙ ｅｘｐ ∑ ｊ θｙ，ｊ ｆ ( ｊ（ｘ） ) 是归一化因数；θｙ，ｊ 是模型参数； ｆ ｊ（ｘ） 是 ｘ 的第 ｊ 个特征。 随着标记分 布的发展逐渐提出许多基于式（１） 的标记分布学习 方法［７，９－１０］ 。 这些算法先通过条件概率建立参数模 型，再利用现有的模型求解参数 θ。 ２ 基于 ｋ⁃ｍｅａｎｓ 的标记分布学习算法 ｋ－ｍｅａｎｓ 算法是所有聚类算法中简单常用的一 种算法［２０］ 。 它假设聚类结构能被一组原型刻画，先 初始化一组原型，然后对原型进行迭代更新求解， 最终得到每一个簇的均值向量。 给定训练集 Ｈ ＝ ｘ１ ｘ２… ｘｍ [ ] ，ｍ 为训练集样本数。 ｋ⁃ｍｅａｎｓ 算法针 对聚类所得簇划分 Ｇ ＝ Ｃ１ ，Ｃ２ ，…，Ｃｋ { } ，最小化平方 误差为 Ｅ ＝ ∑ ｋ ｉ ＝ １ ∑ｘ∈Ｃｉ ‖ｘ － μｉ‖２ ２ （２） 式中： μｉ ＝ １ Ｃｉ ∑ｘ∈Ｃｉ ｘ 是簇 Ｃｉ 的均值向量。 直观来 看，式（２） 在一定程度上刻画了簇内样本围绕簇均 值向量的紧密程度，Ｅ 值越小则簇内样本相似度越 高。 最小化式（２） 并不容易，找到其最优解需考察 训练集 Ｈ 所有可能的簇划分，这是一个 ＮＰ 难［２０－２１］ 的问题。 因此，ｋ⁃ｍｅａｎｓ 算法采用了贪心策略，通过 迭代优化来近似求解式（２）。 首先，聚类过程中在 Ｈ 中随机选择 ｋ 个样本作 为初始均值向量 μ１ ，μ２ ，…，μｋ { } ，可以通过下式： ｄｊｉ ＝ ‖ｘｊ － μｉ‖２ （３） 计算训练集样本 ｘｊ 与各均值向量 μｉ（ ｉ ＝ １，２，…，ｋ） 的距离。 根据距离最近的均值向量确定 ｘｊ 的簇 标记： λｊ ＝ ａｒｇ ｍｉｎｉ∈［１，２，…，ｋ］ ｄｊｉ （４） 式中 λｊ∈(１，２，…，ｋ) 表示样本 ｘｊ 的簇标记。 将样 本 ｘｊ 划入相应的簇，即 Ｃλｊ ＝ Ｃλｊ ∪ ［ｘｊ］ （５） 更新簇 Ｃλｊ的均值向量。 式（３） ～ 式（５）这个过程不 断迭代直到当前均值向量保持不变或迭代次数达 到所规定的最大次数。 其次，当迭代结束求出所要划分的聚类和对应 的均值向量后，便可以依据标记分布与训练样本集 的对应关系得到标记分布的簇划分和标记分布每 个簇的均值向量 ｕ。 同时利用常用的距离计算公式 “闵可夫斯基距离”公式，即 ｄｉｓｔｍｋ（ｘｉ，ｘｊ） ＝ ∑ ｎ ｕ ＝ １ ｘｉｕ － ｘｊｕ ｐ ( ) １ ｐ （６） 求得测试集每个样本与各个簇的均值向量的距离 矩阵 Ｔ。 闵可夫斯基距离是欧式距离的推广，具有 广泛的应用，当 ｐ ＝ １ 时是曼哈顿距离，ｐ ＝ ２ 就是欧 式距离，而当 ｐ 趋于无穷大时就是切比雪夫距离。 本文中将距离矩阵 Ｔ 的每个元素求倒数再通过一 个 ｓｏｆｔｍａｘ 函数进行处理转换，从而得到从训练集样 本的标记分布的均值向量转化为预测标记分布的 权重矩阵。 对矩阵 Ｔ 作以下处理，先对 Ｔ 中每个元 素求导数： Ｔ′ａｂ ＝ １ Ｔａｂ （７） 然后，为了尽量减小与测试样本实例距离较远 的均值向量的影响和便于之后的计算，利用 ｓｏｆｔｍａｘ 函数 Ｚｋ ＝ ｓｏｆｔｍａｘ（ｘｋ） ＝ ｅｘｐ（ｘｋ） ∑ ｋ ｉ ＝ １ ｅｘｐ（ｘｉ） 再作以下 处理： Ｗａ ＝ ｅｘｐ（Ｔ′ａｂ） ∑ ｋ ｂ ＝ １ ｅｘｐ（Ｔ′ａｂ） ， ａ ＝ １，２，…，ｎ （８） 式中：ｎ 是测试集样本实例数，Ｗ 为最后预测标记分 布所使用的权重矩阵。 第 ３ 期 邵东恒，等：应用 ｋ⁃ｍｅａｎｓ 算法实现标记分布学习 ·３２７·

·328 智能系统学报 第12卷 最后将W与训练集对应的标记分布的均值向 8)根据式(9)得出预测标记分布P。 量矩阵U相乘，即 实验与结果分析 P=WU (9) 式中：U=[u12…u,];P就是所需要求的预测标记 在这部分，将通过实验来验证本文提出的基于 分布。 k-means的标记分布学习算法。 上述的算法过程可以通过图1的流程图来 标记分布学习算法的输出是一个标记分布，与 表示。 单标记学习的单标记输出和多标记学习的标记集 输入 输出都不同。因此，标记分布学习算法的评价方 式，应该与单标记学习和多标记学习算法不同。这 [选择初始均值向量 种方式不是通过预测标记的准确度来评价算法优 计算样本与均值向量的距离 劣，而是通过测量预测结果和真实标记分布之间的 划分样本筷 距离或相似度来衡量算法效果。有很多测量概率 分布之间的距离或相似度的方法)可以用来很好 更新均值向量 地测量标记分布之间的距离或相似度。例如，表1 <是否更新一 Y 中根据文献[7]和[22]选出的5种测量方式就能很 N 好地用来评价标记分布算法。评价标准距离名称 样本到均值向量的距离矩阵 之后的“↓”代表距离值越小越好，相似度名称之后 预测标记分布权重矩阵 的“↑”表示相似值越大越好。这5种评价方法分 别是切比雪夫距离(Chebyshev)、克拉克距离 (输出预测标记分布○ (Clark)、堪培拉量度(Canberra)、弦系数(Cosine)以 图1 LDLKM算法流程图 及交叉相似性(Intersection),前3种以距离作为评 Fig.1 The flowchart of LDLKM 价，即越小越好，后两种以相似度作为评价，即越大 本文提出的LDLKM算法具体步骤如下： 越好。 算法基于k-means算法的标记分布学习 表1评价指标 (LDLKM)。 Table 1 Evaluation index 输入聚类的簇数k,聚类迭代的最大次数d,闵可 评价标准 计算形式 夫斯基距离参数P,训练集S={(x1,D),(x2,D2),…, Chebyshev↓ (x,D) Dis,=maxdd 输出测试集的预测标记分布P。 1)从训练集样本H中随机选择k个样本作为 (d,-4,)月 Clark↓ Dis,= 初始向量{u1,u2,…,“}。 V(d.d) 2)迭代开始，令C,(1≤i≤k)为空，利用式(3)】 计算样本x与各均值向量u:的距离。 Canberra↓ 3)依据式(4)，根据距离最近的均值向量确定 ,=刻 d,d x的簇标记入；将样本x,划入相应的簇。 4)更新均值向量，分别计算划分完簇后的新的 ∑4d Cosine Dis, 均简向量：，向三。 √G√∑话 5)若当前的均值向量均未更新或达到规定的 Intersection↑ Dis5=∑i.1min(d,d） 最大迭代次数，继续下一步：否则，返回2)，重复3) 到5)直到所有测法样本划分完毕。 3.1实验设置 6)依据式(6)求得测试集每个样本与各个均值 通过上述5种评价方式，本次实验在6个公开 向量的距离矩阵T。 的数据集上进行，它们分别是Yeast-.alpha、Yeast- 7)利用式(7)和式(8)求得预测标记分布的权 cdc、Yeast--elu、SJAFFE、Human Gene和Movie,详 重矩阵W。 细的信息如表2所示

最后将 Ｗ 与训练集对应的标记分布的均值向 量矩阵 Ｕ 相乘，即 Ｐ ＝ ＷＵ （９） 式中：Ｕ ＝ ［ｕ１ ｕ２… ｕｂ］；Ｐ 就是所需要求的预测标记 分布。 上述的算法过程可以通过图 １ 的流程图来 表示。 图 １ ＬＤＬＫＭ 算法流程图 Ｆｉｇ．１ Ｔｈｅ ｆｌｏｗｃｈａｒｔ ｏｆ ＬＤＬＫＭ 本文提出的 ＬＤＬＫＭ 算法具体步骤如下： 算法 基 于 ｋ⁃ｍｅａｎｓ 算 法 的 标 记 分 布 学 习 （ＬＤＬＫＭ）。 输入 聚类的簇数 ｋ，聚类迭代的最大次数 ｄ，闵可 夫斯基距离参数 ｐ，训练集 Ｓ ＝｛（ｘ１，Ｄ１ ），（ｘ２，Ｄ２ ），…， （ｘｎ，Ｄｎ）｝。 输出 测试集的预测标记分布 Ｐ。 １）从训练集样本 Ｈ 中随机选择 ｋ 个样本作为 初始向量 μ１ ， μ２ ， …， μｋ { } 。 ２）迭代开始，令 Ｃｉ（１≤ｉ≤ｋ）为空，利用式（３） 计算样本 ｘｊ 与各均值向量 μｉ 的距离。 ３）依据式（４），根据距离最近的均值向量确定 ｘｊ 的簇标记 λｊ；将样本 ｘｊ 划入相应的簇。 ４）更新均值向量，分别计算划分完簇后的新的 均值向量： μｉ ＝ １ Ｃｉ ∑ｘ∈Ｃｉ ｘ。 ５）若当前的均值向量均未更新或达到规定的 最大迭代次数，继续下一步；否则，返回 ２），重复 ３） 到 ５）直到所有测法样本划分完毕。 ６）依据式（６）求得测试集每个样本与各个均值 向量的距离矩阵 Ｔ。 ７）利用式（７）和式（８）求得预测标记分布的权 重矩阵 Ｗ。 ８）根据式（９）得出预测标记分布 Ｐ。 ３ 实验与结果分析 在这部分，将通过实验来验证本文提出的基于 ｋ⁃ｍｅａｎｓ 的标记分布学习算法。 标记分布学习算法的输出是一个标记分布，与 单标记学习的单标记输出和多标记学习的标记集 输出都不同。 因此，标记分布学习算法的评价方 式，应该与单标记学习和多标记学习算法不同。 这 种方式不是通过预测标记的准确度来评价算法优 劣，而是通过测量预测结果和真实标记分布之间的 距离或相似度来衡量算法效果。 有很多测量概率 分布之间的距离或相似度的方法［７］ 可以用来很好 地测量标记分布之间的距离或相似度。 例如，表 １ 中根据文献［７］和［２２］选出的 ５ 种测量方式就能很 好地用来评价标记分布算法。 评价标准距离名称 之后的“↓”代表距离值越小越好，相似度名称之后 的“↑”表示相似值越大越好。 这 ５ 种评价方法分 别是 切 比 雪 夫 距 离 （ Ｃｈｅｂｙｓｈｅｖ ）、 克 拉 克 距 离 （Ｃｌａｒｋ）、堪培拉量度（Ｃａｎｂｅｒｒａ）、弦系数（Ｃｏｓｉｎｅ）以 及交叉相似性（ Ｉｎｔｅｒｓｅｃｔｉｏｎ），前 ３ 种以距离作为评 价，即越小越好，后两种以相似度作为评价，即越大 越好。 表 １ 评价指标 Ｔａｂｌｅ １ Ｅｖａｌｕａｔｉｏｎ ｉｎｄｅｘ 评价标准 计算形式 Ｃｈｅｂｙｓｈｅｖ ↓ Ｄｉｓ１ ＝ｍａｘ ｌ ｄｌ －ｄ ∧ ｌ Ｃｌａｒｋ ↓ Ｄｉｓ２ ＝ ∑ｃ ｌ＝ １ （ｄｌ －ｄ ∧ ｌ） ２ （ｄｌ，ｄ ∧ ｌ） ２ Ｃａｎｂｅｒｒａ ↓ Ｄｉｓ３ ＝ ∑ ｃ ｌ ＝ １ ｄｌ － ｄｌ ∧ ｄｌ ＋ ｄｌ ∧ Ｃｏｓｉｎｅ ↑ Ｄｉｓ４ ＝ ∑ ｃ ｌ ＝ １ ｄｌ ｄｌ ∧ ∑ ｃ ｌ ＝ １ ｄ ２ ｌ ∑ ｃ ｌ ＝ １ ｄ ２ ｌ ∧ Ｉｎｔｅｒｓｅｃｔｉｏｎ ↑ Ｄｉｓ５ ＝∑ｃ ｌ＝ １ｍｉｎ（ｄｌ，ｄｌ ∧ ） ３．１ 实验设置 通过上述 ５ 种评价方式，本次实验在 ６ 个公开 的数据集上进行，它们分别是 Ｙｅａｓｔ⁃ａｌｐｈａ、 Ｙｅａｓｔ⁃ ｃｄｃ、 Ｙｅａｓｔ⁃ｅｌｕ、 ＳＪＡＦＦＥ、 Ｈｕｍａｎ Ｇｅｎｅ 和 Ｍｏｖｉｅ，详 细的信息如表 ２ 所示。 ·３２８· 智 能 系 统 学 报 第 １２ 卷

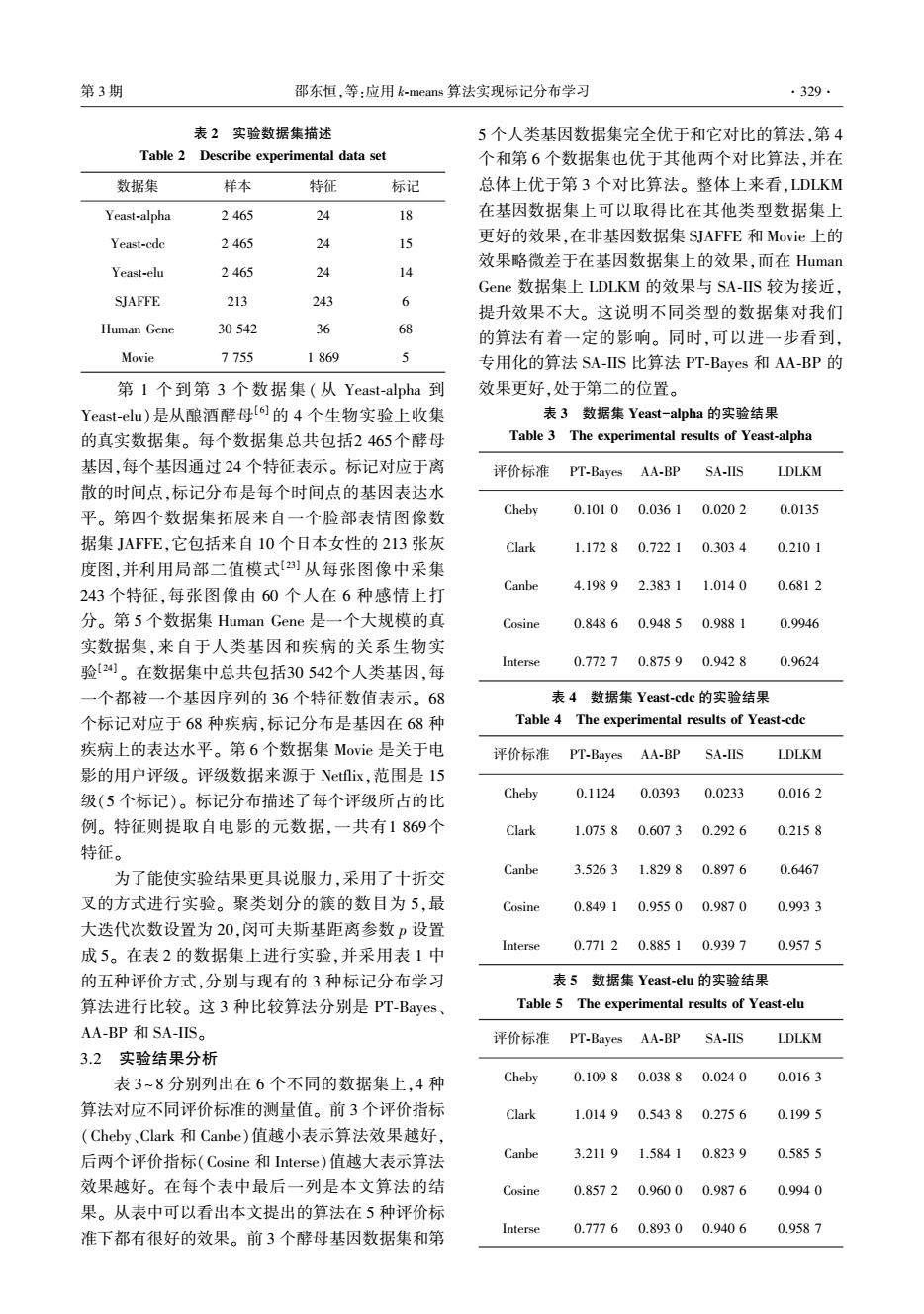
第3期 邵东恒，等：应用k-means算法实现标记分布学习 ·329· 表2实验数据集描述 5个人类基因数据集完全优于和它对比的算法，第4 Table 2 Describe experimental data set 个和第6个数据集也优于其他两个对比算法，并在 数据集 样本 特征 标记 总体上优于第3个对比算法。整体上来看，LDLKM Yeast-alpha 2465 24 18 在基因数据集上可以取得比在其他类型数据集上 Yeast-cde 2465 24 15 更好的效果，在非基因数据集SJAFFE和Movie上的 效果略微差于在基因数据集上的效果，而在Human Yeast-elu 2465 24 14 Gene数据集上LDLKM的效果与SA-IIS较为接近， SJAFFE 213 243 6 提升效果不大。这说明不同类型的数据集对我们 Human Gene 30542 36 68 的算法有着一定的影响。同时，可以进一步看到， Movie 7755 1869 J 专用化的算法SA-IIS比算法PT-Bayes和AA-BP的 第1个到第3个数据集（从Yeast-alpha到 效果更好，处于第二的位置。 Yeast-elu)是从酿酒酵母6的4个生物实验上收集 表3数据集Yeast--alpha的实验结果 的真实数据集。每个数据集总共包括2465个酵母 Table 3 The experimental results of Yeast-alpha 基因，每个基因通过24个特征表示。标记对应于离 评价标准PT-Bayes AA-BP SA-IIS LDLKM 散的时间点，标记分布是每个时间点的基因表达水 平。第四个数据集拓展来自一个脸部表情图像数 Cheby 0.1010 0.0361 0.0202 0.0135 据集JAF℉E,它包括来自10个日本女性的213张灰 Clark 1.17280.7221 0.3034 0.2101 度图，并利用局部二值模式]从每张图像中采集 Canbe 4.1989 2.3831 1.0140 243个特征，每张图像由60个人在6种感情上打 0.6812 分。第5个数据集Human Gene是一个大规模的真 Cosine 0.8486 0.9485 0.9881 0.9946 实数据集，来自于人类基因和疾病的关系生物实 验[24】。在数据集中总共包括30542个人类基因，每 Interse 0.7727 0.8759 0.9428 0.9624 一个都被一个基因序列的36个特征数值表示。68 表4数据集Yeast-.cdc的实验结果 个标记对应于68种疾病，标记分布是基因在68种 Table 4 The experimental results of Yeast-cdc 疾病上的表达水平。第6个数据集Movie是关于电 评价标准 PT-Bayes AA-BP SA-IIS LDLKM 影的用户评级。评级数据来源于Netflix,范围是15 级(5个标记)。标记分布描述了每个评级所占的比 Cheby 0.1124 0.0393 0.0233 0.0162 例。特征则提取自电影的元数据，一共有1869个 Clark 1.0758 0.6073 0.2926 0.2158 特征。 为了能使实验结果更具说服力，采用了十折交 Canbe 3.5263 1.8298 0.8976 0.6467 叉的方式进行实验。聚类划分的簇的数目为5，最 Cosine 0.8491 0.95500.9870 0.9933 大迭代次数设置为20，闵可夫斯基距离参数p设置 成5。在表2的数据集上进行实验，并采用表1中 Interse 0.77120.8851 0.9397 0.9575 的五种评价方式，分别与现有的3种标记分布学习 表5数据集Yeast-.elu的实验结果 算法进行比较。这3种比较算法分别是PT-Bayes、 Table 5 The experimental results of Yeast-elu AA-BP和SA-IIS。 评价标准 PT-Bayes AA-BP SA-IIS LDLKM 3.2实验结果分析 表3~8分别列出在6个不同的数据集上，4种 Cheby 0.1098 0.0388 0.0240 0.0163 算法对应不同评价标准的测量值。前3个评价指标 Clark 1.01490.5438 0.2756 0.1995 (Cheby、Clark和Canbe)值越小表示算法效果越好， 后两个评价指标(Cosine和Interse)值越大表示算法 Canbe 3.2119 1.5841 0.8239 0.5855 效果越好。在每个表中最后一列是本文算法的结 Cosine 0.85720.9600 0.9876 0.9940 果。从表中可以看出本文提出的算法在5种评价标 准下都有很好的效果。前3个酵母基因数据集和第 Interse 0.77760.89300.9406 0.9587

表 ２ 实验数据集描述 Ｔａｂｌｅ ２ Ｄｅｓｃｒｉｂｅ ｅｘｐｅｒｉｍｅｎｔａｌ ｄａｔａ ｓｅｔ 数据集 样本 特征 标记 Ｙｅａｓｔ⁃ａｌｐｈａ ２ ４６５ ２４ １８ Ｙｅａｓｔ⁃ｃｄｃ ２ ４６５ ２４ １５ Ｙｅａｓｔ⁃ｅｌｕ ２ ４６５ ２４ １４ ＳＪＡＦＦＥ ２１３ ２４３ ６ Ｈｕｍａｎ Ｇｅｎｅ ３０ ５４２ ３６ ６８ Ｍｏｖｉｅ ７ ７５５ １ ８６９ ５ 第 １ 个到第 ３ 个数据集 （ 从 Ｙｅａｓｔ⁃ａｌｐｈａ 到 Ｙｅａｓｔ⁃ｅｌｕ）是从酿酒酵母［６］ 的 ４ 个生物实验上收集 的真实数据集。 每个数据集总共包括２ ４６５个酵母 基因，每个基因通过 ２４ 个特征表示。 标记对应于离 散的时间点，标记分布是每个时间点的基因表达水 平。 第四个数据集拓展来自一个脸部表情图像数 据集 ＪＡＦＦＥ，它包括来自 １０ 个日本女性的 ２１３ 张灰 度图，并利用局部二值模式［２３］ 从每张图像中采集 ２４３ 个特征，每张图像由 ６０ 个人在 ６ 种感情上打 分。 第 ５ 个数据集 Ｈｕｍａｎ Ｇｅｎｅ 是一个大规模的真 实数据集，来自于人类基因和疾病的关系生物实 验［２４］ 。 在数据集中总共包括３０ ５４２个人类基因，每 一个都被一个基因序列的 ３６ 个特征数值表示。 ６８ 个标记对应于 ６８ 种疾病，标记分布是基因在 ６８ 种 疾病上的表达水平。 第 ６ 个数据集 Ｍｏｖｉｅ 是关于电 影的用户评级。 评级数据来源于 Ｎｅｔｆｌｉｘ，范围是 １５ 级（５ 个标记）。 标记分布描述了每个评级所占的比 例。 特征则提取自电影的元数据，一共有１ ８６９个 特征。 为了能使实验结果更具说服力，采用了十折交 叉的方式进行实验。 聚类划分的簇的数目为 ５，最 大迭代次数设置为 ２０，闵可夫斯基距离参数 ｐ 设置 成 ５。 在表 ２ 的数据集上进行实验，并采用表 １ 中 的五种评价方式，分别与现有的 ３ 种标记分布学习 算法进行比较。 这 ３ 种比较算法分别是 ＰＴ⁃Ｂａｙｅｓ、 ＡＡ⁃ＢＰ 和 ＳＡ⁃ＩＩＳ。 ３．２ 实验结果分析 表 ３～８ 分别列出在 ６ 个不同的数据集上，４ 种 算法对应不同评价标准的测量值。 前 ３ 个评价指标 （Ｃｈｅｂｙ、Ｃｌａｒｋ 和 Ｃａｎｂｅ）值越小表示算法效果越好， 后两个评价指标（Ｃｏｓｉｎｅ 和 Ｉｎｔｅｒｓｅ）值越大表示算法 效果越好。 在每个表中最后一列是本文算法的结 果。 从表中可以看出本文提出的算法在 ５ 种评价标 准下都有很好的效果。 前 ３ 个酵母基因数据集和第 ５ 个人类基因数据集完全优于和它对比的算法，第 ４ 个和第 ６ 个数据集也优于其他两个对比算法，并在 总体上优于第 ３ 个对比算法。 整体上来看，ＬＤＬＫＭ 在基因数据集上可以取得比在其他类型数据集上 更好的效果，在非基因数据集 ＳＪＡＦＦＥ 和 Ｍｏｖｉｅ 上的 效果略微差于在基因数据集上的效果，而在 Ｈｕｍａｎ Ｇｅｎｅ 数据集上 ＬＤＬＫＭ 的效果与 ＳＡ⁃ＩＩＳ 较为接近， 提升效果不大。 这说明不同类型的数据集对我们 的算法有着一定的影响。 同时，可以进一步看到， 专用化的算法 ＳＡ⁃ＩＩＳ 比算法 ＰＴ⁃Ｂａｙｅｓ 和 ＡＡ⁃ＢＰ 的 效果更好，处于第二的位置。 表 ３ 数据集 Ｙｅａｓｔ－ａｌｐｈａ 的实验结果 Ｔａｂｌｅ ３ Ｔｈｅ ｅｘｐｅｒｉｍｅｎｔａｌ ｒｅｓｕｌｔｓ ｏｆ Ｙｅａｓｔ⁃ａｌｐｈａ 评价标准 ＰＴ⁃Ｂａｙｅｓ ＡＡ⁃ＢＰ ＳＡ⁃ＩＩＳ ＬＤＬＫＭ Ｃｈｅｂｙ ０．１０１ ０ ０．０３６ １ ０．０２０ ２ ０．０１３５ Ｃｌａｒｋ １．１７２ ８ ０．７２２ １ ０．３０３ ４ ０．２１０ １ Ｃａｎｂｅ ４．１９８ ９ ２．３８３ １ １．０１４ ０ ０．６８１ ２ Ｃｏｓｉｎｅ ０．８４８ ６ ０．９４８ ５ ０．９８８ １ ０．９９４６ Ｉｎｔｅｒｓｅ ０．７７２ ７ ０．８７５ ９ ０．９４２ ８ ０．９６２４ 表 ４ 数据集 Ｙｅａｓｔ⁃ｃｄｃ 的实验结果 Ｔａｂｌｅ ４ Ｔｈｅ ｅｘｐｅｒｉｍｅｎｔａｌ ｒｅｓｕｌｔｓ ｏｆ Ｙｅａｓｔ⁃ｃｄｃ 评价标准 ＰＴ⁃Ｂａｙｅｓ ＡＡ⁃ＢＰ ＳＡ⁃ＩＩＳ ＬＤＬＫＭ Ｃｈｅｂｙ ０．１１２４ ０．０３９３ ０．０２３３ ０．０１６ ２ Ｃｌａｒｋ １．０７５ ８ ０．６０７ ３ ０．２９２ ６ ０．２１５ ８ Ｃａｎｂｅ ３．５２６ ３ １．８２９ ８ ０．８９７ ６ ０．６４６７ Ｃｏｓｉｎｅ ０．８４９ １ ０．９５５ ０ ０．９８７ ０ ０．９９３ ３ Ｉｎｔｅｒｓｅ ０．７７１ ２ ０．８８５ １ ０．９３９ ７ ０．９５７ ５ 表 ５ 数据集 Ｙｅａｓｔ⁃ｅｌｕ 的实验结果 Ｔａｂｌｅ ５ Ｔｈｅ ｅｘｐｅｒｉｍｅｎｔａｌ ｒｅｓｕｌｔｓ ｏｆ Ｙｅａｓｔ⁃ｅｌｕ 评价标准 ＰＴ⁃Ｂａｙｅｓ ＡＡ⁃ＢＰ ＳＡ⁃ＩＩＳ ＬＤＬＫＭ Ｃｈｅｂｙ ０．１０９ ８ ０．０３８ ８ ０．０２４ ０ ０．０１６ ３ Ｃｌａｒｋ １．０１４ ９ ０．５４３ ８ ０．２７５ ６ ０．１９９ ５ Ｃａｎｂｅ ３．２１１ ９ １．５８４ １ ０．８２３ ９ ０．５８５ ５ Ｃｏｓｉｎｅ ０．８５７ ２ ０．９６０ ０ ０．９８７ ６ ０．９９４ ０ Ｉｎｔｅｒｓｅ ０．７７７ ６ ０．８９３ ０ ０．９４０ ６ ０．９５８ ７ 第 ３ 期 邵东恒，等：应用 ｋ⁃ｍｅａｎｓ 算法实现标记分布学习 ·３２９·