【知识工程】基于粗糙集相对分类信息熵和粒子群优化的特征选择方法

第12卷第3期 智能系统学报 Vol.12 No.3 2017年6月 CAAI Transactions on Intelligent Systems Jun.2017 D0I:10.11992/is.201705004 网络出版地址：http:/kns.cmki.net/kcms/detail/23.1538.TP.20170703.1854.018.html 基于粗糙集相对分类信息熵和 粒子群优化的特征选择方法 翟俊海12，刘博3，张素芳4 (1.河北大学河北省机器学习与计算智能重点实验室，河北保定071002：2.浙江师范大学数理与信息工程学院，浙 江金华321004：3.河北大学计算机科学与技术学院，河北保定071002：4.中国气象局气象干部培训学院河北分 院，河北保定071000) 摘要：特征选择是指从初始特征全集中，依据既定规则筛选出特征子集的过程，是数据挖掘的重要预处理步骤。 通过剔除冗余属性，以达到降低算法复杂度和提高算法性能的目的。针对离散值特征选择问题，提出了一种将粗糙 集相对分类信息嫡和粒子群算法相结合的特征选择方法，依托粒子群算法，以相对分类信息嫡作为适应度函数，并 与其他基于进化算法的特征选择方法进行了实验比较，实验结果表明本文提出的方法具有一定的优势。 关键词：数据挖掘：特征选择：数据预处理：粗糙集：决策表：粒子群算法：信息嫡：适应度函数 中图分类号：TP181文献标志码：A文章编号：1673-4785(2017)03-0397-08 中文引用格式：翟俊海，刘博，张素芳.基于粗糙集相对分类信息熵和粒子群优化的特征选择方法[J].智能系统学报，2017,12(3)： 397-404. 英文引用格式：ZHAI Junhai,LIU Bo,ZHANG Sufang.A feature selection approach based on rough set relative classification information entropy and particle swarm optimization[.CAAI transactions on intelligent systems,2017,12(3):397-404. A feature selection approach based on rough set relative classification information entropy and particle swarm optimization ZHAI Junhai2,LIU Bo3,ZHANG Sufang" (1.Key Lab of Machine Learning and Computational Intelligence,Hebei University,Baoding 071002,China;2.College of Mathematics,Physics and Information Engineering,Zhejiang Normal University,Jinhua 321004,China;3.College of Computer Science and Technology,Hebei University,Baoding 071002,China;4.Hebei Branch of Meteorological Cadres Training Institute, China Meteorological Administration,Baoding 071000,China) Abstract:Feature selection,an important step in data mining,is a process that selects a subset from an original feature set based on some criteria.Its purpose is to reduce the computational complexity of the learning algorithm and to improve the performance of data mining by removing irrelevant and redundant features.To deal with the problem of discrete values,a feature selection approach was proposed in this paper.It uses a particle swarm optimization algorithm to search the optimal feature subset.Further,it employs relative classification information entropy as a fitness function to measure the significance of the feature subset.Then,the proposed approach was compared with other evolutionary algorithm-based methods of feature selection.The experimental results confirm that the proposed approach outperforms genetic algorithm-based methods. Keywords:data mining;feature selection;data preprocessing;rough set;decision table;particle swarm optimization;information entropy;fitness function 特征选择1-]是数据挖掘的重要预处理步骤， 集的评价准则或启发式确定后，特征选择问题从某 通过删除不必要特征，以达到降低算法复杂度，提 种意义上来说就是在特征空间中搜索最优特征子 高算法的性能。特征子集的评价至关重要，特征子 集问题。研究人员提出了许多特征选择算法，这些 算法有的是从设计特征子集搜索的方法考虑的，有 收稿日期：2017-05-07.网络出版日期：2017-07-03. 基金项目：国家自然科学基金项目(71371063)：河北省自然科学基金的是从设计评价特征子集重要性的度量考虑的。 项目(F2017201026):浙江省计算机科学与技术重中之重学 科（浙江师范大学）资助项目. 特征选择方法主要有筛选法(6 ilter method)、封 通信作者：翟俊海.E-mail:mcjh@126.com

第 １２ 卷第 ３ 期 智 能 系 统 学 报 Ｖｏｌ．１２ №．３ ２０１７ 年 ６ 月 ＣＡＡＩ Ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ Ｉｎｔｅｌｌｉｇｅｎｔ Ｓｙｓｔｅｍｓ Ｊｕｎ． ２０１７ ＤＯＩ：１０．１１９９２ ／ ｔｉｓ． ２０１７０５００４ 网络出版地址：ｈｔｔｐ： ／ ／ ｋｎｓ．ｃｎｋｉ．ｎｅｔ ／ ｋｃｍｓ／ ｄｅｔａｉｌ ／ ２３．１５３８．ＴＰ．２０１７０７０３．１８５４．０１８．ｈｔｍｌ 基于粗糙集相对分类信息熵和 粒子群优化的特征选择方法 翟俊海１， ２ ， 刘博３ ， 张素芳４ （１．河北大学 河北省机器学习与计算智能重点实验室，河北 保定 ０７１００２； ２． 浙江师范大学 数理与信息工程学院，浙 江 金华 ３２１００４； ３． 河北大学 计算机科学与技术学院，河北 保定 ０７１００２； ４． 中国气象局 气象干部培训学院河北分 院，河北 保定 ０７１０００） 摘 要：特征选择是指从初始特征全集中，依据既定规则筛选出特征子集的过程，是数据挖掘的重要预处理步骤。 通过剔除冗余属性，以达到降低算法复杂度和提高算法性能的目的。 针对离散值特征选择问题，提出了一种将粗糙 集相对分类信息熵和粒子群算法相结合的特征选择方法，依托粒子群算法，以相对分类信息熵作为适应度函数，并 与其他基于进化算法的特征选择方法进行了实验比较，实验结果表明本文提出的方法具有一定的优势。 关键词：数据挖掘；特征选择；数据预处理；粗糙集；决策表；粒子群算法；信息熵；适应度函数 中图分类号：ＴＰ１８１ 文献标志码：Ａ 文章编号：１６７３－４７８５（２０１７）０３－０３９７－０８ 中文引用格式：翟俊海，刘博，张素芳．基于粗糙集相对分类信息熵和粒子群优化的特征选择方法［Ｊ］． 智能系统学报， ２０１７， １２（３）： ３９７－４０４． 英文引用格式：ＺＨＡＩ Ｊｕｎｈａｉ，ＬＩＵ Ｂｏ，ＺＨＡＮＧ Ｓｕｆａｎｇ． Ａ ｆｅａｔｕｒｅ ｓｅｌｅｃｔｉｏｎ ａｐｐｒｏａｃｈ ｂａｓｅｄ ｏｎ ｒｏｕｇｈ ｓｅｔ ｒｅｌａｔｉｖｅ ｃｌａｓｓｉｆｉｃａｔｉｏｎ ｉｎｆｏｒｍａｔｉｏｎ ｅｎｔｒｏｐｙ ａｎｄ ｐａｒｔｉｃｌｅ ｓｗａｒｍ ｏｐｔｉｍｉｚａｔｉｏｎ［Ｊ］． ＣＡＡＩ ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ ｉｎｔｅｌｌｉｇｅｎｔ ｓｙｓｔｅｍｓ， ２０１７， １２（３）： ３９７－４０４． Ａ ｆｅａｔｕｒｅ ｓｅｌｅｃｔｉｏｎ ａｐｐｒｏａｃｈ ｂａｓｅｄ ｏｎ ｒｏｕｇｈ ｓｅｔ ｒｅｌａｔｉｖｅ ｃｌａｓｓｉｆｉｃａｔｉｏｎ ｉｎｆｏｒｍａｔｉｏｎ ｅｎｔｒｏｐｙ ａｎｄ ｐａｒｔｉｃｌｅ ｓｗａｒｍ ｏｐｔｉｍｉｚａｔｉｏｎ ＺＨＡＩ Ｊｕｎｈａｉ １，２ ， ＬＩＵ Ｂｏ ３ ， ＺＨＡＮＧ Ｓｕｆａｎｇ ４ （１． Ｋｅｙ Ｌａｂ ｏｆ Ｍａｃｈｉｎｅ Ｌｅａｒｎｉｎｇ ａｎｄ Ｃｏｍｐｕｔａｔｉｏｎａｌ Ｉｎｔｅｌｌｉｇｅｎｃｅ， Ｈｅｂｅｉ Ｕｎｉｖｅｒｓｉｔｙ， Ｂａｏｄｉｎｇ ０７１００２， Ｃｈｉｎａ； ２． Ｃｏｌｌｅｇｅ ｏｆ Ｍａｔｈｅｍａｔｉｃｓ， Ｐｈｙｓｉｃｓ ａｎｄ Ｉｎｆｏｒｍａｔｉｏｎ Ｅｎｇｉｎｅｅｒｉｎｇ， Ｚｈｅｊｉａｎｇ Ｎｏｒｍａｌ Ｕｎｉｖｅｒｓｉｔｙ， Ｊｉｎｈｕａ ３２１００４， Ｃｈｉｎａ； ３． Ｃｏｌｌｅｇｅ ｏｆ Ｃｏｍｐｕｔｅｒ Ｓｃｉｅｎｃｅ ａｎｄ Ｔｅｃｈｎｏｌｏｇｙ， Ｈｅｂｅｉ Ｕｎｉｖｅｒｓｉｔｙ， Ｂａｏｄｉｎｇ ０７１００２， Ｃｈｉｎａ； ４． Ｈｅｂｅｉ Ｂｒａｎｃｈ ｏｆ Ｍｅｔｅｏｒｏｌｏｇｉｃａｌ Ｃａｄｒｅｓ Ｔｒａｉｎｉｎｇ Ｉｎｓｔｉｔｕｔｅ， Ｃｈｉｎａ Ｍｅｔｅｏｒｏｌｏｇｉｃａｌ Ａｄｍｉｎｉｓｔｒａｔｉｏｎ， Ｂａｏｄｉｎｇ ０７１０００， Ｃｈｉｎａ） Ａｂｓｔｒａｃｔ：Ｆｅａｔｕｒｅ ｓｅｌｅｃｔｉｏｎ， ａｎ ｉｍｐｏｒｔａｎｔ ｓｔｅｐ ｉｎ ｄａｔａ ｍｉｎｉｎｇ， ｉｓ ａ ｐｒｏｃｅｓｓ ｔｈａｔ ｓｅｌｅｃｔｓ ａ ｓｕｂｓｅｔ ｆｒｏｍ ａｎ ｏｒｉｇｉｎａｌ ｆｅａｔｕｒｅ ｓｅｔ ｂａｓｅｄ ｏｎ ｓｏｍｅ ｃｒｉｔｅｒｉａ． Ｉｔｓ ｐｕｒｐｏｓｅ ｉｓ ｔｏ ｒｅｄｕｃｅ ｔｈｅ ｃｏｍｐｕｔａｔｉｏｎａｌ ｃｏｍｐｌｅｘｉｔｙ ｏｆ ｔｈｅ ｌｅａｒｎｉｎｇ ａｌｇｏｒｉｔｈｍ ａｎｄ ｔｏ ｉｍｐｒｏｖｅ ｔｈｅ ｐｅｒｆｏｒｍａｎｃｅ ｏｆ ｄａｔａ ｍｉｎｉｎｇ ｂｙ ｒｅｍｏｖｉｎｇ ｉｒｒｅｌｅｖａｎｔ ａｎｄ ｒｅｄｕｎｄａｎｔ ｆｅａｔｕｒｅｓ． Ｔｏ ｄｅａｌ ｗｉｔｈ ｔｈｅ ｐｒｏｂｌｅｍ ｏｆ ｄｉｓｃｒｅｔｅ ｖａｌｕｅｓ， ａ ｆｅａｔｕｒｅ ｓｅｌｅｃｔｉｏｎ ａｐｐｒｏａｃｈ ｗａｓ ｐｒｏｐｏｓｅｄ ｉｎ ｔｈｉｓ ｐａｐｅｒ． Ｉｔ ｕｓｅｓ ａ ｐａｒｔｉｃｌｅ ｓｗａｒｍ ｏｐｔｉｍｉｚａｔｉｏｎ ａｌｇｏｒｉｔｈｍ ｔｏ ｓｅａｒｃｈ ｔｈｅ ｏｐｔｉｍａｌ ｆｅａｔｕｒｅ ｓｕｂｓｅｔ． Ｆｕｒｔｈｅｒ， ｉｔ ｅｍｐｌｏｙｓ ｒｅｌａｔｉｖｅ ｃｌａｓｓｉｆｉｃａｔｉｏｎ ｉｎｆｏｒｍａｔｉｏｎ ｅｎｔｒｏｐｙ ａｓ ａ ｆｉｔｎｅｓｓ ｆｕｎｃｔｉｏｎ ｔｏ ｍｅａｓｕｒｅ ｔｈｅ ｓｉｇｎｉｆｉｃａｎｃｅ ｏｆ ｔｈｅ ｆｅａｔｕｒｅ ｓｕｂｓｅｔ． Ｔｈｅｎ， ｔｈｅ ｐｒｏｐｏｓｅｄ ａｐｐｒｏａｃｈ ｗａｓ ｃｏｍｐａｒｅｄ ｗｉｔｈ ｏｔｈｅｒ ｅｖｏｌｕｔｉｏｎａｒｙ ａｌｇｏｒｉｔｈｍ⁃ｂａｓｅｄ ｍｅｔｈｏｄｓ ｏｆ ｆｅａｔｕｒｅ ｓｅｌｅｃｔｉｏｎ． Ｔｈｅ ｅｘｐｅｒｉｍｅｎｔａｌ ｒｅｓｕｌｔｓ ｃｏｎｆｉｒｍ ｔｈａｔ ｔｈｅ ｐｒｏｐｏｓｅｄ ａｐｐｒｏａｃｈ ｏｕｔｐｅｒｆｏｒｍｓ ｇｅｎｅｔｉｃ ａｌｇｏｒｉｔｈｍ⁃ｂａｓｅｄ ｍｅｔｈｏｄｓ． Ｋｅｙｗｏｒｄｓ： ｄａｔａ ｍｉｎｉｎｇ； ｆｅａｔｕｒｅ ｓｅｌｅｃｔｉｏｎ； ｄａｔａ ｐｒｅｐｒｏｃｅｓｓｉｎｇ； ｒｏｕｇｈ ｓｅｔ； ｄｅｃｉｓｉｏｎ ｔａｂｌｅ； ｐａｒｔｉｃｌｅ ｓｗａｒｍ ｏｐｔｉｍｉｚａｔｉｏｎ； ｉｎｆｏｒｍａｔｉｏｎ ｅｎｔｒｏｐｙ； ｆｉｔｎｅｓｓ ｆｕｎｃｔｉｏｎ 收稿日期：２０１７－０５－０７． 网络出版日期：２０１７－０７－０３． 基金项目：国家自然科学基金项目（７１３７１０６３）； 河北省自然科学基金 项目（Ｆ２０１７２０１０２６）； 浙江省计算机科学与技术重中之重学 科（浙江师范大学）资助项目． 通信作者：翟俊海． Ｅ⁃ｍａｉｌ： ｍｃｚｊｈ＠ １２６．ｃｏｍ． 特征选择［１－２］ 是数据挖掘的重要预处理步骤， 通过删除不必要特征，以达到降低算法复杂度，提 高算法的性能。 特征子集的评价至关重要，特征子 集的评价准则或启发式确定后，特征选择问题从某 种意义上来说就是在特征空间中搜索最优特征子 集问题。 研究人员提出了许多特征选择算法，这些 算法有的是从设计特征子集搜索的方法考虑的，有 的是从设计评价特征子集重要性的度量考虑的。 特征选择方法主要有筛选法（ｆｉｌｔｅｒ ｍｅｔｈｏｄ ）、封

·398 智能系统学报 第12卷 装法(wrapper method)和嵌人法(embedded 算法的第一部专著Swarm Intelligence2)出版后，粒 method)3种分类。筛选法独立于学习算法，它依据 子群算法才得到广泛应用。为解决PS0算法在连 启发式（如依赖度、互信息、不一致性等）搜索整体 续空间中的局限性，Kennedy等]提出了离散二进 最优解。因为这类特征选择算法独立于数据挖掘 制PS0算法。在此基础上，Chuang等列提出了一 算法，所以通用性好，适应各种数据挖掘任务，研究 种改进的二进制粒子群算法(IBPSO),有效简化了 也最为广泛。实际上，粗糙集领域中的属性约简方 特征选择，并在医疗诊断基因表达领域取得了较好 法就是这类方法的一种典型代表[3-)。Swiniarski 的效果：Chuang等f3o基于Catfish机制，提出了一种 等)针对模式识别问题，系统地研究了特征选择的 二进制粒子群特征选择算法，可避免过早收敛的问 粗糙集方法；Jensen等[6)提出了基于模糊粗糙集的 题；Wang等[3]提出了一种基于粗糙集的粒子群算 方法，但是它在某些情况下不收敛：Bhatt等]针对 法，具有较强的搜索能力能更快地寻找到最优解； 文献[6]中的问题，深人研究模糊粗糙集特征选择 Cervante等]提出了基于信息嫡的BPSO方法，测 算法的收敛性，得出了非常有价值的结论：Jensen 试结果非常理想。Liu等〔)提出了一种集成邻域信 等[]研究了模糊粗糙集特征选择算法的可扩展性 息和粒子群算法的特征选择方法，结合粒子加权提 问题，并提出了相应的方法：钱宇华等)提出了基 高了算法的稳定性；Fog等面向高维和数据流 于粗糙集正域逼近的属性约简（或特征选择）加速 格式的大数据，提出了一种基于粒子群算法的特征 方法，该方法具有很高的计算效率，受到了广泛关 选择方法，提高测试精度的同时降低了处理 注：胡清华等[]在邻域粗糙集框架下研究了异构特 时间3)。 征选择问题，提出的特征选择算法可以处理实数值 本文选择相对分类信息熵作为适应度函数，用 异构特征选择问题。 粒子群算法搜索最优特征子集，并与其他进化算法 除了基于粗糙集知识的算法，其他特征选择问 进行了实验比较，实验结果表明本文所提的方法更 题代表性的工作还包括基于一致性的方法[2,1-2] 为有效。 基于互信息的方法[-]及基于依赖度的方 1 法等[16-7]。 基础知识 封装法以算法性能为标准衡量特征子集，由 1.1粒子群算法 Kohavi等于1997年提出[18]。多年来，一些专家学 粒子群算法是一种群体搜索行为。群体由若 者沿着封装法的思路做出了大量研究：Sindhwani等 千个粒子p:组成，P:包含位置信息x和速度信息 将多层感知器和SVM相结合，提出了基于最大输出 。位置信息x表示P:在第k次迭代时其位置信 信息的特征选择算法[19]：Yang等提出了一种随机 息，速度信息表示P:在第k次迭代时移动的速度 扰动特征选择方法，具有较好表示能力[20。封装法 和方向。从一组初始粒子（初始种群）出发，通过一 过于依赖学习算法，对于全部筛选出的特征子集， 次次迭代，不断更新速度和位置信息，每个粒子不 必须重复分类器训练的过程，虽然最终得到的特征 断向gbest和pbest靠近，最终找到整体最优解。方 子集比较理想，但复杂度太高，代价过大。 法过程如图1所示，具体步骤见第2节。 在嵌入法中，特征选择与分类器的构造同步完 粒子群算法应用的关键是问题编码和粒子适 成。实际上，著名的D3算法[2和CART算法[ 应度评价标准。在问题编码上，显然二进制编码是 都可以看作嵌入式特征选择方法。基于神经网络 最为合适的。在粒子适应度评价标准上，一个合适 剪枝思想，Setiono等[2]提出了一种特征选择算法。 的适应度函数对特征子集的选择影响很大，因此适 该算法通过计算删除某个特征（剪枝）对神经网络 应度函数的设计是尤为关键的。 性能的影响来选择特征。在此基础上，Shen等提出 1.2粗糙集 了基于SVM的敏感度特征选择算法2]。而后， 定义1设DT=(U,AUD,V,f月为知识涉及的 Perkins等提出了Grafting嵌人式特征选择算法[2]。 决策表。其中，U={x1,x2,…,xn}为论域；A={a1, 粒子群算法由Kennedy提出[2]，逐渐被专家学 a2,…,am}是描述对象的属性集合：D={d,即目标 者广泛接受和应用。但是直到2001年关于粒子群 概念唯一；V为属性值域；f:U×A→V为信息函数

装 法 （ ｗｒａｐｐｅｒ ｍｅｔｈｏｄ ） 和 嵌 入 法 （ ｅｍｂｅｄｄｅｄ ｍｅｔｈｏｄ）３ 种分类。 筛选法独立于学习算法，它依据 启发式（如依赖度、互信息、不一致性等） 搜索整体 最优解。 因为这类特征选择算法独立于数据挖掘 算法，所以通用性好，适应各种数据挖掘任务，研究 也最为广泛。 实际上，粗糙集领域中的属性约简方 法就是这类方法的一种典型代表［３－４］ 。 Ｓｗｉｎｉａｒｓｋｉ 等［５］针对模式识别问题，系统地研究了特征选择的 粗糙集方法；Ｊｅｎｓｅｎ 等［６］ 提出了基于模糊粗糙集的 方法，但是它在某些情况下不收敛；Ｂｈａｔｔ 等［７］ 针对 文献［６］中的问题，深入研究模糊粗糙集特征选择 算法的收敛性，得出了非常有价值的结论；Ｊｅｎｓｅｎ 等［８］研究了模糊粗糙集特征选择算法的可扩展性 问题，并提出了相应的方法；钱宇华等［９］ 提出了基 于粗糙集正域逼近的属性约简（或特征选择） 加速 方法，该方法具有很高的计算效率，受到了广泛关 注；胡清华等［１０］在邻域粗糙集框架下研究了异构特 征选择问题，提出的特征选择算法可以处理实数值 异构特征选择问题。 除了基于粗糙集知识的算法，其他特征选择问 题代表性的工作还包括基于一致性的方法［２，１１－１２］ 、 基于 互 信 息 的 方 法［１３－１５］ 及 基 于 依 赖 度 的 方 法等［１６－１７］ 。 封装法以算法性能为标准衡量特征子集，由 Ｋｏｈａｖｉ 等于 １９９７ 年提出［１８］ 。 多年来，一些专家学 者沿着封装法的思路做出了大量研究；Ｓｉｎｄｈｗａｎｉ 等 将多层感知器和 ＳＶＭ 相结合，提出了基于最大输出 信息的特征选择算法［１９］ ；Ｙａｎｇ 等提出了一种随机 扰动特征选择方法，具有较好表示能力［２０］ 。 封装法 过于依赖学习算法，对于全部筛选出的特征子集， 必须重复分类器训练的过程，虽然最终得到的特征 子集比较理想，但复杂度太高，代价过大。 在嵌入法中，特征选择与分类器的构造同步完 成。 实际上，著名的 ＩＤ３ 算法［２１］ 和 ＣＡＲＴ 算法［２２］ 都可以看作嵌入式特征选择方法。 基于神经网络 剪枝思想，Ｓｅｔｉｏｎｏ 等［２３］ 提出了一种特征选择算法。 该算法通过计算删除某个特征（剪枝）对神经网络 性能的影响来选择特征。 在此基础上，Ｓｈｅｎ 等提出 了基于 ＳＶＭ 的敏感度特征选择算法［２４］ 。 而后， Ｐｅｒｋｉｎｓ 等提出了 Ｇｒａｆｔｉｎｇ 嵌入式特征选择算法［２５］ 。 粒子群算法由 Ｋｅｎｎｅｄｙ 提出［２６］ ，逐渐被专家学 者广泛接受和应用。 但是直到 ２００１ 年关于粒子群 算法的第一部专著 Ｓｗａｒｍ Ｉｎｔｅｌｌｉｇｅｎｃｅ ［２７］ 出版后，粒 子群算法才得到广泛应用。 为解决 ＰＳＯ 算法在连 续空间中的局限性，Ｋｅｎｎｅｄｙ 等［２８］ 提出了离散二进 制 ＰＳＯ 算法。 在此基础上，Ｃｈｕａｎｇ 等［２９］ 提出了一 种改进的二进制粒子群算法（ ＩＢＰＳＯ），有效简化了 特征选择，并在医疗诊断基因表达领域取得了较好 的效果；Ｃｈｕａｎｇ 等［３０］基于 Ｃａｔｆｉｓｈ 机制，提出了一种 二进制粒子群特征选择算法，可避免过早收敛的问 题；Ｗａｎｇ 等［３１］ 提出了一种基于粗糙集的粒子群算 法，具有较强的搜索能力能更快地寻找到最优解； Ｃｅｒｖａｎｔｅ 等［３２］提出了基于信息熵的 ＢＰＳＯ 方法，测 试结果非常理想。 Ｌｉｕ 等［３３］提出了一种集成邻域信 息和粒子群算法的特征选择方法，结合粒子加权提 高了算法的稳定性；Ｆｏｎｇ 等［３４］ 面向高维和数据流 格式的大数据，提出了一种基于粒子群算法的特征 选择 方 法， 提 高 测 试 精 度 的 同 时 降 低 了 处 理 时间［３４］ 。 本文选择相对分类信息熵作为适应度函数，用 粒子群算法搜索最优特征子集，并与其他进化算法 进行了实验比较，实验结果表明本文所提的方法更 为有效。 １ 基础知识 １．１ 粒子群算法 粒子群算法是一种群体搜索行为。 群体由若 干个粒子 ｐｉ 组成，ｐｉ 包含位置信息 ｘ ｋ ｉ 和速度信息 ｖ ｋ ｉ 。 位置信息 ｘ ｋ ｉ 表示 ｐｉ 在第 ｋ 次迭代时其位置信 息，速度信息 ｖ ｋ ｉ 表示 ｐｉ 在第 ｋ 次迭代时移动的速度 和方向。 从一组初始粒子（初始种群）出发，通过一 次次迭代，不断更新速度和位置信息，每个粒子不 断向 ｇｂｅｓｔ 和 ｐｂｅｓｔ 靠近，最终找到整体最优解。 方 法过程如图 １ 所示，具体步骤见第 ２ 节。 粒子群算法应用的关键是问题编码和粒子适 应度评价标准。 在问题编码上，显然二进制编码是 最为合适的。 在粒子适应度评价标准上，一个合适 的适应度函数对特征子集的选择影响很大，因此适 应度函数的设计是尤为关键的。 １．２ 粗糙集 定义 １ 设 ＤＴ ＝ （Ｕ，Ａ∪Ｄ，Ｖ，ｆ）为知识涉及的 决策表。 其中，Ｕ ＝ ｛ ｘ１ ，ｘ２ ，…，ｘｎ ｝ 为论域；Ａ ＝ ｛ ａ１ ， ａ２ ，…，ａｍ ｝是描述对象的属性集合；Ｄ ＝ ｛ｄ｝，即目标 概念唯一；Ｖ 为属性值域； ｆ：Ｕ×Ａ→Ｖ 为信息函数。 ·３９８· 智 能 系 统 学 报 第 １２ 卷

第3期 翟俊海，等：基于粗糙集相对分类信息嫡和粒子群优化的特征选择方法 ·399. 开始 定理1给定决策表DT=(U,AUD,V,f),假 初始化粒子群 设A1,ACA且ACA2,则H(U/A2)≤H(U/A)。 定理1保证了本文提出的方法的收敛性，即能 计算每个粒子的适应度值 够以很高概率找到整体最优解。 更新pbest、gbest粒子位置和速度 算法1基于粒子群算法的特征选择算法。 输入离散值决策表DT=(U,AUD,V,f),群 是否满足 结束条件 体大小N、惯性系数W、常量系数c,和c,、数据集维 数D。 Y 输出结果○ 输出A'二A。 1)随机初始化大小为N的种群： 图1PS0算法流程图 Fig.I The flowchart of particle swarm optimization 2)repeat; algorithm 3)for(i=1;isN;i=i+1); 定义2对于任意条件属性子集BCA,B的等 4)用式(6)计算种群中每一个个体的适应 价关系为 度值； IND(B)={(x,y)∈U×UVb∈B, 5)更新历史最佳位置best: b(x)=b(y)} (1)》 6)end for; 式中b(x)和b(y)分别是对象x和y在属性b上的 7)更新全局最佳位置gbest; 属性值。 8)for(i=1;isN;i=i+1); 定义3令XCU,BCA,X关于B的下近似为 9)for(d=1;dsD;d=d+1); BX=x[x] (2)》 10)更新速度信息a 定义4令XCU,BCA,X关于B的上近似为 11)更新位置信息xa; 12)end for; BX={xl[x]B∩X≠} (3) 定义5令X二U,BCA,X关于B的边界域为 13)end for; 14)until(满足终止条件时)； BN(X)=BX-BX (4) 15)输出A'。 2基于粗糙集相对分类信息熵的粒子 本文选择适用于离散值特征选择的二进制粒 群特征选择方法 子群算法，问题的解可用d维0-1向量表示，其中d 是属性个数。向量的第i个分量为0或1表示属性 首先定义适用于特征选择问题的适应度函数。 是否被选择。特征选择的过程分为以下几步。 对于形如DT=(U,AUD,V,f)的决策表，BC 1)随机产生N。个0-1向量（粒子）作为初始粒 A,B和D对U的划分表示为 子群，其中N。是种群的大小。 U/B=X,+X2+…+Xm 2)利用式(6)计算所有粒子的适应度值。 U/D=Y,+Y2+…+Yk 3)更新粒子历史最优点pbest:将所有粒子的适应 定义6划分U/B相对于U/D的概率分布为 度值和其历史最佳点pbest做比对，择优更新pbest。 x n y P三X (5) 4)更新全局最最优点gbest:将所有粒子的适应 定义7划分U/B相对于U/D的相对分类信 度值和全局最优点gbest做比对，择优更新gbest。 息熵为 5)根据上一步更新得到的pbest和gbest,更新 粒子的速度和位置。其中速度是根据上一步得到 H(UWB)=-X TUPylogaPy (6) 的pbest和gbest按照公式(7)进行更新： 相对分类信息嫡反映的不一致程度与其值成 =wv c rand(pbest -x)+ 正比，因此值越小效果越好。本文所选择的适应度 czrand(gbest -x) (7) 函数，即(6)式定义的相对分类信息熵，可通过定理 这里需要注意的是，P:的位置信息x中的每个 1的证明来验证其合理性3]。 x只能取0或1，相应的速度信息也发生了改变，用

图 １ ＰＳＯ 算法流程图 Ｆｉｇ． １ Ｔｈｅ ｆｌｏｗｃｈａｒｔ ｏｆ ｐａｒｔｉｃｌｅ ｓｗａｒｍ ｏｐｔｉｍｉｚａｔｉｏｎ ａｌｇｏｒｉｔｈｍ 定义 ２ 对于任意条件属性子集 Ｂ⊆Ａ，Ｂ 的等 价关系为 ＩＮＤ（Ｂ） ＝ {（ｘ，ｙ） ∈ Ｕ × Ｕ ∀ｂ ∈ Ｂ， ｂ（ｘ） ＝ ｂ（ｙ）} （１） 式中 ｂ（ｘ）和 ｂ（ｙ）分别是对象 ｘ 和 ｙ 在属性 ｂ 上的 属性值。 定义 ３ 令 Ｘ⊆Ｕ，Ｂ⊆Ａ，Ｘ 关于 Ｂ 的下近似为 ＢＸ ＝ ｛ｘ ［ｘ］ Ｂ ⊆ Ｘ｝ （２） 定义 ４ 令 Ｘ⊆Ｕ，Ｂ⊆Ａ，Ｘ 关于 Ｂ 的上近似为 ＢＸ ＝ ｛ｘ ［ｘ］ Ｂ ∩ Ｘ ≠ ⌀｝ （３） 定义 ５ 令 Ｘ⊆Ｕ，Ｂ⊆Ａ，Ｘ 关于 Ｂ 的边界域为 ＢＮ（Ｘ） ＝ ＢＸ － ＢＸ （４） ２ 基于粗糙集相对分类信息熵的粒子 群特征选择方法 首先定义适用于特征选择问题的适应度函数。 对于形如 ＤＴ ＝ （Ｕ，Ａ∪Ｄ，Ｖ， ｆ ）的决策表，Ｂ⊆ Ａ，Ｂ 和 Ｄ 对 Ｕ 的划分表示为 Ｕ／ Ｂ ＝ Ｘ１ ＋ Ｘ２ ＋ … ＋ Ｘｍ Ｕ／ Ｄ ＝ Ｙ１ ＋ Ｙ２ ＋ … ＋ Ｙｋ 定义 ６ 划分 Ｕ／ Ｂ 相对于 Ｕ／ Ｄ 的概率分布为 ｐｉｊ ＝ Ｘｉ ∩ Ｙｊ Ｘｉ （５） 定义 ７ 划分 Ｕ／ Ｂ 相对于 Ｕ／ Ｄ 的相对分类信 息熵为 Ｈ（Ｕ／ Ｂ） ＝ － ∑ ｍ ｉ ＝ １ ∑ ｋ ｊ ＝ １ Ｘｉ Ｕ ｐｉｊ ｌｏｇ２ ｐｉｊ （６） 相对分类信息熵反映的不一致程度与其值成 正比，因此值越小效果越好。 本文所选择的适应度 函数，即（６）式定义的相对分类信息熵，可通过定理 １ 的证明来验证其合理性［３５］ 。 定理 １ 给定决策表 ＤＴ ＝ (Ｕ，Ａ∪Ｄ，Ｖ， ｆ ) ，假 设 Ａ１ ，Ａ２⊆Ａ 且 Ａ１⊆Ａ２ ，则 Ｈ（Ｕ／ Ａ２ ）≤Ｈ（Ｕ／ Ａ１ ）。 定理 １ 保证了本文提出的方法的收敛性，即能 够以很高概率找到整体最优解。 算法 １ 基于粒子群算法的特征选择算法。 输入 离散值决策表 ＤＴ ＝ （Ｕ，Ａ∪Ｄ，Ｖ，ｆ ），群 体大小 Ｎ、惯性系数 ｗ、常量系数 ｃ１ 和 ｃ２ 、数据集维 数 Ｄ。 输出 Ａ′⊆Ａ。 １）随机初始化大小为 Ｎ 的种群； ２）ｒｅｐｅａｔ； ３）ｆｏｒ（ｉ ＝ １；ｉ≤Ｎ；ｉ ＝ ｉ＋１） ； ４） 用式 （ ６） 计算种群中每一个个体的适应 度值； ５）更新历史最佳位置 ｂｅｓｔ； ６）ｅｎｄ ｆｏｒ； ７）更新全局最佳位置 ｇｂｅｓｔ； ８）ｆｏｒ（ｉ ＝ １；ｉ≤Ｎ；ｉ ＝ ｉ＋１） ； ９）ｆｏｒ（ｄ ＝ １；ｄ≤Ｄ；ｄ ＝ ｄ＋１）； １０）更新速度信息 ｖｉｄ ； １１）更新位置信息 ｘｉｄ ； １２）ｅｎｄ ｆｏｒ； １３）ｅｎｄ ｆｏｒ； １４）ｕｎｔｉｌ（满足终止条件时）； １５）输出 Ａ′。 本文选择适用于离散值特征选择的二进制粒 子群算法，问题的解可用 ｄ 维 ０－１ 向量表示，其中 ｄ 是属性个数。 向量的第 ｉ 个分量为 ０ 或 １ 表示属性 是否被选择。 特征选择的过程分为以下几步。 １）随机产生 Ｎ０ 个 ０－１ 向量（粒子）作为初始粒 子群，其中 Ｎ０ 是种群的大小。 ２）利用式（６）计算所有粒子的适应度值。 ３）更新粒子历史最优点 ｐｂｅｓｔ：将所有粒子的适应 度值和其历史最佳点 ｐｂｅｓｔ 做比对，择优更新 ｐｂｅｓｔ。 ４）更新全局最最优点 ｇｂｅｓｔ：将所有粒子的适应 度值和全局最优点 ｇｂｅｓｔ 做比对，择优更新 ｇｂｅｓｔ。 ５）根据上一步更新得到的 ｐｂｅｓｔ 和 ｇｂｅｓｔ，更新 粒子的速度和位置。 其中速度是根据上一步得到 的 ｐｂｅｓｔ 和 ｇｂｅｓｔ 按照公式（７）进行更新： ｖ ｋ＋１ ｉ ＝ ｗｖ ｋ ｉ ＋ ｃ１ ｒａｎｄ（ｐｂｅｓｔ － ｘ ｋ ｉ ） ＋ ｃ２ ｒａｎｄ（ｇｂｅｓｔ － ｘ ｋ ｉ ） （７） 这里需要注意的是，ｐｉ 的位置信息 ｘ ｋ ｉ 中的每个 ｘ ｋ ｉｄ只能取 ０ 或 １，相应的速度信息也发生了改变，用 第 ３ 期 翟俊海，等：基于粗糙集相对分类信息熵和粒子群优化的特征选择方法 ·３９９·

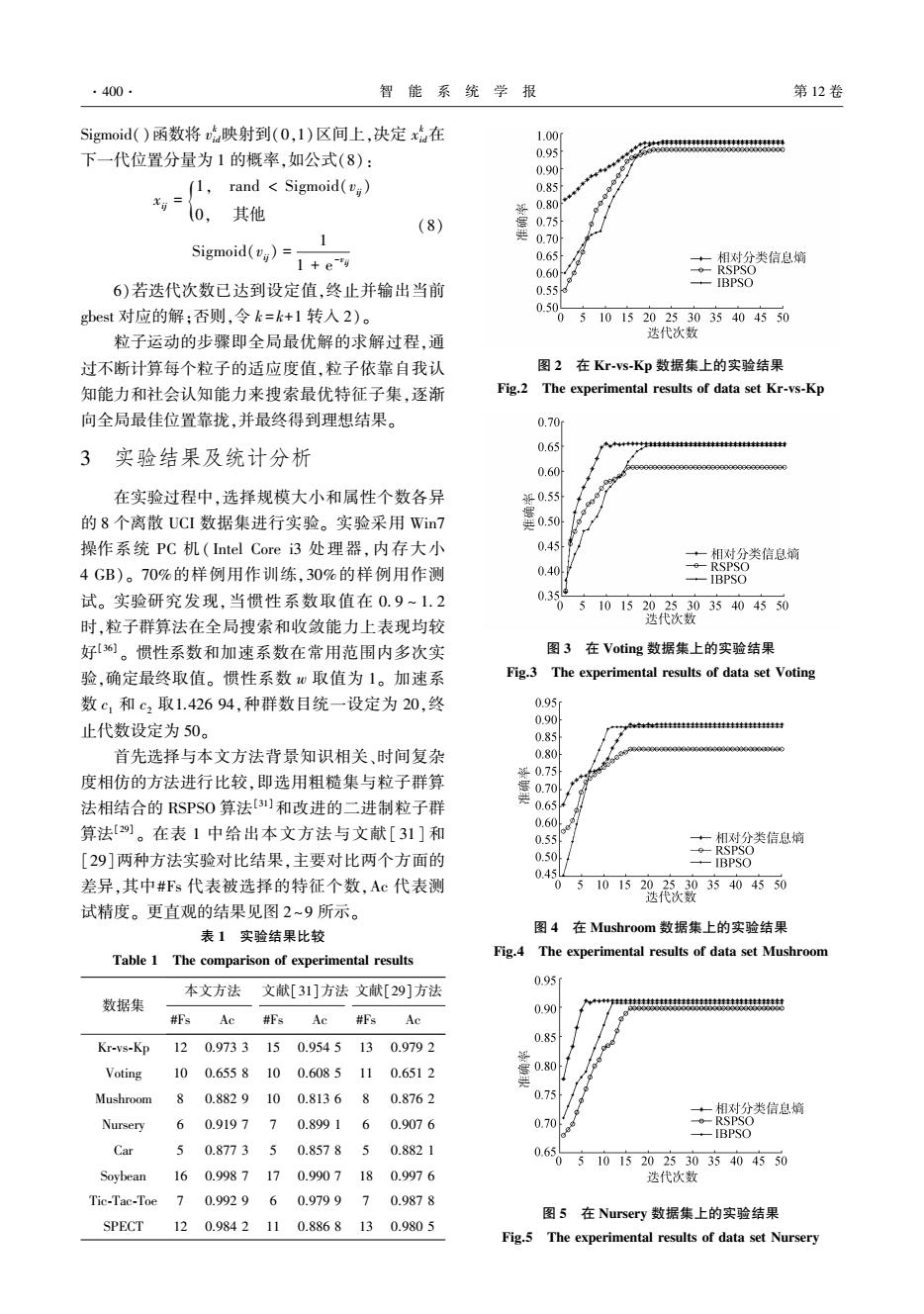
·400 智能系统学报 第12卷 Sigmoid()函数将v映射到(0,1)区间上，决定x在 1.00 5 下一代位置分量为1的概率，如公式(8)： 0.95 0.90 (1,rand Sigmoid(v;) 0.85 0,其他 解0.80 (8) 0.75 Sigmoid()=1 要0.70 1+e-y 0.65 +相对分类信息嫡 0.60 RSPSO 6)若迭代次数已达到设定值，终止并输出当前 IBPSO 0.55& gbest对应的解：否则，令k=k+1转入2)。 0.5 05101520253035404550 粒子运动的步骤即全局最优解的求解过程，通 迭代次数 过不断计算每个粒子的适应度值，粒子依靠自我认 图2在Kr-vs-Kp数据集上的实验结果 知能力和社会认知能力来搜索最优特征子集，逐渐 Fig.2 The experimental results of data set Kr-vs-Kp 向全局最佳位置靠拢，并最终得到理想结果。 0.70 0.65 *+4+4H4# 3实验结果及统计分析 0.60 在实验过程中，选择规模大小和属性个数各异 部0.55 的8个离散UCI数据集进行实验。实验采用Win7 操作系统PC机(Intel Core i3处理器，内存大小 0.45 ·相对分类信息镝 4GB)。70%的样例用作训练，30%的样例用作测 0.40 -e-RSPSO IBPSO 试。实验研究发现，当惯性系数取值在0.9~1.2 035 5 101520253035404550 时，粒子群算法在全局搜索和收敛能力上表现均较 迭代次数 好。惯性系数和加速系数在常用范围内多次实 图3在Voting数据集上的实验结果 验，确定最终取值。惯性系数心取值为1。加速系 Fig.3 The experimental results of data set Voting 数c1和c2取1.42694，种群数目统一设定为20，终 0.95m 0.90 止代数设定为50。 0.85 首先选择与本文方法背景知识相关、时间复杂 0.80 0.75 度相仿的方法进行比较，即选用粗糙集与粒子群算 0.70 法相结合的RSPS0算法[3)]和改进的二进制粒子群 0.654 0.60 算法[9。在表1中给出本文方法与文献[31]和 0.55 +一相对分类信息嫡 0.50 RSPSO [29]两种方法实验对比结果，主要对比两个方面的 -IBPSO 0.4 差异，其中#Fs代表被选择的特征个数，Ac代表测 0510152025.3035404550 迭代次数 试精度。更直观的结果见图2~9所示。 表1实验结果比较 图4在Mushroom数据集上的实验结果 Table 1 The comparison of experimental results Fig.4 The experimental results of data set Mushroom 0.95r 本文方法文献[31]方法文献[29]方法 数据集 0.90 思 #Fs Ac #Fs Ac #Fs Ac 0.85 Kr-vs-Kp 120.9733150.9545130.9792 Voting 100.6558100.6085110.6512 0.80 舞 Mushroom 8 0.8829100.81368 0.8762 0.75 一相对分类信息嫡 Nursery 60.919770.899160.9076 0.70 RSPSO ·-IBPSO Car 50.877350.85785 0.8821 0.6505101520253035404550 Soybean 160.9987170.9907180.9976 迭代次数 Tic-Tac-Toe70.992960.97997 0.9878 图5在Nursery数据集上的实验结果 SPECT120.984211 0.8868130.9805 Fig.5 The experimental results of data set Nursery

Ｓｉｇｍｏｉｄ（）函数将 ｖ ｋ ｉｄ映射到（０，１）区间上，决定 ｘ ｋ ｉｄ在 下一代位置分量为 １ 的概率，如公式（８）： ｘｉｊ ＝ １， ｒａｎｄ ＜ Ｓｉｇｍｏｉｄ（ｖｉｊ） {０， 其他 Ｓｉｇｍｏｉｄ（ｖｉｊ） ＝ １ １ ＋ ｅ －ｖｉｊ （８） ６）若迭代次数已达到设定值，终止并输出当前 ｇｂｅｓｔ 对应的解；否则，令 ｋ ＝ ｋ＋１ 转入 ２）。 粒子运动的步骤即全局最优解的求解过程，通 过不断计算每个粒子的适应度值，粒子依靠自我认 知能力和社会认知能力来搜索最优特征子集，逐渐 向全局最佳位置靠拢，并最终得到理想结果。 ３ 实验结果及统计分析 在实验过程中，选择规模大小和属性个数各异 的 ８ 个离散 ＵＣＩ 数据集进行实验。 实验采用 Ｗｉｎ７ 操作系统 ＰＣ 机（ Ｉｎｔｅｌ Ｃｏｒｅ ｉ３ 处理器，内存大小 ４ ＧＢ）。 ７０％的样例用作训练，３０％的样例用作测 试。 实验研究发现，当惯性系数取值在 ０􀆰 ９ ～ １􀆰 ２ 时，粒子群算法在全局搜索和收敛能力上表现均较 好［３６］ 。 惯性系数和加速系数在常用范围内多次实 验，确定最终取值。 惯性系数 ｗ 取值为 １。 加速系 数 ｃ１ 和 ｃ２ 取１．４２６ ９４，种群数目统一设定为 ２０，终 止代数设定为 ５０。 首先选择与本文方法背景知识相关、时间复杂 度相仿的方法进行比较，即选用粗糙集与粒子群算 法相结合的 ＲＳＰＳＯ 算法［３１］和改进的二进制粒子群 算法［２９］ 。 在表 １ 中给出本文方法与文献［ ３１］ 和 ［２９］两种方法实验对比结果，主要对比两个方面的 差异，其中＃Ｆｓ 代表被选择的特征个数，Ａｃ 代表测 试精度。 更直观的结果见图 ２～９ 所示。 表 １ 实验结果比较 Ｔａｂｌｅ １ Ｔｈｅ ｃｏｍｐａｒｉｓｏｎ ｏｆ ｅｘｐｅｒｉｍｅｎｔａｌ ｒｅｓｕｌｔｓ 数据集 本文方法 文献［３１］方法 文献［２９］方法 ＃Ｆｓ Ａｃ ＃Ｆｓ Ａｃ ＃Ｆｓ Ａｃ Ｋｒ⁃ｖｓ⁃Ｋｐ １２ ０．９７３ ３ １５ ０．９５４ ５ １３ ０．９７９ ２ Ｖｏｔｉｎｇ １０ ０．６５５ ８ １０ ０．６０８ ５ １１ ０．６５１ ２ Ｍｕｓｈｒｏｏｍ ８ ０．８８２ ９ １０ ０．８１３ ６ ８ ０．８７６ ２ Ｎｕｒｓｅｒｙ ６ ０．９１９ ７ ７ ０．８９９ １ ６ ０．９０７ ６ Ｃａｒ ５ ０．８７７ ３ ５ ０．８５７ ８ ５ ０．８８２ １ Ｓｏｙｂｅａｎ １６ ０．９９８ ７ １７ ０．９９０ ７ １８ ０．９９７ ６ Ｔｉｃ⁃Ｔａｃ⁃Ｔｏｅ ７ ０．９９２ ９ ６ ０．９７９ ９ ７ ０．９８７ ８ ＳＰＥＣＴ １２ ０．９８４ ２ １１ ０．８８６ ８ １３ ０．９８０ ５ 图 ２ 在 Ｋｒ⁃ｖｓ⁃Ｋｐ 数据集上的实验结果 Ｆｉｇ．２ Ｔｈｅ ｅｘｐｅｒｉｍｅｎｔａｌ ｒｅｓｕｌｔｓ ｏｆ ｄａｔａ ｓｅｔ Ｋｒ⁃ｖｓ⁃Ｋｐ 图 ３ 在 Ｖｏｔｉｎｇ 数据集上的实验结果 Ｆｉｇ．３ Ｔｈｅ ｅｘｐｅｒｉｍｅｎｔａｌ ｒｅｓｕｌｔｓ ｏｆ ｄａｔａ ｓｅｔ Ｖｏｔｉｎｇ 图 ４ 在 Ｍｕｓｈｒｏｏｍ 数据集上的实验结果 Ｆｉｇ．４ Ｔｈｅ ｅｘｐｅｒｉｍｅｎｔａｌ ｒｅｓｕｌｔｓ ｏｆ ｄａｔａ ｓｅｔ Ｍｕｓｈｒｏｏｍ 图 ５ 在 Ｎｕｒｓｅｒｙ 数据集上的实验结果 Ｆｉｇ．５ Ｔｈｅ ｅｘｐｅｒｉｍｅｎｔａｌ ｒｅｓｕｌｔｓ ｏｆ ｄａｔａ ｓｅｔ Ｎｕｒｓｅｒｙ ·４００· 智 能 系 统 学 报 第 １２ 卷

第3期 翟俊海，等：基于粗糙集相对分类信息嫡和粒子群优化的特征选择方法 ·401. 0.90 通过上述实验，我们可以看出采用相对分类信 0.80 息熵作适应度函数的粒子群算法与单纯粗糙集知 0.70 识作为适应度函数的粒子群算法相比，在实验精度 盖0a0 和筛选特征个数方面要明显占优。 接下来实验中，比较粒子群算法和遗传算法在 0.504 +相对分类信息嫡 处理特征选择上的优劣，对比方法为文献[35]中的 0.40 ◆-RSPSO -IBPSO 采用相同适应度函数的遗传特征选择方法。从#Fs、 0.3 05 101520253035404550 Ac、σ和Time4个方面进行了比较，结果列于表2 迭代次数 和表3中。其中，#Fs表示选出的特征数，Ac表示测 图6在Car数据集上的实验结果 试精度，c表示分类标准差，Time表示运行时间。 Fig.6 The experimental results of data set Car 更直观的实验结果如图10~17所示。 1.00 广88555288555555558555582港853 表2与遗传算法比较的实验结果(1) 0.95 Table 2 The experimental results compared with genetic algorithm(1) 0.90 本文方法 文献[35]方法 共0.85 数据集 #Fs Ac #Fs Ac 0.80 十相对分类信息嫡 RSPSO Kr-vs-Kp 12 0.9733 13 0.9516 ·-IBPSO 0.7505101520253035404550 Voting 10 0.6558 y 0.6224 迭代次数 Mushroom 8 0.8829 10 0.8371 图7在Sovbean数据集上的实验结果 Fig.7 The experimental results of data set Soybean Nursery 6 0.9197 > 0.9021 1.00 Car 5 0.8773 5 0.8628 0.99 0.98 Soybean 16 0.9987 9 0.9979 0.97 银0.96 Tic-Tac-Toe 7 0.9929 7 0.9935 0.95 共0.94 0.93 SPECT 12 0.9842 0.9769 0.92 +一相对分类信息嫡 --RSPSO 0.91 表3与遗传算法比较的实验结果(2) -IBPSO 0.9 5101520253035404550 Table 3 The experimental results compared with 0 迭代次数 genetic algorithm(2) 图8在Tic-Tac-Toe数据集上的实验结果 本文方法 文献[35]方法 数据集 Fig.8 The experimental results of data set Tic-Tac-Toe a Time a Time 1.00 Kr-vs-Kp 2.27×103415.25764.75×103508.5847 0.98 0.96 Voting 4.62×10324.31667.15×103 26.0479 0.94 Mushroom1.08×10-485.12186.68×10-3 96.0086 0.92 营0.90 0.88 Nursery 8.72×10-32311.14381.04×10-22653.8612 0.86 +相对分类信息熵 Car 5.19×10-3 10.52683.97×10-310.2885 0.84 --RSPSO 0.82 -IBPSO Sovbean2.01×10-335.17362.59×10-364.1101 0.8 05101520253035404550 迭代次数 Tic-Tac-Toe3.68×10-312.16356.02×10319.9828 图9在SPECT数据集上的实验结果 SPECT5.43×10-320.56397.52×10329.7611 Fig.9 The experimental results of data set SPECT

图 ６ 在 Ｃａｒ 数据集上的实验结果 Ｆｉｇ．６ Ｔｈｅ ｅｘｐｅｒｉｍｅｎｔａｌ ｒｅｓｕｌｔｓ ｏｆ ｄａｔａ ｓｅｔ Ｃａｒ 图 ７ 在 Ｓｏｙｂｅａｎ 数据集上的实验结果 Ｆｉｇ．７ Ｔｈｅ ｅｘｐｅｒｉｍｅｎｔａｌ ｒｅｓｕｌｔｓ ｏｆ ｄａｔａ ｓｅｔ Ｓｏｙｂｅａｎ 图 ８ 在 Ｔｉｃ⁃Ｔａｃ⁃Ｔｏｅ 数据集上的实验结果 Ｆｉｇ．８ Ｔｈｅ ｅｘｐｅｒｉｍｅｎｔａｌ ｒｅｓｕｌｔｓ ｏｆ ｄａｔａ ｓｅｔ Ｔｉｃ⁃Ｔａｃ⁃Ｔｏｅ 图 ９ 在 ＳＰＥＣＴ 数据集上的实验结果 Ｆｉｇ．９ Ｔｈｅ ｅｘｐｅｒｉｍｅｎｔａｌ ｒｅｓｕｌｔｓ ｏｆ ｄａｔａ ｓｅｔ ＳＰＥＣＴ 通过上述实验，我们可以看出采用相对分类信 息熵作适应度函数的粒子群算法与单纯粗糙集知 识作为适应度函数的粒子群算法相比，在实验精度 和筛选特征个数方面要明显占优。 接下来实验中，比较粒子群算法和遗传算法在 处理特征选择上的优劣，对比方法为文献［３５］中的 采用相同适应度函数的遗传特征选择方法。 从＃Ｆｓ、 Ａｃ、σ 和 Ｔｉｍｅ ４ 个方面进行了比较，结果列于表 ２ 和表 ３ 中。 其中，＃Ｆｓ 表示选出的特征数，Ａｃ 表示测 试精度，σ 表示分类标准差，Ｔｉｍｅ 表示运行时间。 更直观的实验结果如图 １０～１７ 所示。 表 ２ 与遗传算法比较的实验结果（１） Ｔａｂｌｅ ２ Ｔｈｅ ｅｘｐｅｒｉｍｅｎｔａｌ ｒｅｓｕｌｔｓ ｃｏｍｐａｒｅｄ ｗｉｔｈ ｇｅｎｅｔｉｃ ａｌｇｏｒｉｔｈｍ（１） 数据集 本文方法 文献［３５］方法 ＃Ｆｓ Ａｃ ＃Ｆｓ Ａｃ Ｋｒ⁃ｖｓ⁃Ｋｐ １２ ０．９７３ ３ １３ ０．９５１ ６ Ｖｏｔｉｎｇ １０ ０．６５５ ８ １２ ０．６２２ ４ Ｍｕｓｈｒｏｏｍ ８ ０．８８２ ９ １０ ０．８３７ １ Ｎｕｒｓｅｒｙ ６ ０．９１９ ７ ７ ０．９０２ １ Ｃａｒ ５ ０．８７７ ３ ５ ０．８６２ ８ Ｓｏｙｂｅａｎ １６ ０．９９８ ７ １９ ０．９９７ ９ Ｔｉｃ⁃Ｔａｃ⁃Ｔｏｅ ７ ０．９９２ ９ ７ ０．９９３ ５ ＳＰＥＣＴ １２ ０．９８４ ２ １５ ０．９７６ ９ 表 ３ 与遗传算法比较的实验结果（２） Ｔａｂｌｅ ３ Ｔｈｅ ｅｘｐｅｒｉｍｅｎｔａｌ ｒｅｓｕｌｔｓ ｃｏｍｐａｒｅｄ ｗｉｔｈ ｇｅｎｅｔｉｃ ａｌｇｏｒｉｔｈｍ（２） 数据集 本文方法 文献［３５］方法 σ Ｔｉｍｅ σ Ｔｉｍｅ Ｋｒ⁃ｖｓ⁃Ｋｐ ２．２７×１０ －３ ４１５．２５７ ６ ４．７５×１０ －３ ５０８．５８４ ７ Ｖｏｔｉｎｇ ４．６２×１０ －３ ２４．３１６ ６ ７．１５×１０ －３ ２６．０４７ ９ Ｍｕｓｈｒｏｏｍ １．０８×１０ －４ ８５．１２１ ８ ６．６８×１０ －３ ９６．００８ ６ Ｎｕｒｓｅｒｙ ８．７２×１０ －３ ２３１１．１４３ ８ １．０４×１０ －２ ２ ６５３．８６１ ２ Ｃａｒ ５．１９×１０ －３ １０．５２６ ８ ３．９７×１０ －３ １０．２８８ ５ Ｓｏｙｂｅａｎ ２．０１×１０ －３ ３５．１７３ ６ ２．５９×１０ －３ ６４．１１０ １ Ｔｉｃ⁃Ｔａｃ⁃Ｔｏｅ ３．６８×１０ －３ １２．１６３ ５ ６．０２×１０ －３ １９．９８２ ８ ＳＰＥＣＴ ５．４３×１０ －３ ２０．５６３ ９ ７．５２×１０ －３ ２９．７６１ １ 第 ３ 期 翟俊海，等：基于粗糙集相对分类信息熵和粒子群优化的特征选择方法 ·４０１·