
第12卷第5期 智能系统学报 Vol.12 No.5 2017年10月 CAAI Transactions on Intelligent Systems 0ct.2017 D0I:10.11992/is.201706014 网络出版地址:http:/kns.cmki.ne/kcms/detail/23.1538.TP.20170831.1058.006.html 一种精英反向学习的萤火虫优化算法 魏伟一,文雅宏 (西北师范大学计算机科学与工程学院,甘肃兰州730070) 摘要:为了提高传统莹火虫算法的收敛速度和求解精度,提出了一种精英反向学习的萤火虫优化算法。通过反向 学习策略构造精英群体,在精英群体构成的区间上求普通群体的反向解,增加了群体的多样性,提高了算法的收敛 速度:同时,为了避免最优个体陷入局部最优,使整个群体在搜索过程中出现停滞,提出了差分演化变异策略:最后, 提出了一种线性递减的自适应步长来平衡算法的开发能力。实验结果表明,算法在收敛速度和收敛精度上有更好 的效果。 关键词:萤火虫算法:精英反向学习:优化算法:精英群体:反向解:反向学习策略:差分演化变异:自适应步长 中图分类号:TP309.2文献标志码:A文章编号:1673-4785(2017)05-0710-07 中文引用格式:魏伟一,文雅宏.一种精英反向学习的萤火虫优化算法[J】.智能系统学报,2017,12(5):710-716, 英文引用格式:WEI Weiyi,WEN Yahong.Firefly optimization algorithm utilizing elite opposition-based learning[J].CAAI transactions on intelligent systems,2017,12(5):710-716. Firefly optimization algorithm utilizing elite opposition-based learning WEI Weiyi,WEN Yahong (College of Computer Science and Engineering,Northwest Normal University,Lanzhou 730070,China) Abstract:To increase the convergence speed and solution accuracy of the traditional firefly algorithm,in this paper,we propose a firefly optimization algorithm that utilizes elite opposition-based learning.Using an opposition- based learning strategy,we constructed an elite group and,in the interval of the elite group,we solved the opposite solutions of the ordinary groups.This strategy could increase group diversity and improve the convergence speed of the algorithm.To prevent the optimal individual from falling into the local optimum,which could cause stagnation of the whole group during the search process,we introduce a differential evolutionary mutation strategy.Finally,we propose an adaptive step size with a linear decrease to balance the development ability of the algorithm. Experimental results show that the proposed algorithm can increase convergence speed and accuracy. Keywords:firefly algorithm;elite opposition-based learning;optimized algorithm;elite group;opposite solutions; opposition-based learning strategy;differential evolutionary mutation;adaptive step size 萤火虫算法(firefly algorithm,FA)是受自然界问题的优化上,萤火虫算法依然存在收敛速度慢、 中萤火虫发光特性的启发,由剑桥学者Yang于 解的精度不高、容易陷入局部最优等不足。近年 2008年提出的一种群体智能随机优化算法[1-1。在来,很多学者已经进行了多角度的改进。文献[10] 多个科学与工程领域中,萤火虫算法已得到成功的 为了解决萤火虫算法过早地收敛和陷入局部最优 应用[6),虽然FA表现出了良好的性能,但在一些 的不足,利用广义反向学习策略来优化萤火虫算 法。文献[11]采用正交学习策略改进FA算法,利 收稿日期:2017-06-07.网络出版日期:2017-08-31. 基金项目:甘肃省科技计划资助项目(1506RZA130):甘肃省高等学校 用精英萤火虫来构造指导向量,通过指导向量引导 科研项目(2014B-018). 通信作者:文雅宏.E-mail:wwyahong@126.com. 群体向全局最优区域移动。文献「12]提出基于蛙
第 12 卷第 5 期 智 能 系 统 学 报 Vol.12 №.5 2017 年 10 月 CAAI Transactions on Intelligent Systems Oct. 2017 DOI:10.11992 / tis.201706014 网络出版地址:http: / / kns.cnki.net / kcms/ detail / 23.1538.TP.20170831.1058.006.html 一种精英反向学习的萤火虫优化算法 魏伟一,文雅宏 (西北师范大学 计算机科学与工程学院,甘肃 兰州 730070) 摘 要:为了提高传统萤火虫算法的收敛速度和求解精度,提出了一种精英反向学习的萤火虫优化算法。 通过反向 学习策略构造精英群体,在精英群体构成的区间上求普通群体的反向解,增加了群体的多样性,提高了算法的收敛 速度;同时,为了避免最优个体陷入局部最优,使整个群体在搜索过程中出现停滞,提出了差分演化变异策略;最后, 提出了一种线性递减的自适应步长来平衡算法的开发能力。 实验结果表明,算法在收敛速度和收敛精度上有更好 的效果。 关键词:萤火虫算法;精英反向学习;优化算法;精英群体;反向解;反向学习策略;差分演化变异;自适应步长 中图分类号:TP309.2 文献标志码:A 文章编号:1673-4785(2017)05-0710-07 中文引用格式:魏伟一,文雅宏.一种精英反向学习的萤火虫优化算法[J]. 智能系统学报, 2017, 12(5): 710-716. 英文引用 格 式: WEI Weiyi, WEN Yahong. Firefly optimization algorithm utilizing elite opposition⁃based learning [ J ]. CAAI transactions on intelligent systems, 2017, 12(5): 710-716. Firefly optimization algorithm utilizing elite opposition⁃based learning WEI Weiyi, WEN Yahong (College of Computer Science and Engineering, Northwest Normal University, Lanzhou 730070,China) Abstract:To increase the convergence speed and solution accuracy of the traditional firefly algorithm, in this paper, we propose a firefly optimization algorithm that utilizes elite opposition⁃based learning. Using an opposition⁃ based learning strategy, we constructed an elite group and, in the interval of the elite group, we solved the opposite solutions of the ordinary groups. This strategy could increase group diversity and improve the convergence speed of the algorithm. To prevent the optimal individual from falling into the local optimum, which could cause stagnation of the whole group during the search process, we introduce a differential evolutionary mutation strategy. Finally, we propose an adaptive step size with a linear decrease to balance the development ability of the algorithm. Experimental results show that the proposed algorithm can increase convergence speed and accuracy. Keywords:firefly algorithm; elite opposition⁃based learning; optimized algorithm; elite group; opposite solutions; opposition⁃based learning strategy; differential evolutionary mutation; adaptive step size 收稿日期:2017-06-07. 网络出版日期:2017-08-31. 基金项目:甘肃省科技计划资助项目(1506RJZA130);甘肃省高等学校 科研项目(2014B⁃018). 通信作者:文雅宏.E⁃mail:wwyahong@ 126.com. 萤火虫算法( firefly algorithm,FA) 是受自然界 中萤火虫发光特性的启发, 由剑桥学者 Yang 于 2008 年提出的一种群体智能随机优化算法[1-5] 。 在 多个科学与工程领域中,萤火虫算法已得到成功的 应用[6-9] ,虽然 FA 表现出了良好的性能,但在一些 问题的优化上,萤火虫算法依然存在收敛速度慢、 解的精度不高、容易陷入局部最优等不足。 近年 来,很多学者已经进行了多角度的改进。 文献[10] 为了解决萤火虫算法过早地收敛和陷入局部最优 的不足,利用广义反向学习策略来优化萤火虫算 法。 文献[11]采用正交学习策略改进 FA 算法,利 用精英萤火虫来构造指导向量,通过指导向量引导 群体向全局最优区域移动。 文献[12] 提出基于蛙

第5期 魏伟一,等:一种精英反向学习的萤火虫优化算法 ·711. 跳的萤火虫算法,在原始的FA算法中引入蛙跳算 有两个重要的影响因子,即亮度I和吸引度B。亮 法中的分群。同时,为了加强算法的局部开发能 度高说明其所处位置好,并吸引亮度低的个体向其 力,引入了模拟退火的思想。该算法对于高维多模 靠近。吸引度高则萤火虫移动的距离大。从FA开 态函数的优化问题,表现得还不够理想。文献[13] 始,萤火虫的个体随机地分布在指定的局域内,个 提出了一种基于多种群学习机制的萤火虫优化算 体的亮度由目标函数决定。 法,把萤火虫分为不同的子群,同时,子群建立学习 设1。表示萤火虫个体的固有亮度,Y为介质的 机制,实现不同子群间的信息交流,完成局部和全 光亮度吸收系数,「:为任意两个个体i和j的相对距 局的寻优。文献[14]引入模式搜索思想,把FA算 离(一般使用欧氏距离),B。为萤火虫个体固有吸引 法与模式搜索相结合,FA算法具有较强的全局搜索 度,随距离r变化的个体光强度1表示为 能力,模式搜索具有较好的局部搜索能力,利用两 I=loe-v2 (1) 者的优势来提高FA算法的性能。文献[15]针对高 则萤火虫i与萤火虫j之间的相互吸引力计算公 维问题,提出了多维反向学习的萤火虫算法,用反 式为 向学习策略初始化萤火虫种群。同时,用基于多维 B=B。×e-"g (2) 的方法更新不同维度上萤火虫的位置。算法在收 设x,(t)和x,(t)分别表示萤火虫i和j在t时刻 敛速度和精度上比原始萤火虫算法更优。 的位置,则两者之间的距离计算公式为 以上文献虽然对FA算法做了很好的改进,但 是在收敛速度和精度上还不够理想,为了更好地提 r=x(t)x(t)2 m)2 高FA算法的收敛速度和收敛精度,本文基于文献 (3) [16]利用精英反向学习策略来改进差分演化算法 萤火虫i向萤火虫移动,其位置更新方程为 的思想,提出了一种精英反向学习的萤火虫算法, 在文献[16]中,通过设置一个参数来选取精英个 多nu+)=x0+a0-0)+md-》 体,而本文根据原解和反向解适应度值的大小选取 (4) 精英个体,这样能更充分地利用精英群体的良好信 式中:x4(t+1)表示萤火虫i在t+1时刻的位置: 息,提高算法的收敛速度。同时,本文采用了差分 a∈[0,1],表示步长因子。 演化策略(differential evolutionary mutation)来增强 2精英反向学习的萤火虫算法 算法的局部搜索能力。最后,为了增强和平衡算法 的开发能力,本文提出了一种线性递减的自适应步 2.1 反向学习策略 长。在5个标准测试函数上进行实验,并和多个改 反向学习策略是近年来计算智能领域出现的 进的FA算法进行实验对比。结果表明,本文算法 新概念-],其主要思想是对一个问题的可行解, 在收敛速度和收敛精度上更好。 求其反向解,并对原解和反向解进行评估,从中选 出较优的解作为下一代个体。其中反向点和反向 1萤火虫算法(FA) 解的定义如下。 FA是受自然界中萤火虫个体通过发光来吸引 定义1反向点(opposite point,OP)[8)。设x= 同伴求偶或觅食行为的启发而提出的一种元启发 (x1,x2,…,xD)是D维空间中的一个点,且x1,x2,… 式算法[1-】,萤火虫之间相互吸引以及位置迭代更 xo∈R,x∈[a,b],则x对应的反向点x·=(x, 新的过程是搜索和优化的过程。寻找最亮萤火虫 x2,…,x0)定义为 的问题是求解最优值的问题,不断用最好的位置替 xi=ai+bi-x (5) 换较差的位置来完成整个搜索过程。在一定的搜 定义2动态反向学习策略(dynamic opposition 索区域内所有发光弱的萤火虫向发光强的萤火虫 based leaming,DOBL)。]i设x,(t)=((t),xa(t),…, 移动,从而实现位置寻优[]。每个萤火虫被看作一 xD(t))为问题第t代的一个可行解,x(t)是其j维 个个体,个体主要有“位置、亮度、吸引度”等属性, 上的分量,x(t)是x(t)对应的反向解,则x(t)是
跳的萤火虫算法,在原始的 FA 算法中引入蛙跳算 法中的分群。 同时,为了加强算法的局部开发能 力,引入了模拟退火的思想。 该算法对于高维多模 态函数的优化问题,表现得还不够理想。 文献[13] 提出了一种基于多种群学习机制的萤火虫优化算 法,把萤火虫分为不同的子群,同时,子群建立学习 机制,实现不同子群间的信息交流,完成局部和全 局的寻优。 文献[14]引入模式搜索思想,把 FA 算 法与模式搜索相结合,FA 算法具有较强的全局搜索 能力,模式搜索具有较好的局部搜索能力,利用两 者的优势来提高 FA 算法的性能。 文献[15]针对高 维问题,提出了多维反向学习的萤火虫算法,用反 向学习策略初始化萤火虫种群。 同时,用基于多维 的方法更新不同维度上萤火虫的位置。 算法在收 敛速度和精度上比原始萤火虫算法更优。 以上文献虽然对 FA 算法做了很好的改进,但 是在收敛速度和精度上还不够理想,为了更好地提 高 FA 算法的收敛速度和收敛精度,本文基于文献 [16]利用精英反向学习策略来改进差分演化算法 的思想,提出了一种精英反向学习的萤火虫算法, 在文献[16] 中,通过设置一个参数来选取精英个 体,而本文根据原解和反向解适应度值的大小选取 精英个体,这样能更充分地利用精英群体的良好信 息,提高算法的收敛速度。 同时,本文采用了差分 演化策略( differential evolutionary mutation) 来增强 算法的局部搜索能力。 最后,为了增强和平衡算法 的开发能力,本文提出了一种线性递减的自适应步 长。 在 5 个标准测试函数上进行实验,并和多个改 进的 FA 算法进行实验对比。 结果表明,本文算法 在收敛速度和收敛精度上更好。 1 萤火虫算法(FA) FA 是受自然界中萤火虫个体通过发光来吸引 同伴求偶或觅食行为的启发而提出的一种元启发 式算法[1-2] ,萤火虫之间相互吸引以及位置迭代更 新的过程是搜索和优化的过程。 寻找最亮萤火虫 的问题是求解最优值的问题,不断用最好的位置替 换较差的位置来完成整个搜索过程。 在一定的搜 索区域内所有发光弱的萤火虫向发光强的萤火虫 移动,从而实现位置寻优[17] 。 每个萤火虫被看作一 个个体,个体主要有“位置、亮度、吸引度” 等属性, 有两个重要的影响因子,即亮度 I 和吸引度 β。 亮 度高说明其所处位置好,并吸引亮度低的个体向其 靠近。 吸引度高则萤火虫移动的距离大。 从 FA 开 始,萤火虫的个体随机地分布在指定的局域内,个 体的亮度由目标函数决定。 设 I0 表示萤火虫个体的固有亮度,γ 为介质的 光亮度吸收系数,rij为任意两个个体 i 和 j 的相对距 离(一般使用欧氏距离),β0 为萤火虫个体固有吸引 度,随距离 r 变化的个体光强度 I 表示为 I = I0 e -γr 2 (1) 则萤火虫 i 与萤火虫 j 之间的相互吸引力计算公 式为 β = β0 × e -γr ij (2) 设 xi(t)和 xj(t)分别表示萤火虫 i 和 j 在 t 时刻 的位置,则两者之间的距离计算公式为 rij = ‖xi(t) - xj(t)‖2 = ∑ d m = 1 (xim - xjm ) 2 (3) 萤火虫 i 向萤火虫 j 移动,其位置更新方程为 xi+1 (t + 1) = xi (t) + β xj (t) - xi ( (t) ) + α rand - 1 2 æ è ç ö ø ÷ (4) 式中:xi+1( t+1) 表示萤火虫 i 在 t + 1 时刻的位置; α∈[0,1],表示步长因子。 2 精英反向学习的萤火虫算法 2.1 反向学习策略 反向学习策略是近年来计算智能领域出现的 新概念[18-19] ,其主要思想是对一个问题的可行解, 求其反向解,并对原解和反向解进行评估,从中选 出较优的解作为下一代个体。 其中反向点和反向 解的定义如下。 定义 1 反向点(opposite point,OP) [18] 。 设x= (x1,x2,…,xD )是 D 维空间中的一个点,且 x1,x2,…, xD∈R,xj∈[ aj,bj ],则 x 对应的反向点 x ∗ = ( x ∗ 1 , x ∗ 2 ,…,x ∗ D )定义为 x ∗ j = aj + bj - xj (5) 定义 2 动态反向学习策略(dynamic opposition based learning,DOBL)。 [18]设 xi(t)= (xi1(t),xi2(t),…, xiD(t))为问题第 t 代的一个可行解,xij( t)是其 j 维 上的分量,x ∗ ij (t)是 xij(t)对应的反向解,则 x ∗ i (t)是 第 5 期 魏伟一,等:一种精英反向学习的萤火虫优化算法 ·711·

·712· 智能系统学报 第12卷 x:(t)对应的反向解,其中 N(t))。[a(t),b(t)]为精英群体所构造的区间, xi(t)=k(a;(t)+b(t))-x(t) (6) 当反向解越过边界[a(t),b,(t)]时,可以用下列方 式中:a(t)=min(x,(t)),b(t)=max(x(t)为当前 式进行重置: 搜索区域的最小值和最大值,其随着迭代的改变, xi=a,(t),x写<a,(t) (8) 而发生变化;i∈[1,n]J∈[1,D];n是种群大小; xi=b(t),xi>b(t) D是解空间的维数:k是介于0~1的随机数。 2.3差分演化变异策略 2.2精英反向学习 在FA中,群体中的最优个体x✉引导群体向最 反向解的引入,可以扩大算法的搜索区域,但 优方向移动,如果x陷人局部最优,群体的移动终 对那些原解适应度值大于反向解适应度值的个体, 止,即收敛到局部最优,则群体无法到达全局最优。 对其进行反向区域的搜索,浪费时间,则应加强其 因此,本文为了求得全局最优解,引入差分变异策 领域搜索。而对原解适应度值小于反向解适应度 略,对x进行变异操作,使其陷入局部最优的概率 值的个体,对其进行反向区域的搜素价值要高于其 减小。 领域的开发价值。因此,本文将原解适应度值小于 本文要对最优个体进行变异操作,使其跳出局 反向解适应度值的个体作为研究对象,求其反向 部最优的概率增大,因此选择“DE/best/1”作为变 解,既可以扩大搜素区域,也能有效避免盲目搜索 异操作,公式为 带来的时间浪费。 Cg=xe,+F·(xn1J-xa2) (9) 同时,本文为了提高算法的收敛速度,首先在当前 式中:x,为最优个体的第j维;F是缩放系数;n1、 解所构造的空间中,求所有当前解的反向解:然后,通 n2是[1,n]上两个互不相同的随机整数,代表不同 过比较适应度值,选出那些原解适应度值大于反向解 个体的下标;j是维度:c是变异后的值。 适应度值的个体组成精英群体:最后,在精英群体构造 将变异后的个体和父代个体进行如下交叉 的新的搜索空间上,再求原解适应度值小于反向解适 操作: 应度值的个体的反向解。如果算法能收敛到全局最优 Ci' rand[0,1]≤CR或者j=rand(1,D) 解,则精英群体所形成的搜索区间必将收敛到最优解 .j' 其他 所在的区域,这样充分利用了精英群体的有效信息, (10) 在精英群体所构成的动态定义区间上生成反向解,引 式中:x为新生成个体的第j维;rand[0,1]是 导搜索向最优解靠近。 [0,1]的随机数:CR是交叉概率;rand(1,D)是[1, 定义3精英(elite)。设x,(t)=(xa,x2,…, D]的一个随机整数;参数F、CR分别设为1和0.1。 xD)是第1次迭代的一个解,其反向解为x(t), 2.4自适应步长 f(x)为目标函数。当f(x,(t)≥f八x:(t))时,称 在原始萤火虫算法FA中,步长因子α在每次 x,(t)为第t次迭代的精英个体,记为N,(t);当 迭代时保持不变。但是当α取较大的值时,增强了 f八x:(t))<f八x(t))时,称x,(t)为第t次迭代的普 算法的全局搜索能力,降低了算法的收敛速度和搜 索的精度:当α取较小的值时,有利于算法的局部 通个体,记为Q(t)。若精英群体的规模为p(1< p≤n,n为解的总个数)时,则p个精英个体可表示 搜索,提高了搜索精度和算法的收敛速度。在算法 为{N(t),N2(t),…,Nn(t)}C{x(t),x2(t),…, 迭代前期,较大的α有利于算法的全局搜索:在后 期,较小的α显得更有利。因此本文对α采用动态 x(t)}。 递减的方式,计算公式为 定义4精英反向解(elite opposite solution)i。 t 设x为普通个体x:在j维上的值,则其反向解可定 T- 10 义为 a,1=a·(T),t=1,2,…,T(11) xi(t)=k(a;(t)+b(t))-x(t) (7)》 式中t为迭代次数。 式中:k是介于0~l的随机数;a(t)=min(V,(t), 2.5E0FA算法描述 N2(t),…,N(t));b(t)=max(N(t),N2(t),…, EOFA算法流程如下
xi(t)对应的反向解,其中 x ∗ ij (t) = k(aj(t) + bj(t)) - xij(t) (6) 式中: a(t) = min(xij(t)),b(t) = max(xij(t)) 为当前 搜索区域的最小值和最大值,其随着迭代的改变, 而发生变化; i ∈ [1,n],j ∈ [1,D];n 是种群大小; D 是解空间的维数;k 是介于 0~1 的随机数。 2.2 精英反向学习 反向解的引入,可以扩大算法的搜索区域,但 对那些原解适应度值大于反向解适应度值的个体, 对其进行反向区域的搜索,浪费时间,则应加强其 领域搜索。 而对原解适应度值小于反向解适应度 值的个体,对其进行反向区域的搜素价值要高于其 领域的开发价值。 因此,本文将原解适应度值小于 反向解适应度值的个体作为研究对象,求其反向 解,既可以扩大搜素区域,也能有效避免盲目搜索 带来的时间浪费。 同时,本文为了提高算法的收敛速度,首先在当前 解所构造的空间中,求所有当前解的反向解;然后,通 过比较适应度值,选出那些原解适应度值大于反向解 适应度值的个体组成精英群体;最后,在精英群体构造 的新的搜索空间上,再求原解适应度值小于反向解适 应度值的个体的反向解。 如果算法能收敛到全局最优 解,则精英群体所形成的搜索区间必将收敛到最优解 所在的区域[16] ,这样充分利用了精英群体的有效信息, 在精英群体所构成的动态定义区间上生成反向解,引 导搜索向最优解靠近。 定义 3 精英( elite)。 设 xi(t) = (xi1 ,xi2 ,…, xiD) 是第 t 次迭代的一个解,其反向解为 x ∗ i (t), f(x) 为目标函数。 当 f(xi(t)) ≥ f(x ∗ i (t)) 时,称 xi(t) 为第 t 次迭代的精英个体, 记为 Ni(t) ; 当 f(xi(t)) < f(x ∗ i (t)) 时,称 xt(t) 为第 t 次迭代的普 通个体,记为 Qi(t)。 若精英群体的规模为 p(1 < p ≤n,n 为解的总个数) 时,则 p 个精英个体可表示 为 {N1(t),N2(t),…,Np(t)} ⊆ {x1(t),x2(t),…, xn(t)}。 定义 4 精英反向解(elite opposite solution) [18] 。 设 xij 为普通个体 xi 在 j 维上的值,则其反向解可定 义为 x ∗ ij (t) = k(aj(t) + bj(t)) - xij(t) (7) 式中:k 是介于 0 ~ 1 的随机数; aj(t) = min(N1j(t), N2j(t),…,Npj(t));bj(t) = max(N1j(t),N2j(t),…, Npj(t))。 [aj(t),bj(t)] 为精英群体所构造的区间, 当反向解越过边界 [aj(t),bj(t)] 时,可以用下列方 式进行重置: x ∗ ij = aj(t), x ∗ ij < aj(t) x ∗ ij = bj(t), x ∗ ij > bj(t) { (8) 2.3 差分演化变异策略 在 FA 中,群体中的最优个体 xbest引导群体向最 优方向移动,如果 xbest 陷入局部最优,群体的移动终 止,即收敛到局部最优,则群体无法到达全局最优。 因此,本文为了求得全局最优解,引入差分变异策 略,对 xbest 进行变异操作,使其陷入局部最优的概率 减小。 本文要对最优个体进行变异操作,使其跳出局 部最优的概率增大,因此选择“DE / best / 1” 作为变 异操作,公式为 cij = xbest, j + F· xn1 ,j - xn2 ,j ( ) (9) 式中: xbest,j 为最优个体的第 j 维; F 是缩放系数; n1 、 n2 是 [1,n] 上两个互不相同的随机整数,代表不同 个体的下标; j 是维度;cij是变异后的值。 将变异后的个体和父代个体进行如下交叉 操作: x - best, j = cij, rand[0,1] ≤ CR 或者 j = rand(1,D) xbest, j, 其他 { (10) 式中:x - best,j 为新生成个体的第 j 维; rand[0,1] 是 [0,1]的随机数;CR 是交叉概率;rand(1,D)是[1, D]的一个随机整数;参数 F、CR 分别设为 1 和 0.1。 2.4 自适应步长 在原始萤火虫算法 FA 中,步长因子 α 在每次 迭代时保持不变。 但是当 α 取较大的值时,增强了 算法的全局搜索能力,降低了算法的收敛速度和搜 索的精度;当 α 取较小的值时,有利于算法的局部 搜索,提高了搜索精度和算法的收敛速度。 在算法 迭代前期,较大的 α 有利于算法的全局搜索;在后 期,较小的 α 显得更有利。 因此本文对 α 采用动态 递减的方式,计算公式为 αt+1 = αt·( T - t 10 T ), t = 1,2,…,T (11) 式中 t 为迭代次数。 2.5 EOFA 算法描述 EOFA 算法流程如下。 ·712· 智 能 系 统 学 报 第 12 卷

第5期 魏伟一,等:一种精英反向学习的萤火虫优化算法 ·713· 输入目标函数和搜索空间: l)Sphere函数 输出全局最优解和最优位置。 1)初始化参数m,n,T,a,B,y,在[m,n]上生成 )=2.5e(-512,5.12 i=1 初始种群x,(i=1,2,…,n)。 Sphere函数为多维单峰值函数,在点x=(0,0,, 2)执行EOFA算法搜索。 0)处取得极小值0。 3)把x(t)(i=1,2,…,n)带入目标函数,计算 2)Rosenbrock函数 函数值,把目标函数的值作为每个个体的亮度 值1.(t)。 f=[100(,-》+(k-1)1. 4)在[m,n]生成x,(t)的反向解x,(t),并计算 x:∈(-2.048,2.048) 亮度I(t)。对I(t)和(t)进行比较,fI(t)>I Rosenbrock函数为多维病态二次函数,在点x= (t),则x,(t)为精英个体N(t),记精英群体大小为 (1,1,…,1)处取得全局极小值0。 p(p>1,i=1,2,…,p)。设精英个体的区间范围为 3)Ackley函数 [a(t),b(t)](若精英群体的规模小于2,则在x (t)(i=1,2,…,n)构成的区间上求x(i=1,2,…, -e点m+2.7128, f3(x)=-20e√名 n)的反向解)。elsex,(t)是普通个体,普通群体大小 x∈(-32.7,32.7) 为n-po Ackley函数为多维多峰值函数,在点x=(0,0,…, 5)用式(7)在精英个体构成的区间[a,(t),b,(t)] 0)处取得全局极小值0。 上计算普通群体的反向解x:'(t)(i=1,…,n-p)。 4)Griewank函数 6)精英群体和普通群体的反向解群体构成当 f(x)= os()+1, 前新种群,计算新种群的亮度,并进行排序,选出最 优的个体x(t)。 x:∈(-600,600) 7)用式(3)计算每个个体i和最优个体x(t) Griewank函数为多维多峰值函数,在点x=(0,0, 之间的距离R(t)。 …,0)处取得全局极小值0。 8)用式(2)计算吸引力B(t)。个体i向最优个 5)Rastrigin函数 体(t)移动,用公式(6)更新位置x“(t)。 9)用式(11)计算a(t),并用式(9)、(10)对最 f(x)=10d+ A-10e(2小, 优个体进行位置扰动。 x:∈(-5.12,5.12) 10)算法搜索结束,输出全局最优解和最优 Rastrigin函数为多维多峰值函数,在点x=(0,0,…, 位置。 0)处取得全局极小值0。 若种群的规模为n,空间维度为D,则种群初始 3.2EOFA算法的测试结果 化的时间复杂度为O(nD);从迭代开始到结束的整 实验环境为:Inter Core(TM)i5-2450MCPU@ 个过程中,迭代的次数为t,其中3)是计算种群的亮 2.50GHz,内存4GB,Window7操作系统,MATLAB 度,复杂度为O(nDt):4)~9)是建立新的种群,并进 7.8.0版本。分别选取标准的FA算法[),LFA算 行位置的更新,复杂度为O((6n-p)·D),p(p≤n) 法[20],MFA算法[2)与本文提出的E0FA算法在5 是精英群体的规模。因此本文算法的时间复杂度 为O(nDr)。 种标准的测试函数上进行实验比较,种群规模n取 40,初始a取值为0.98。维度D取10和30,y=1, 3实验仿真及分析 MFA算法中方向向量的个数m取30,其他参数分 3.1测试函数 别取T=1000,B=1。分别记录4种算法迭代1000 在仿真实验中,本文采用下列5个常用的标准 次并在测试函数上独立运行40次的最优值、最差值 测试函数对算法进行测试。 和平均值,结果如表1所示
输入 目标函数和搜索空间; 输出 全局最优解和最优位置 。 1)初始化参数 m,n,T,α,β,γ,在[m,n]上生成 初始种群 xi(i = 1,2,…,n)。 2)执行 EOFA 算法搜索。 3)把 xi(t) (i = 1,2,…,n)带入目标函数,计算 函数值, 把 目 标 函 数 的 值 作 为 每 个 个 体 的 亮 度 值Ii(t)。 4)在[m,n]生成 xi(t)的反向解 x ∗ i (t),并计算 亮度 I ∗ i (t)。 对 Ii(t)和 I ∗ i (t)进行比较,if Ii(t) >I ∗ i (t),则 xi(t)为精英个体 Ni(t),记精英群体大小为 p(p>1,i = 1,2,…,p)。 设精英个体的区间范围为 [aj(t),bj( t)] (若精英群体的规模小于 2,则在 xi (t)(i = 1,2,…,n)构成的区间上求 xi( i = 1,2,…, n)的反向解)。 elsexi(t)是普通个体,普通群体大小 为n-p。 5)用式(7)在精英个体构成的区间[aj(t),bj(t)] 上计算普通群体的反向解 xi ′(t)(i =1,…,n-p)。 6)精英群体和普通群体的反向解群体构成当 前新种群,计算新种群的亮度,并进行排序,选出最 优的个体 xbest(t) 。 7)用式(3)计算每个个体 i 和最优个体 xbest(t) 之间的距离 Rij(t) 。 8)用式(2)计算吸引力 βij(t)。 个体 i 向最优个 体 xbest(t) 移动,用公式(6)更新位置 x new i (t) 。 9)用式(11)计算 α( t),并用式(9)、(10)对最 优个体进行位置扰动。 10)算法搜索结束,输出全局最优解和最优 位置。 若种群的规模为 n,空间维度为 D,则种群初始 化的时间复杂度为 O(nD);从迭代开始到结束的整 个过程中,迭代的次数为 t,其中 3)是计算种群的亮 度,复杂度为 O(nDt);4) ~9)是建立新的种群,并进 行位置的更新,复杂度为 O((6n-p)·Dt),p(p≤n) 是精英群体的规模。 因此本文算法的时间复杂度 为 O(nDt)。 3 实验仿真及分析 3.1 测试函数 在仿真实验中,本文采用下列 5 个常用的标准 测试函数对算法进行测试。 1) Sphere 函数 f 1(x) = ∑ d i = 1 x 2 i , xi ∈ ( - 5.12,5.12) Sphere 函数为多维单峰值函数,在点 x = (0,0,…, 0)处取得极小值 0。 2) Rosenbrock 函数 f 2(x) = ∑ d-1 i = 1 [100 (xi+1 - x 2 i ) 2 + (xi - 1) 2 ], xi ∈ ( - 2.048,2.048) Rosenbrock 函数为多维病态二 次 函 数, 在 点 x = (1,1,…,1)处取得全局极小值 0。 3) Ackley 函数 f 3(x) = - 20e -0.2 1 d ∑ d i = 1 x 2 i - e 1 d ∑ d i = 1 cos(2πx i ) + 22.712 8, xi ∈ ( - 32.7,32.7) Ackley 函数为多维多峰值函数,在点 x = (0,0,…, 0)处取得全局极小值 0。 4) Griewank 函数 f 4(x) = ∑ d i = 1 x 2 i 4 000 - ∏ d i = 1 cos( x i i ) + 1, xi ∈ ( - 600,600) Griewank 函数为多维多峰值函数,在点 x = ( 0,0, …,0)处取得全局极小值 0。 5) Rastrigin 函数 f 5(x) = 10d + ∑ d i = 1 [x 2 i - 10cos(2πxi)], xi ∈ ( - 5.12,5.12) Rastrigin 函数为多维多峰值函数,在点 x = (0,0,…, 0)处取得全局极小值 0。 3.2 EOFA 算法的测试结果 实验环境为:Inter Core( TM) i5⁃2450M CPU@ 2.50 GHz,内存 4 GB,Window7 操作系统,MATLAB 7.8. 0 版本。 分别选取标准的 FA 算法[1] ,LFA 算 法[20] ,MFA 算法[21] 与本文提出的 EOFA 算法在 5 种标准的测试函数上进行实验比较,种群规模 n 取 40,初始 α 取值为 0.98。 维度 D 取 10 和 30,γ = 1, MFA 算法中方向向量的个数 m 取 30,其他参数分 别取T = 1 000,β = 1。 分别记录 4 种算法迭代 1 000 次并在测试函数上独立运行 40 次的最优值、最差值 和平均值,结果如表 1 所示。 第 5 期 魏伟一,等:一种精英反向学习的萤火虫优化算法 ·713·
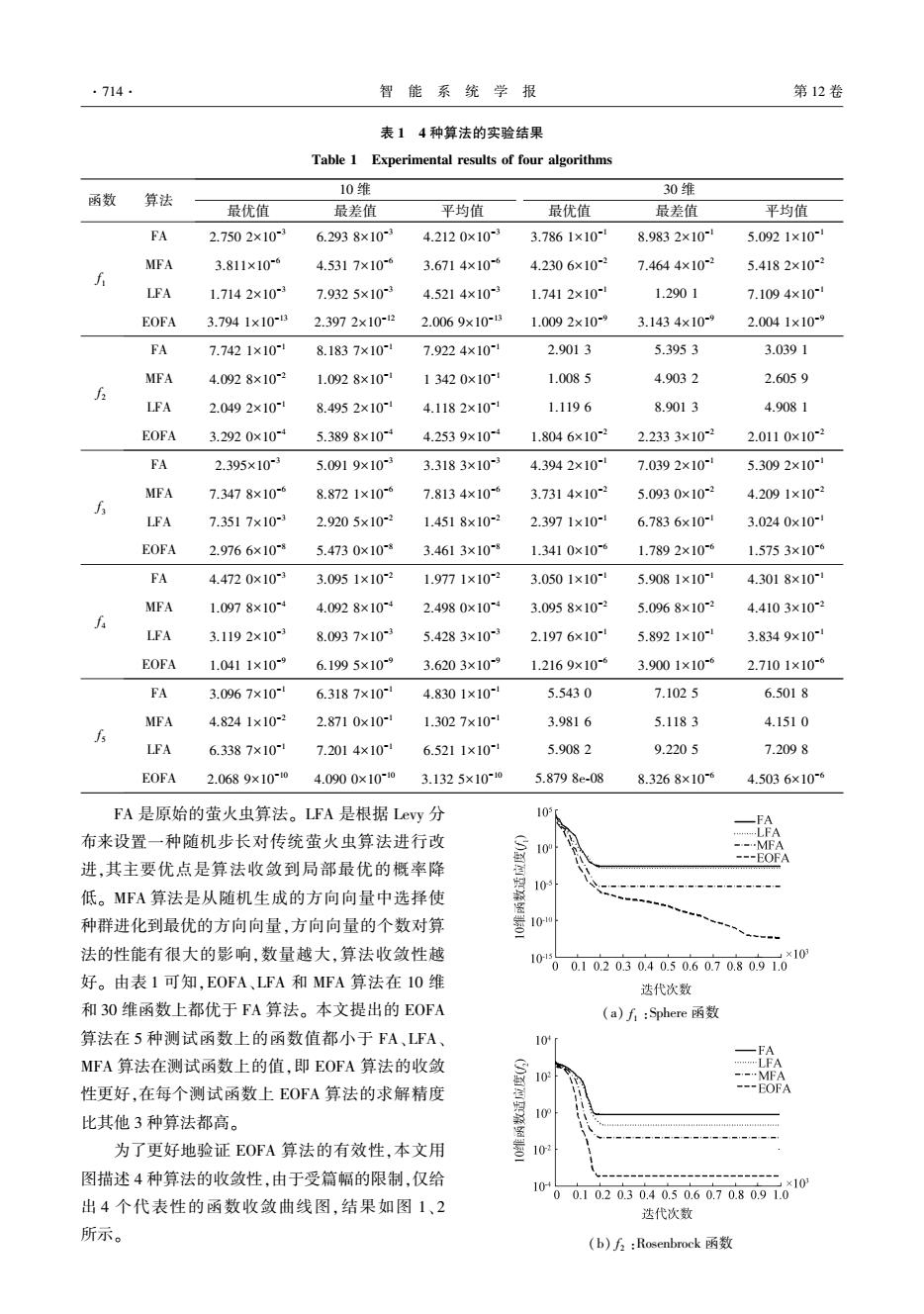
.714. 智能系统学报 第12卷 表14种算法的实验结果 Table 1 Experimental results of four algorithms 函数 10维 30维 算法 最优值 最差值 平均值 最优值 最差值 平均值 FA 2.7502×103 6.2938×103 4.2120×10 3.7861×10 8.9832×10 5.0921×10 MFA 3.811×10- 4.5317×10-6 3.6714×10-6 4.2306×102 7.4644×102 5.4182×102 LFA 1.7142×10-3 7.9325×10- 4.5214×103 1.7412×10- 1.2901 7.1094×10 EOFA 3.7941×108 2.3972×10-2 2.0069x10B 1.0092×10-9 3.1434×10-9 2.0041×10-9 FA 7.7421×10- 8.1837×10- 7.9224×10- 2.9013 5.3953 3.0391 MFA 4.0928×102 1.0928×10 13420×10 1.0085 4.9032 2.6059 LFA 2.0492×10- 8.4952×10 4.1182×10 1.1196 8.9013 4.9081 EOFA 3.2920×10-4 5.3898×104 4.2539×10 1.8046×10-2 2.2333×102 2.0110×102 FA 2.395×10- 5.0919×10- 3.3183×10- 4.3942×10- 7.0392×10 5.3092×10 MFA 7.3478×10-6 8.8721×10-6 7.8134×10-6 3.7314×10-2 5.0930×10-2 4.2091×102 LFA 7.3517×10- 2.9205×102 1.4518×102 2.3971×10-1 6.7836×10- 3.0240×10~1 EOFA 2.9766×10-8 5.4730×10 3.4613×10-8 1.3410×10-6 1.7892×10-6 1.5753×10-6 FA 4.4720×103 3.0951×102 1.9771×102 3.0501×10- 5.9081×10 4.3018×10 MFA 1.0978×10 4.0928×10+ 2.4980×10 3.0958×102 5.0968×10-2 4.4103×102 LFA 3.1192×10- 8.0937×10-3 5.4283×10- 2.1976×10 5.8921×10 3.8349×10 EOFA 1.0411×109 6.1995×10-9 3.6203×10-9 1.2169×10-6 3.9001×10-6 2.7101×10-6 FA 3.0967×10- 6.3187×101 4.8301×10 5.5430 7.1025 6.5018 MFA 4.8241×10-2 2.8710×10- 1.3027×10- 3.9816 5.1183 4.1510 LFA 6.3387×10- 7.2014×10 6.5211×10 5.9082 9.2205 7.2098 EOFA 2.0689×10-0 4.0900×10-10 3.1325×1010 5.8798e-08 8.3268×10-6 4.5036×10-6 FA是原始的萤火虫算法。LFA是根据Levy分 FA 布来设置一种随机步长对传统萤火虫算法进行改 LFA 10° -MFA --EOFA 进,其主要优点是算法收敛到局部最优的概率降 10 低。MFA算法是从随机生成的方向向量中选择使 种群进化到最优的方向向量,方向向量的个数对算 10W 法的性能有很大的影响,数量越大,算法收敛性越 10 ×10 00.10.20.30.40.50.60.70.80.91.0 好。由表1可知,EOFA、LFA和MFA算法在10维 迭代次数 和30维函数上都优于FA算法。本文提出的EOFA (a)f:Sphere函数 算法在5种测试函数上的函数值都小于FA、LFA、 10㎡ MFA算法在测试函数上的值,即EOFA算法的收敛 10 性更好,在每个测试函数上EOFA算法的求解精度 EOFA 10 比其他3种算法都高。 为了更好地验证EOFA算法的有效性,本文用 10 图描述4种算法的收敛性,由于受篇幅的限制,仅给 10 ×10 00.10.20.30.40.50.60.70.80.91.0 出4个代表性的函数收敛曲线图,结果如图1、2 迭代次数 所示。 (b)f5:Rosenbrock函数
表 1 4 种算法的实验结果 Table 1 Experimental results of four algorithms 函数 算法 10 维 30 维 最优值 最差值 平均值 最优值 最差值 平均值 f 1 FA 2.750 2×10 -3 6.293 8×10 -3 4.212 0×10 -3 3.786 1×10 -1 8.983 2×10 -1 5.092 1×10 -1 MFA 3.811×10 -6 4.531 7×10 -6 3.671 4×10 -6 4.230 6×10 -2 7.464 4×10 -2 5.418 2×10 -2 LFA 1.714 2×10 -3 7.932 5×10 -3 4.521 4×10 -3 1.741 2×10 -1 1.290 1 7.109 4×10 -1 EOFA 3.794 1×10 -13 2.397 2×10 -12 2.006 9×10 -13 1.009 2×10 -9 3.143 4×10 -9 2.004 1×10 -9 f 2 FA 7.742 1×10 -1 8.183 7×10 -1 7.922 4×10 -1 2.901 3 5.395 3 3.039 1 MFA 4.092 8×10 -2 1.092 8×10 -1 1 342 0×10 -1 1.008 5 4.903 2 2.605 9 LFA 2.049 2×10 -1 8.495 2×10 -1 4.118 2×10 -1 1.119 6 8.901 3 4.908 1 EOFA 3.292 0×10 -4 5.389 8×10 -4 4.253 9×10 -4 1.804 6×10 -2 2.233 3×10 -2 2.011 0×10 -2 f 3 FA 2.395×10 -3 5.091 9×10 -3 3.318 3×10 -3 4.394 2×10 -1 7.039 2×10 -1 5.309 2×10 -1 MFA 7.347 8×10 -6 8.872 1×10 -6 7.813 4×10 -6 3.731 4×10 -2 5.093 0×10 -2 4.209 1×10 -2 LFA 7.351 7×10 -3 2.920 5×10 -2 1.451 8×10 -2 2.397 1×10 -1 6.783 6×10 -1 3.024 0×10 -1 EOFA 2.976 6×10 -8 5.473 0×10 -8 3.461 3×10 -8 1.341 0×10 -6 1.789 2×10 -6 1.575 3×10 -6 f 4 FA 4.472 0×10 -3 3.095 1×10 -2 1.977 1×10 -2 3.050 1×10 -1 5.908 1×10 -1 4.301 8×10 -1 MFA 1.097 8×10 -4 4.092 8×10 -4 2.498 0×10 -4 3.095 8×10 -2 5.096 8×10 -2 4.410 3×10 -2 LFA 3.119 2×10 -3 8.093 7×10 -3 5.428 3×10 -3 2.197 6×10 -1 5.892 1×10 -1 3.834 9×10 -1 EOFA 1.041 1×10 -9 6.199 5×10 -9 3.620 3×10 -9 1.216 9×10 -6 3.900 1×10 -6 2.710 1×10 -6 f 5 FA 3.096 7×10 -1 6.318 7×10 -1 4.830 1×10 -1 5.543 0 7.102 5 6.501 8 MFA 4.824 1×10 -2 2.871 0×10 -1 1.302 7×10 -1 3.981 6 5.118 3 4.151 0 LFA 6.338 7×10 -1 7.201 4×10 -1 6.521 1×10 -1 5.908 2 9.220 5 7.209 8 EOFA 2.068 9×10 -10 4.090 0×10 -10 3.132 5×10 -10 5.879 8e⁃08 8.326 8×10 -6 4.503 6×10 -6 FA 是原始的萤火虫算法。 LFA 是根据 Levy 分 布来设置一种随机步长对传统萤火虫算法进行改 进,其主要优点是算法收敛到局部最优的概率降 低。 MFA 算法是从随机生成的方向向量中选择使 种群进化到最优的方向向量,方向向量的个数对算 法的性能有很大的影响,数量越大,算法收敛性越 好。 由表 1 可知,EOFA、LFA 和 MFA 算法在 10 维 和 30 维函数上都优于 FA 算法。 本文提出的 EOFA 算法在 5 种测试函数上的函数值都小于 FA、LFA、 MFA 算法在测试函数上的值,即 EOFA 算法的收敛 性更好,在每个测试函数上 EOFA 算法的求解精度 比其他 3 种算法都高。 为了更好地验证 EOFA 算法的有效性,本文用 图描述 4 种算法的收敛性,由于受篇幅的限制,仅给 出 4 个代表性的函数收敛曲线图,结果如图 1、2 所示。 (a) f 1 :Sphere 函数 (b) f 2 :Rosenbrock 函数 ·714· 智 能 系 统 学 报 第 12 卷