
第12卷第3期 智能系统学报 Vol.12 No.3 2017年6月 CAAI Transactions on Intelligent Systems Jun.2017 D0I:10.11992/is.201704022 网络出版地址:http:/kns.cmki.net/kcms/detail/23.1538.TP.20170s08.0922.010.html 利用二元拟阵K.图的一种建格方法 毛华,史明 (河北大学数学与信息科学学院,河北保定,071002)】 摘要:由于交通网络纷繁复杂,难以直观分析和直接处理。若出行者根据自己喜好和习惯决定出行策略,则需对 出行方案有清楚的了解。针对此问题,建立交通网络图一K模型,对具有带环路和重边路的复杂网络结构图,可 以完全转化为K图处理。通过概,念格理论,得到Hsse示图,方便人们对某些属性条件方案的提取,便于后续工作 处理。对K图进行研究之后发现,在特定的多个属性影响下,会形成一个三角形圈,于是结合拟阵中二元拟阵的标 准矩阵的定义,挖掘出一种特殊形式背景。根据这种形式背景的特殊性,给出基于二元拟阵的K图的概念格算法。 结合生活中的例子,验证该算法可行性。由于模型具有这种普遍性,所有结果可推广到具有类似形式背景的其他领 域研究中。 关键词:二元拟阵;标准矩阵表示;K图;二部图;图论;概念格;形式背景;Hsse示图 中图分类号:TP18文献标志码:A文章编号:1673-4785(2017)03-0333-08 中文引用格式:毛华,史明.利用二元拟阵K图的一种建格方法[J].智能系统学报,2017,12(3):333-340. 英文引用格式:MAO Hua,SHI Ming.A constructive method of lattice using the K。diagram of binary matroid[J].CAAI transactions on intelligent systems,2017,12(3):333-340. A constructive method of lattice using the K,diagram of binary matroid MAO Hua,SHI Ming School of Mathematics and Information Science,Hebei University,Baoding 071002,China) Abstract:Because of the complexity of traffic networks,it is difficult to directly analyze and deal with them.If some travelers wish to determine their travel strategy based on their preferences and habits,they should have a clear understanding of their travel plan.To address this problem,a traffic network,K model,was established in this study.It was used to elucidate how to transfer complex networks comprising loops or multiple edges to the K. diagram.With the assistance of formal concept analysis,the corresponding Hasse diagram of the K model was provided.The Hasse diagram facilitates travelers to extract some attributes under certain preconditions,after which the travelers can easily continue their work.Hence,the study of the K.diagram revealed that a triangle circle would form under some effects of specific multiple attributes.Thus,combining with the standard definition of the matrix for binary matroids,a special formal context was obtained.According to the particularity of the formal context,an algorithm was proposed based on the binary matroids for the K diagram.Utilizing an example,the feasibility of the proposed method was proven.Because the model is universal,the discussions of this research can be extended to other fields with similar formal context. Keywords:binary matroid;standard matrix representative;K.diagram;bipartite graph;graph theory;concept lattice:formal context:Hasse diagram 现代经济发展中,大城市经济圈)]内至少有一 式现已成为城市经济圈发展的增长级。实践证明, 个或多个经济发达并具有较强城市功能的中心城 经济圈中以三个地区为最好,例如京津冀经济圈、 市,以便带动周围其他城市的发展,这种经济圈模 长江三角洲经济圈、珠三角经济圈等。另外,从数 学方面分析,若将经济圈中每个城市视为一个顶 收稿日期:2017-04-19.网络出版日期:2017-05-08. 点,城市间有路可达时连接为边,则一个经济圈为 基金项目:国家自然科学基金项目(61572011). 一个图。依据图论的知识可知,在多边形图中,三 通信作者:史明.E-mail:ming1254610676@163.com
第 12 卷第 3 期 智 能 系 统 学 报 Vol.12 №.3 2017 年 6 月 CAAI Transactions on Intelligent Systems Jun. 2017 DOI:10.11992 / tis. 201704022 网络出版地址:http: / / kns.cnki.net / kcms/ detail / 23.1538.TP.20170508.0922.010.html 利用二元拟阵 K n 图的一种建格方法 毛华,史明 (河北大学 数学与信息科学学院,河北 保定, 071002) 摘 要:由于交通网络纷繁复杂,难以直观分析和直接处理。 若出行者根据自己喜好和习惯决定出行策略,则需对 出行方案有清楚的了解。 针对此问题,建立交通网络图———Kn模型,对具有带环路和重边路的复杂网络结构图,可 以完全转化为 Kn图处理。 通过概念格理论,得到 Hasse 示图,方便人们对某些属性条件方案的提取,便于后续工作 处理。 对 Kn图进行研究之后发现,在特定的多个属性影响下,会形成一个三角形圈,于是结合拟阵中二元拟阵的标 准矩阵的定义,挖掘出一种特殊形式背景。 根据这种形式背景的特殊性,给出基于二元拟阵的 Kn图的概念格算法。 结合生活中的例子,验证该算法可行性。 由于模型具有这种普遍性,所有结果可推广到具有类似形式背景的其他领 域研究中。 关键词:二元拟阵;标准矩阵表示;Kn图;二部图;图论;概念格;形式背景;Hasse 示图 中图分类号:TP18 文献标志码:A 文章编号:1673-4785(2017)03-0333-08 中文引用格式:毛华,史明.利用二元拟阵 Kn 图的一种建格方法[J]. 智能系统学报, 2017, 12(3): 333-340. 英文引用格式: MAO Hua, SHI Ming. A constructive method of lattice using the Kn diagram of binary matroid [ J]. CAAI transactions on intelligent systems, 2017, 12(3): 333-340. A constructive method of lattice using the Kn diagram of binary matroid MAO Hua, SHI Ming (School of Mathematics and Information Science, Hebei University, Baoding 071002, China) Abstract:Because of the complexity of traffic networks, it is difficult to directly analyze and deal with them. If some travelers wish to determine their travel strategy based on their preferences and habits, they should have a clear understanding of their travel plan. To address this problem, a traffic network, Kn model, was established in this study. It was used to elucidate how to transfer complex networks comprising loops or multiple edges to the Kn diagram. With the assistance of formal concept analysis, the corresponding Hasse diagram of the Kn model was provided. The Hasse diagram facilitates travelers to extract some attributes under certain preconditions, after which the travelers can easily continue their work. Hence, the study of the Kn diagram revealed that a triangle circle would form under some effects of specific multiple attributes. Thus, combining with the standard definition of the matrix for binary matroids, a special formal context was obtained. According to the particularity of the formal context, an algorithm was proposed based on the binary matroids for the Kn diagram. Utilizing an example, the feasibility of the proposed method was proven. Because the model is universal, the discussions of this research can be extended to other fields with similar formal context. Keywords: binary matroid; standard matrix representative; Kn diagram; bipartite graph; graph theory; concept lattice; formal context; Hasse diagram 收稿日期:2017-04-19. 网络出版日期:2017-05-08. 基金项目:国家自然科学基金项目(61572011). 通信作者:史明. E⁃mail:ming1254610676@ 163.com. 现代经济发展中,大城市经济圈[1] 内至少有一 个或多个经济发达并具有较强城市功能的中心城 市,以便带动周围其他城市的发展,这种经济圈模 式现已成为城市经济圈发展的增长级。 实践证明, 经济圈中以三个地区为最好,例如京津冀经济圈、 长江三角洲经济圈、珠三角经济圈等。 另外,从数 学方面分析,若将经济圈中每个城市视为一个顶 点,城市间有路可达时连接为边,则一个经济圈为 一个图。 依据图论的知识可知,在多边形图中,三

·334 智能系统学报 第12卷 个顶点构成的圈(即三角形)是最稳定的,因此本文 [L,D]是M在模2域上的一个标准矩阵表示,其中 考虑的圈将以三角形为基本单元。 p(b)是I中第i列,而p(e)是D中的第j列,1≤ 随着经济的发展,许多城市面临着严重的交通 i≤r,1≤j≤qo 拥堵。若出行者对自己要经过交通网络的路径、费 引理14 在一个具有n个顶点的无向完全图 用、时间等能够以清晰地、直观地方式得到,则完成 任务的效率将会大大提高。关于在复杂的交通网 中,包含的边数为(n-1) 络的条件下,研究合理的出行路径模型和算法,请 定义4)]形式背景K=(G,M,)定义为一个 参见文献[2-9]。基于多属性条件路径选择问题, 三元数组,其中G中的元素被称为对象,M中的元 文献[2-9]以及目前掌握的材料中,均没有涉及对 素被称为属性。IGxM,用glm表示(g,m)∈I,即 于交通网路信息提取的概念格[1]可视化研究。 对象g具有属性m。 概念格建立了对象和属性之间的一种概念层 定义5)形式背景(G,M,I)中的概念定义为 次结构,是数据分析和规则提取的一种有效工具。 元素对(A,B),其中A二G,BCM,A称为概念的外 Whitney!在1935年首次提出的拟阵已经被广泛 延,B称为概念的内涵,并且满足以下条件: 地应用于信息编码[]和网络安全[]等领域。将拟 1)B'={a∈GHb∈B,alb},A'={b∈M|Ha∈ 阵与概念格理论结合、图论[4]与概念格理论结合 来解决问题,已有许多成功的案例[6-2) A,alb 2)ACA",BCB"; 由于现实生活中,人们出行受多个属性条件的 限制,针对这些限制,经过研究发现K。简单图中形 3)(A)'=04,(9B,)'=0B'。 成三角形圈的一种特殊性质。由此,可以对复杂的 定义6设(A1,B,)、(A2,B2)是L(G,M,I) 交通网络进行分析、转化,形成K简单图。进而,能 中的两个概念,定义二元关系(A1,B,)≤(A2,B2)台 够建立网络模型,构建模型所对应的关联矩阵。依 ACA2台B,CB2,称(A1,B,)是(A2,B2)的子概念, 据K,图所产生的特殊形式背景,建立概念格信息提 (A2,B2)是(A1,B,)的父概念。若不存在概念(A3, 取方法。从而,给出基于二元拟阵K图的一种建格 B3)使得(A1,B1)≤(A3,B3)≤(A2,B2)成立,则称 方法,并利用具体实例验证方法的正确性与有效性。 (A1,B)是(A2,B2)的直接子概念,(A2,B2)是(A1, 1 预备知识 B,)的直接父概念。 不难证明这种父概念一子概念关系(也称泛 本节主要介绍网络K图、拟阵和概念格一些定 化-特化关系)是L(G,M,I)上的一个偏序关系。事 义与相关结论。有关图的基本概念和完全图的定 实上L(G,M,)关于该偏序关系是一个完备格,称 义,读者请参见文献[14]。有关二元拟阵和图的拟 为形式背景(G,M,I)的概念格,记为L(G,M,I)。 阵可表示性请参见文献[11]。 引理2]设(G,M,)是一个形式背景,则 定义1设任意(无向)图G=(V,E),其中 L(G,M,)关于上面定义的序“≤”构成的是完备 顶点集V={u1,2,…,vn},边集E={e1,e2,…,e.}。 格,其中上下确界由下式给出: 用m表示顶点:与边e,关联的次数,可能取值为 0,1,2,称所得矩阵M(G)=(m:)x.为图G的关联 V(4,B)=(A)”,0B) 矩阵。 Λje(4,B)=(∩A,(UB)") 定义24V(G)=XUY,X∩Y=⑦,X中任二 为了模型的建立和讨论表述简捷,给出如下几 项不相邻,Y中任二项不相邻,则G为二部图;若X 个定义。 中每个顶点皆与Y中一切顶点相邻,则G为完全二 定义7含圈基:在K图中满足从一个顶点出 部图,记Km,a,其中m=|x|,n=|Y|。 发,到其他n-1个顶点的相连接的边叫做含圈基。 定义3)设M是关于E={b1,b2,…,b,e1, 定义8基顶点:在K,图中满足从一个顶点出 e2,…,e,}的一个拟阵,其中B=b1,b2,…,b,}是M 发包含的所有相连的含圈基的顶点叫做基顶点。 的一个基。设C,是BU{e,}所含的基本圈,定义r× 定义9基最小圈:在一个三角形最小圈中,满 足一个最小圈中包含两个基的三角形圈,叫做基最 q阶矩阵D=(dg),其中d,= ,若b,∈C,则A= 0,其他 小圈
个顶点构成的圈(即三角形)是最稳定的,因此本文 考虑的圈将以三角形为基本单元。 随着经济的发展,许多城市面临着严重的交通 拥堵。 若出行者对自己要经过交通网络的路径、费 用、时间等能够以清晰地、直观地方式得到,则完成 任务的效率将会大大提高。 关于在复杂的交通网 络的条件下,研究合理的出行路径模型和算法,请 参见文献[2-9]。 基于多属性条件路径选择问题, 文献[2-9]以及目前掌握的材料中,均没有涉及对 于交通网路信息提取的概念格[10]可视化研究。 概念格建立了对象和属性之间的一种概念层 次结构,是数据分析和规则提取的一种有效工具。 Whitney [11]在 1935 年首次提出的拟阵已经被广泛 地应用于信息编码[12] 和网络安全[13] 等领域。 将拟 阵与概念格理论结合、图论[14-15]与概念格理论结合 来解决问题,已有许多成功的案例[16-21] 。 由于现实生活中,人们出行受多个属性条件的 限制,针对这些限制,经过研究发现 Kn 简单图中形 成三角形圈的一种特殊性质。 由此,可以对复杂的 交通网络进行分析、转化,形成 Kn 简单图。 进而,能 够建立网络模型,构建模型所对应的关联矩阵。 依 据 Kn 图所产生的特殊形式背景,建立概念格信息提 取方法。 从而,给出基于二元拟阵 Kn 图的一种建格 方法,并利用具体实例验证方法的正确性与有效性。 1 预备知识 本节主要介绍网络 Kn 图、拟阵和概念格一些定 义与相关结论。 有关图的基本概念和完全图的定 义,读者请参见文献[14]。 有关二元拟阵和图的拟 阵可表示性请参见文献[11]。 定义 1 [22] 设任意(无向)图 G = ( V,E),其中 顶点集 V = {v1 ,v2 ,…,vn },边集 E = { e1 ,e2 ,…,ee }。 用 mij表示顶点 vi 与边 ej 关联的次数,可能取值为 0,1,2,称所得矩阵 M(G) = (mij )n×e为图 G 的关联 矩阵。 定义 2 [14] V(G)= X∪Y,X∩Y = ⌀,X 中任二 项不相邻,Y 中任二项不相邻,则 G 为二部图;若 X 中每个顶点皆与 Y 中一切顶点相邻,则 G 为完全二 部图,记 Km,n ,其中 m = X ,n = Y 。 定义 3 [11] 设 M 是关于 E = { b1 ,b2 ,…,br,e1 , e2 ,…,eq}的一个拟阵,其中 B = {b1 ,b2 ,…,br}是 M 的一个基。 设 Cj 是 B∪{ej}所含的基本圈,定义 r× q 阶矩阵D = ( dij ),其中 dij = 1, 若 bi∈Cj 0, 其他 { ,则A= [Ir D]是 M 在模 2 域上的一个标准矩阵表示,其中 φ(bi)是 Ir 中第 i 列,而 φ(ej)是 D 中的第 j 列,1≤ i≤r,1≤j≤q。 引理 1 [14] 在一个具有 n 个顶点的无向完全图 中,包含的边数为 n(n-1) 2 。 定义 4 [17] 形式背景 K = (G,M,I)定义为一个 三元数组,其中 G 中的元素被称为对象,M 中的元 素被称为属性。 I⊆G×M,用 gIm 表示(g,m)∈I,即 对象 g 具有属性 m。 定义 5 [17] 形式背景(G,M,I)中的概念定义为 元素对(A,B),其中 A⊆G,B⊆M,A 称为概念的外 延,B 称为概念的内涵,并且满足以下条件: 1)B′= {a∈G ∀b∈B,aIb},A′ = {b∈M ∀a∈ A,aIb}; 2)A⊆A″,B⊆B″; 3)(∪ j∈J Aj)′=∩ j∈J Aj ′,(∪ j∈J Bj)′=∩ j∈J Bj ′。 定义 6 [17] 设(A1 ,B1 )、(A2 ,B2 )是 L(G,M,I) 中的两个概念,定义二元关系(A1 ,B1 )≤(A2 ,B2 )⇔ A1⊆A2⇔B1⊆B2 ,称(A1 ,B1 )是( A2 ,B2 ) 的子概念, (A2 ,B2 )是(A1 ,B1 )的父概念。 若不存在概念( A3 , B3 )使得(A1 ,B1 ) ≤(A3 ,B3 ) ≤(A2 ,B2 ) 成立,则称 (A1 ,B1 )是(A2 ,B2 )的直接子概念,(A2 ,B2 )是(A1 , B1 )的直接父概念。 不难证明这种父概念 - 子概念关系( 也称泛 化-特化关系)是 L(G,M,I)上的一个偏序关系。 事 实上 L(G,M,I)关于该偏序关系是一个完备格,称 为形式背景(G,M,I)的概念格,记为 L(G,M,I)。 引理 2 [17] 设( G,M,I) 是一个形式背景,则 L(G,M,I)关于上面定义的序“ ≤” 构成的是完备 格,其中上下确界由下式给出: ∨j∈J(Aj,Bj) = (∪ j∈J Aj ( ) ″, ∩ j∈J Bj) ∧j∈J(Aj,Bj) = (∩ j∈J Aj,(∪ j∈J Bj)″) 为了模型的建立和讨论表述简捷,给出如下几 个定义。 定义 7 含圈基:在 Kn 图中满足从一个顶点出 发,到其他 n-1 个顶点的相连接的边叫做含圈基。 定义 8 基顶点:在 Kn 图中满足从一个顶点出 发包含的所有相连的含圈基的顶点叫做基顶点。 定义 9 基最小圈:在一个三角形最小圈中,满 足一个最小圈中包含两个基的三角形圈,叫做基最 小圈。 ·334· 智 能 系 统 学 报 第 12 卷

第3期 毛华,等:利用二元拟阵K。图的一种建格方法 ·335· 模型的建立 很难给人们带来直接帮助,需要对交通运输网络进 行简化和直观化,得到一个简化的网络。若出行者 图论主要研究图的拓扑性质,为任何一个包含 需要计算出自己所居住的城市和其他任意两个城 某种二元关系系统提供一种分析和描述模型。众 市的距离和,即第1节定义9中的基最小圈,判断走 所周知,交通网络可以用图表示出来,也可把交通 哪个基最小圈距离和最短时,探究交通网络K图模 网络里的距离当作两点之间的权值加入进去。 型中的最小经济圈所需出行的路径距离就变得有 复杂网络中的交通网络对应图论里一类特殊 意义了。 的图结构,具有与应用相关的很多重要特征。对于 2.2模型的条件 一些网络中出现的复杂的网络,作如下处理。 设有个城市,每个城市看作一个顶点,两个城 1)对于两个顶点之间具有多重边的情况,选择 市之间有路可达时,用一条线相连接,建立城市网 其中权值最小的边。 络图。图中顶点用1,2,…,。表示,组成集合V= 2)当两个顶点之间的权值一样时,任意选择其 {1,2,…,心}。网络图中,之间有路径可达,记 中一条边,固定下来,成为最熟悉的一条道路。 相连接的边为em,将此交通网络图记为G=(V,E), 3)对于带环图的这种情况,因为实际问题考虑 得G为一个有限无向图。出行者从给定的一个顶 的是对于一个工厂的运输,自身运输没有任何实际 点城市,出发去办事,要求路径中必须经过两个顶 的意义。例如:如果是一家超市,自身对于自身运 点城市(除去给定城市顶点以外的其他任意两个顶 输也没有意义,所以不予考虑。 点城市),再返回到出发城市顶点1。由于出行者 具有重边或有环的图都可以转化为简单图应 走的道路为一个三角形,现在的问题是要选择一个 对出行问题,因此复杂网络图可以转化为简单图, 三角形在距离和花费的时间都少的三角形作为出 用以讨论相应的出行问题。由于在具有n个顶点的 行者的最终出行方案,这就需要找到所有可能的出 简单图中,K图结构最复杂,所以只要解决了K。图 行方法,换句话说,出行者需要出行前找到所有需 的出行问题,其他的简单图的出行问题将会迎刃而 要走过的路径和出行方案,以便从中选择最佳方 解。对于非K的n个顶点的简单图,因为它们是 案,这些方案对决策者综合路径距离、时间、花费决 K的子图,所以可以通过加边,使其成为K图,只 策时有重要的意义,可以帮助其更加直观、快速地 需将新加边的权值定义为0,采用本文的方法,完全 做决定,节约决策时间。 可以解决出行问题。基于以上的讨论,只需解决具 2.3问题的分析 有K,图这样的交通网络的出行问题,因此本文只研 交通城市之间的无向图G进行转化后是顶点 究K图。 为n的完全图,记G为K,图。因K,图对应的关联 现有n个城市,任意两个城市均由交通道路连 矩阵满足二元拟阵M,知定义7的含圈基满足定义 接。一位出行者要从自己所居住的城市去其他n-1 3的拟阵M,即实际生活中人们出行方案里的最小 个城市办事情,要求到达其他任意两个城市后再回 三角形圈。于是在K,图的二元拟阵的标准矩阵表 到自己所居住的城市,现在的问题是:如何找到以3 示如下:在对应组成基本圈的三条边下标记1,没有 个城市为三角形经济圈的一个出行方案。 组成基本圈的边下标记0,然后把得到的矩阵作为 首先建立一个网络模型,构建其关联矩阵。由 含0和1的形式背景。在上面进行概念格的探索和 于关联矩阵是一个0-1矩阵,信息提取中的任一个 证明时发现,在K图中将二元拟阵中的基本圈即定 形式背景可视为一个0-1矩阵,因此依据形式背景 义9的基最小圈,作为对象,每两个顶点之间相连的 的特殊性,建立概念格信息提取方法,进而找到人 边作为属性,建立形式背景,找寻概念会遵循一定 们所需的最适合出行方案。 的数学规律,运用此规律进行建格,速度很快。 2.1问题的提出 2.4模型的解决 在不同城市间构建现代化交通网络,实现城市 2.4.1K。图的建格模型 间交通一体化,将会极大方便交通出行。问题是: 根据定义3给出K图的标准矩阵表示。当顶 如何在众多出行方案中选取合适的方案,成为人们 点n=3时,根据引理1的公式得边数为3,含圈基的 出行前需要解决的问题。交通运输网络错综复杂, 个数为-1=2,与其中一个顶点相连接构成的基最
2 模型的建立 图论主要研究图的拓扑性质,为任何一个包含 某种二元关系系统提供一种分析和描述模型。 众 所周知,交通网络可以用图表示出来,也可把交通 网络里的距离当作两点之间的权值加入进去。 复杂网络中的交通网络对应图论里一类特殊 的图结构,具有与应用相关的很多重要特征。 对于 一些网络中出现的复杂的网络,作如下处理。 1)对于两个顶点之间具有多重边的情况,选择 其中权值最小的边。 2) 当两个顶点之间的权值一样时,任意选择其 中一条边,固定下来,成为最熟悉的一条道路。 3)对于带环图的这种情况,因为实际问题考虑 的是对于一个工厂的运输,自身运输没有任何实际 的意义。 例如:如果是一家超市,自身对于自身运 输也没有意义,所以不予考虑。 具有重边或有环的图都可以转化为简单图应 对出行问题,因此复杂网络图可以转化为简单图, 用以讨论相应的出行问题。 由于在具有 n 个顶点的 简单图中,Kn 图结构最复杂,所以只要解决了 Kn 图 的出行问题,其他的简单图的出行问题将会迎刃而 解。 对于非 Kn 的 n 个顶点的简单图,因为它们是 Kn 的子图,所以可以通过加边,使其成为 Kn 图,只 需将新加边的权值定义为 0,采用本文的方法,完全 可以解决出行问题。 基于以上的讨论,只需解决具 有 Kn 图这样的交通网络的出行问题,因此本文只研 究 Kn 图。 现有 n 个城市,任意两个城市均由交通道路连 接。 一位出行者要从自己所居住的城市去其他 n-1 个城市办事情,要求到达其他任意两个城市后再回 到自己所居住的城市,现在的问题是:如何找到以 3 个城市为三角形经济圈的一个出行方案。 首先建立一个网络模型,构建其关联矩阵。 由 于关联矩阵是一个 0-1 矩阵,信息提取中的任一个 形式背景可视为一个 0-1 矩阵,因此依据形式背景 的特殊性,建立概念格信息提取方法,进而找到人 们所需的最适合出行方案。 2.1 问题的提出 在不同城市间构建现代化交通网络,实现城市 间交通一体化,将会极大方便交通出行。 问题是: 如何在众多出行方案中选取合适的方案,成为人们 出行前需要解决的问题。 交通运输网络错综复杂, 很难给人们带来直接帮助,需要对交通运输网络进 行简化和直观化,得到一个简化的网络。 若出行者 需要计算出自己所居住的城市和其他任意两个城 市的距离和,即第 1 节定义 9 中的基最小圈,判断走 哪个基最小圈距离和最短时,探究交通网络 Kn图模 型中的最小经济圈所需出行的路径距离就变得有 意义了。 2.2 模型的条件 设有 n 个城市,每个城市看作一个顶点,两个城 市之间有路可达时,用一条线相连接,建立城市网 络图。 图中顶点用 v1 ,v2 ,…,vn 表示,组成集合 V = {v1 ,v2 ,…,vn }。 网络图中 vi,vj 之间有路径可达,记 相连接的边为 eij,将此交通网络图记为 G = (V,E), 得 G 为一个有限无向图。 出行者从给定的一个顶 点城市 v1 出发去办事,要求路径中必须经过两个顶 点城市(除去给定城市顶点以外的其他任意两个顶 点城市),再返回到出发城市顶点 v1 。 由于出行者 走的道路为一个三角形,现在的问题是要选择一个 三角形在距离和花费的时间都少的三角形作为出 行者的最终出行方案,这就需要找到所有可能的出 行方法,换句话说,出行者需要出行前找到所有需 要走过的路径和出行方案,以便从中选择最佳方 案, 这些方案对决策者综合路径距离、时间、花费决 策时有重要的意义,可以帮助其更加直观、快速地 做决定,节约决策时间。 2.3 问题的分析 交通城市之间的无向图 G 进行转化后是顶点 为 n 的完全图,记 G 为 Kn 图。 因 Kn 图对应的关联 矩阵满足二元拟阵 M,知定义 7 的含圈基满足定义 3 的拟阵 M,即实际生活中人们出行方案里的最小 三角形圈。 于是在 Kn 图的二元拟阵的标准矩阵表 示如下:在对应组成基本圈的三条边下标记 1,没有 组成基本圈的边下标记 0,然后把得到的矩阵作为 含 0 和 1 的形式背景。 在上面进行概念格的探索和 证明时发现,在 Kn 图中将二元拟阵中的基本圈即定 义 9 的基最小圈,作为对象,每两个顶点之间相连的 边作为属性,建立形式背景,找寻概念会遵循一定 的数学规律,运用此规律进行建格,速度很快。 2.4 模型的解决 2.4.1 Kn 图的建格模型 根据定义 3 给出 Kn 图的标准矩阵表示。 当顶 点 n = 3 时,根据引理 1 的公式得边数为 3,含圈基的 个数为 n-1 = 2,与其中一个顶点相连接构成的基最 第 3 期 毛华,等:利用二元拟阵 Kn 图的一种建格方法 ·335·
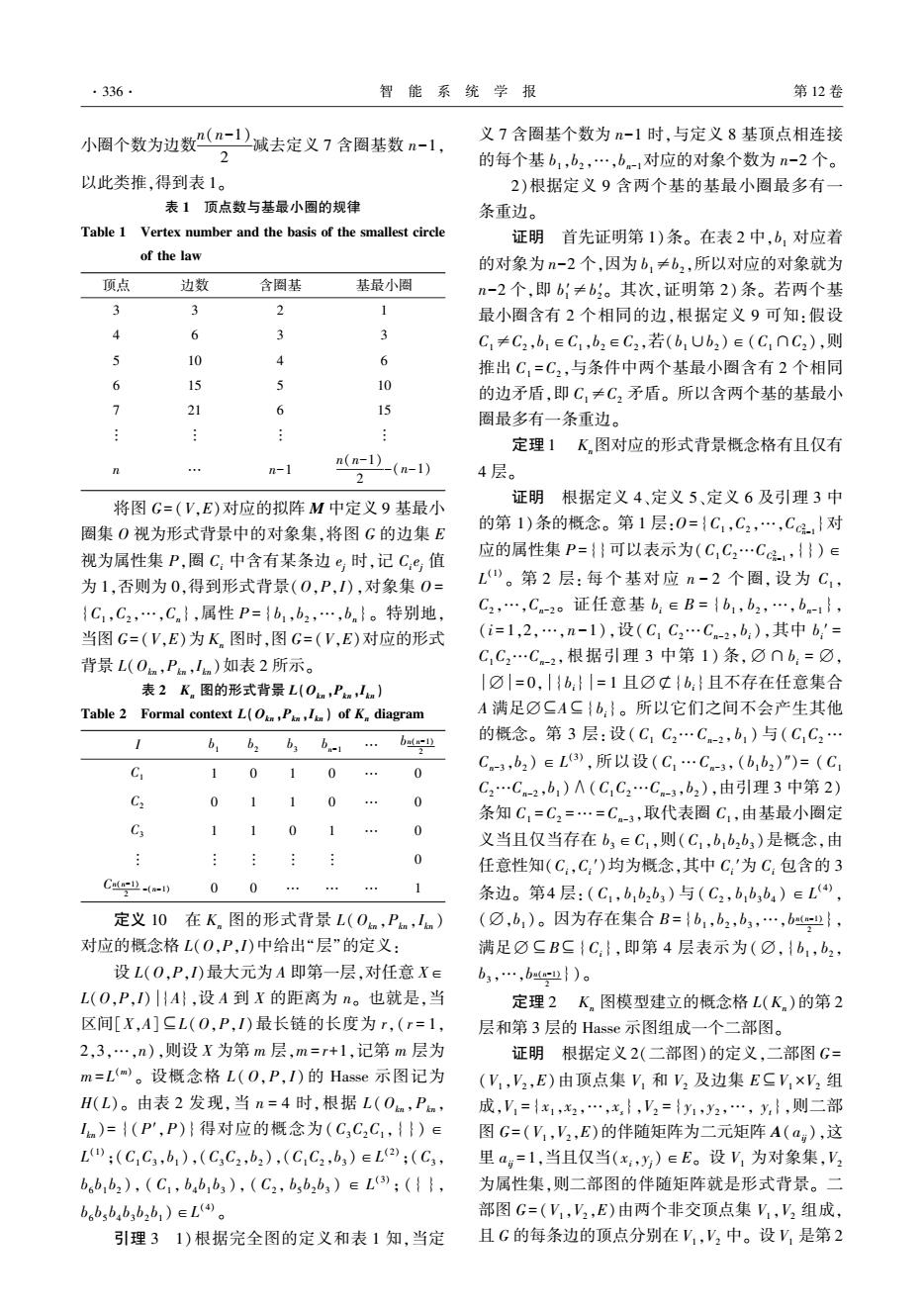
·336· 智能系统学报 第12卷 小圈个数为边数(-1)减去定义7含圈基数n-1, 义7含圈基个数为n-1时,与定义8基顶点相连接 2 的每个基b1,b2,…,b-1对应的对象个数为n-2个。 以此类推,得到表1。 2)根据定义9含两个基的基最小圈最多有 表1顶点数与基最小圈的规律 条重边。 Table 1 Vertex number and the basis of the smallest circle 证明首先证明第1)条。在表2中,b,对应着 of the law 的对象为n-2个,因为b,≠b2,所以对应的对象就为 顶点 边数 含圈基 基最小圈 n-2个,即b1≠b。其次,证明第2)条。若两个基 3 3 2 1 最小圈含有2个相同的边,根据定义9可知:假设 6 2 3 C1≠C2,b1∈C1,b2∈C2,若(b1Ub2)∈(C,∩C2),则 J 10 4 6 推出C,=C2,与条件中两个基最小圈含有2个相同 6 15 10 的边矛盾,即C,≠C,矛盾。所以含两个基的基最小 1 21 6 15 圈最多有一条重边。 定理1K图对应的形式背景概念格有且仅有 n-1 n(n-1)-(m-1) 2 4层。 证明根据定义4、定义5、定义6及引理3中 将图G=(V,E)对应的拟阵M中定义9基最小 圈集O视为形式背景中的对象集,将图G的边集E 的第1)条的概念。第1层:0={C1,C2,…,Cc,}对 视为属性集P,圈C:中含有某条边e时,记C,e值 应的属性集P={}可以表示为(C,C2Cc1,{})∈ 为1,否则为0,得到形式背景(0,P,I),对象集0= L)。第2层:每个基对应n-2个圈,设为C, {C1,C2,…,Cn},属性P={b,b2,…,bn}。特别地, C2,…,Cn-20证任意基b:∈B={b1,b2,…,bn-1}, 当图G=(V,E)为K,图时,图G=(V,E)对应的形式 (i=1,2,…,n-1),设(C1C2…Cn-2,b:),其中b;'= 背景L(0a,Pm,1n)如表2所示。 CC2…C。-2,根据引理3中第1)条,0nb,=⑦, 表2K.图的形式背景L(On,Pmla) |0|=0,{b:}|=1且☑¢{b:}且不存在任意集合 Table 2 Formal context L(O,PI)of K.diagram A满足☑二A二{b:}。所以它们之间不会产生其他 b b, ba-1 bn(n-1) 的概念。第3层:设(C1C2…Cn-2,b,)与(C,C2… 2 G 10 0 Cn3,b2)eL),所以设(C,…C。3,(b,b2)")=(C1 0 G 0 1 0 C2…Cn-2,b,)A(C1C2…Cn-3,b2),由引理3中第2) 0 条知C,=C2=…=C-3,取代表圈C,由基最小圈定 C3 1 1 0 1 0 义当且仅当存在b3∈C1,则(C1,bbb3)是概念,由 0 任意性知(C:,C,)均为概念,其中C:'为C:包含的3 Ca-D-(-1) 0 0 1 条边。第4层:(C1,b1b2b3)与(C2,b,b,b,)∈L4 定义10在K。图的形式背景L(Oa,Pa,Im) (0,b)。因为存在集合B={b1,b2,b3,…,b}, 对应的概念格L(0,P,)中给出“层”的定义: 满足0二BC{C},即第4层表示为(☑,{b,b2, 设L(0,P,I)最大元为A即第一层,对任意X∈ b3,…,b(a})。 L(O,P,I)|{A},设A到X的距离为n。也就是,当 定理2K,图模型建立的概念格L(K)的第2 区间[X,A]二L(O,P,)最长链的长度为r,(r=1, 层和第3层的Hasse示图组成一个二部图。 2,3,…,n),则设X为第m层,m=r+1,记第m层为 证明根据定义2(二部图)的定义,二部图G= m=L)。设概念格L(O,P,I)的Hasse示图记为 (V,V2,E)由顶点集V,和V及边集ECV,×V2组 H(L)。由表2发现,当n=4时,根据L(Oa,Pn, 成,={x1,x2,…,x},2={y1,y2,…,y},则二部 In)={(P',P)}得对应的概念为(C3C2C1,{})∈ 图G=(V,V2,E)的伴随矩阵为二元矩阵A(a),这 L;(C,C3,b1),(C,C2,b2),(C,C2,b)eL2;(C3, 里a=1,当且仅当(x:,y)∈E。设V1为对象集,V bsbb2),(C1,b,b,b3),(C2,bbb3)∈L):({, 为属性集,则二部图的伴随矩阵就是形式背景。二 bsb,b,bb,b1)∈L。 部图G=(V,V2,E)由两个非交顶点集V,V2组成, 引理31)根据完全图的定义和表1知,当定 且G的每条边的顶点分别在V,V2中。设Y,是第2
小圈个数为边数 n(n-1) 2 减去定义 7 含圈基数 n-1, 以此类推,得到表 1。 表 1 顶点数与基最小圈的规律 Table 1 Vertex number and the basis of the smallest circle of the law 顶点 边数 含圈基 基最小圈 3 3 2 1 4 6 3 3 5 10 4 6 6 15 5 10 7 21 6 15 ︙ ︙ ︙ ︙ n … n-1 n(n-1) 2 -(n-1) 将图 G = (V,E)对应的拟阵 M 中定义 9 基最小 圈集 O 视为形式背景中的对象集,将图 G 的边集 E 视为属性集 P,圈 Ci 中含有某条边 ej 时,记 Ci ej 值 为 1,否则为 0,得到形式背景(O,P,I),对象集 O = {C1 ,C2 ,…,Cn },属性 P = {b1 ,b2 ,…,bn }。 特别地, 当图 G = (V,E)为 Kn 图时,图 G = (V,E)对应的形式 背景 L(Okn ,Pkn ,Ikn )如表 2 所示。 表 2 Kn 图的形式背景 L(Okn ,Pkn ,Ikn ) Table 2 Formal context L(Okn ,Pkn ,Ikn ) of Kn diagram I b1 b2 b3 bn-1 … bn(n-1) 2 C1 1 0 1 0 … 0 C2 0 1 1 0 … 0 C3 1 1 0 1 … 0 ︙ ︙ ︙ ︙ ︙ 0 Cn(n-1) 2 -(n-1) 0 0 … … … 1 定义 10 在 Kn 图的形式背景 L(Okn ,Pkn ,Ikn ) 对应的概念格 L(O,P,I)中给出“层”的定义: 设 L(O,P,I)最大元为 A 即第一层,对任意 X∈ L(O,P,I) {A},设 A 到 X 的距离为 n。 也就是,当 区间[X,A]⊆L(O,P,I)最长链的长度为 r,( r = 1, 2,3,…,n),则设 X 为第 m 层,m = r+1,记第 m 层为 m = L (m) 。 设概念格 L (O,P,I) 的 Hasse 示图记为 H(L)。 由表 2 发现,当 n = 4 时,根据 L (Okn ,Pkn , Ikn )= {(P′,P)} 得对应的概念为( C3C2C1 ,{ }) ∈ L (1) ;(C1C3 ,b1 ),(C3C2 ,b2 ),(C1C2 ,b3 )∈L (2) ;(C3 , b6 b1 b2 ), ( C1 , b4 b1 b3 ), ( C2 , b5 b2 b3 ) ∈ L (3) ; ({ }, b6 b5 b4 b3 b2 b1 )∈L (4) 。 引理 3 1)根据完全图的定义和表 1 知,当定 义 7 含圈基个数为 n-1 时,与定义 8 基顶点相连接 的每个基 b1 ,b2 ,…,bn-1对应的对象个数为 n-2 个。 2)根据定义 9 含两个基的基最小圈最多有一 条重边。 证明 首先证明第 1)条。 在表 2 中,b1 对应着 的对象为 n-2 个,因为 b1≠b2 ,所以对应的对象就为 n-2 个,即 b1 ′≠b2 ′。 其次,证明第 2) 条。 若两个基 最小圈含有 2 个相同的边,根据定义 9 可知:假设 C1≠C2 ,b1∈C1 ,b2∈C2 ,若(b1∪b2 )∈(C1∩C2 ),则 推出 C1 =C2 ,与条件中两个基最小圈含有 2 个相同 的边矛盾,即 C1≠C2 矛盾。 所以含两个基的基最小 圈最多有一条重边。 定理 1 Kn图对应的形式背景概念格有且仅有 4 层。 证明 根据定义 4、定义 5、定义 6 及引理 3 中 的第 1)条的概念。 第 1 层:O= {C1 ,C2 ,…,CC2 n-1 }对 应的属性集 P = {}可以表示为(C1C2…CC2 n-1 ,{ })∈ L (1) 。 第 2 层: 每 个 基 对 应 n - 2 个 圈, 设 为 C1 , C2 ,…,Cn-2 。 证任意基 bi ∈B = { b1 , b2 ,…, bn-1 }, (i = 1,2,…,n-1),设(C1 C2…Cn-2 ,bi ),其中 bi ′ = C1C2…Cn-2 ,根据引理 3 中第 1) 条,⌀∩ bi = ⌀, ⌀ = 0, {bi} = 1 且⌀⊄{bi}且不存在任意集合 A 满足⌀⊆A⊆{ bi}。 所以它们之间不会产生其他 的概念。 第 3 层:设( C1 C2…Cn-2 , b1 ) 与( C1C2 … Cn-3 ,b2 ) ∈L (3) ,所以设( C1 …Cn-3 , (b1 b2 )″)= ( C1 C2…Cn-2 ,b1 )∧(C1C2…Cn-3 ,b2 ),由引理 3 中第 2) 条知 C1 =C2 = … = Cn-3 ,取代表圈 C1 ,由基最小圈定 义当且仅当存在 b3∈C1 ,则(C1 ,b1 b2 b3 )是概念,由 任意性知(Ci,Ci ′)均为概念,其中 Ci ′为 Ci 包含的 3 条边。 第4 层:( C1 ,b1 b2 b3 ) 与( C2 , b1 b3 b4 ) ∈L (4) , (⌀,b1 )。 因为存在集合 B = {b1 ,b2 ,b3 ,…,bn(n-1) 2 }, 满足⌀⊆B⊆{Ci },即第 4 层表示为(⌀,{ b1 ,b2 , b3 ,…,bn(n-1) 2 })。 定理 2 Kn 图模型建立的概念格 L(Kn )的第 2 层和第 3 层的 Hasse 示图组成一个二部图。 证明 根据定义 2(二部图)的定义,二部图 G = (V1 ,V2 ,E)由顶点集 V1 和 V2 及边集 E⊆V1 ×V2 组 成,V1 = {x1 ,x2 ,…,xs},V2 = { y1 ,y2 ,…, yt},则二部 图 G = (V1 ,V2 ,E)的伴随矩阵为二元矩阵 A(aij),这 里 aij = 1,当且仅当(xi,yj)∈E。 设 V1 为对象集,V2 为属性集,则二部图的伴随矩阵就是形式背景。 二 部图 G = (V1 ,V2 ,E)由两个非交顶点集 V1 ,V2 组成, 且 G 的每条边的顶点分别在 V1 ,V2 中。 设 V1 是第 2 ·336· 智 能 系 统 学 报 第 12 卷

第3期 毛华,等:利用二元拟阵K。图的一种建格方法 ·337. 层概念的集合,V2是第3层概念的集合,则在K。图 为K.时,顶点数为n,与基顶点相连的边为n-1,即 中概念之间满足定义6,(C1,b1)≤(C2,b2)一C, 第2层的概念为n-1个,根据属性b1,b2,…,bn-找 C(台b,二b,),根据子概念-父概念的关系建立连线 到所对应的基最小圈对象。 是一个二部图,如图1所示。 3)找第3层的概念,根据完全图K的特点,基 (C.C;b (C,C b,) (CCb) 最小圈的个数为(-1)-(n-1),即第3层有概念 2 n(n-1)-(n-1)个,由对象C,C2,…,Cg(-,找 ● (Cbbb) (Cbbb) (C,6bb.) 到所对应的属性。 4)第1层中的元(概念),与且仅与第2层的每 图1K,图的二部图 一个元分别连线,第4层的元与且仅与第3层的每 Fig.1 Bipartite graph of K,diagram 个元分别连线,第2层的元与第3层的元之间的 再把第1层和第4层概念(0,{})和({},P)加 连线关系可以根据定理2进行。这样就可以得到所 进图1,根据定理1建立概念格得Hasse示图,如图 有应该存在的连线。即根据定义6和引理2的偏序 2所示。Hasse图是利用概念之间的泛化和特化进 关系(C1,b)≤(C2,b2)台C1SC2(台b,≤b,),满足 行绘制的,由于概念格的完备性,概念格确定了,其 概念格子概念-父概念的关系,把第1层的概念(0, Hasse图也唯一确定了。概念格最上层是全概念, {})与第2层的概念建立连线,第4层的概念({}, 最下层是空概念。Hasse图中的边分别连接在直接 P)与第3层概念建立连线加入到步骤2)和3)组成 父概念和直接子概念之间。 的二部图中。 (C.C.C) 2.4.3算法的复杂度 根据形式背景的特殊性,此处得到的概念格有 且仅有4层。 (C.C.b)O ○CC,b,) ○(CCb) 第1层的概念和第四层的概念分别是(O,{}) 和({},P)。 第2层的概念与基顶点连接的边个数为n-1(n (C..bb.b) ○Cb,b,b) ○(Cb,b,b,) 表示顶点数)。 第3层的概念根据K,图所产生的基最小圈个 数N来决定,N=(n1)-(n-1)。根据第2层的概 (,bbbbbb) 2 图2K,图的概念格 念加入属性,即K。图的边,根据属性b1,b2,…,bn- Fig.2 Concept lattice of K diagram 找到所对应的基最小圈对象,知寻找的次数为W: 第3层加入基最小圈即概念的对象时,即K图里的 根据K,图的格结构,利用数学归纳法分别对 K图、K。图、K图进行建格,得出K图建立概念格 基最小圈,根据对象C,C2,…,C-),找到所 的一个算法过程。 对应的属性,可知寻找的次数为nN。即第2层和第 3层运算次数为nN+nN=2nN,复杂度为0(2nn2), 2.4.2算法过程 也就是0(n3)。 通过对特殊限制K图的规律发现,满足K图 与定义5和定义6找寻概念的方式(即参考文 二元标准矩阵特点的都可以建成一个Hasse示图。 献[22]中13页概念格的生成算法1)相比,本文提 对于具有这种特定形式背景的概念,用上面的建格 出的方法更有效。因为,如果存在1G1个对象,1M 方法进行建格,速度很快。下面给出对象是基最小 个属性,那么相应的概念格将可能包含2G或2m 圈,属性是边的形式背景的建格过程。 个概念,计算量太大。而本文构造的概念的算法方 输入形式背景(0,P,I)。 式,由于具有一定的规律性,大大减少了计算量。 输出集合C,(0,P,I)所有的概念。 1)C:={P',P}初始化属性集合B=☑。 3应用实例 2)找第2层的概念,根据规律知道,当完全图 超市里冷冻猪肉和冷鲜猪肉因储存时间的长
层概念的集合,V2 是第 3 层概念的集合,则在 Kn 图 中概念之间满足定义 6,(C1 ,b1 )≤(C2 ,b2 )⇔C1⊆ C2(⇔b2⊆b1 ),根据子概念-父概念的关系建立连线 是一个二部图,如图 1 所示。 图 1 K4 图的二部图 Fig.1 Bipartite graph of K4 diagram 再把第 1 层和第 4 层概念(O,{})和({},P)加 进图 1,根据定理 1 建立概念格得 Hasse 示图,如图 2 所示。 Hasse 图是利用概念之间的泛化和特化进 行绘制的,由于概念格的完备性,概念格确定了,其 Hasse 图也唯一确定了。 概念格最上层是全概念, 最下层是空概念。 Hasse 图中的边分别连接在直接 父概念和直接子概念之间。 图 2 K4 图的概念格 Fig.2 Concept lattice of K4 diagram 根据 K4 图的格结构,利用数学归纳法分别对 K5 图、K6 图、Kn 图进行建格,得出 Kn 图建立概念格 的一个算法过程。 2.4.2 算法过程 通过对特殊限制 Kn 图的规律发现,满足 Kn 图 二元标准矩阵特点的都可以建成一个 Hasse 示图。 对于具有这种特定形式背景的概念,用上面的建格 方法进行建格,速度很快。 下面给出对象是基最小 圈,属性是边的形式背景的建格过程。 输入 形式背景(O,P,I)。 输出 集合 C,(O,P,I)所有的概念。 1)C:= {P′,P}初始化属性集合 B =⌀。 2)找第 2 层的概念,根据规律知道,当完全图 为 Kn 时,顶点数为 n,与基顶点相连的边为 n-1,即 第 2 层的概念为 n-1 个,根据属性 b1 ,b2 ,…,bn-1找 到所对应的基最小圈对象。 3)找第 3 层的概念,根据完全图 Kn 的特点,基 最小圈的个数为 n(n-1) 2 -( n-1),即第 3 层有概念 n(n-1) 2 -(n-1)个,由对象 C1 ,C2 ,…,Cn(n-1) 2 -(n-1) ,找 到所对应的属性。 4)第 1 层中的元(概念),与且仅与第 2 层的每 一个元分别连线,第 4 层的元与且仅与第 3 层的每 一个元分别连线,第 2 层的元与第 3 层的元之间的 连线关系可以根据定理 2 进行。 这样就可以得到所 有应该存在的连线。 即根据定义 6 和引理 2 的偏序 关系(C1 ,b1 )≤(C2 ,b2 )⇔C1⊆C2(⇔b2⊆b1 ),满足 概念格子概念-父概念的关系,把第 1 层的概念(O, {})与第 2 层的概念建立连线,第 4 层的概念({ }, P)与第 3 层概念建立连线加入到步骤 2)和 3)组成 的二部图中。 2.4.3 算法的复杂度 根据形式背景的特殊性,此处得到的概念格有 且仅有 4 层。 第 1 层的概念和第四层的概念分别是(O,{ }) 和({},P)。 第 2 层的概念与基顶点连接的边个数为 n-1(n 表示顶点数)。 第 3 层的概念根据 Kn 图所产生的基最小圈个 数 N 来决定,N= n(n-1) 2 -(n-1)。 根据第 2 层的概 念加入属性,即 Kn 图的边,根据属性 b1 ,b2 ,…,bn-1 找到所对应的基最小圈对象,知寻找的次数为 nN; 第 3 层加入基最小圈即概念的对象时,即 Kn 图里的 基最小圈,根据对象 C1 ,C2 ,…,Cn(n+1) 2 -(b-1) ,找到所 对应的属性,可知寻找的次数为 nN。 即第 2 层和第 3 层运算次数为 nN+nN = 2nN,复杂度为 O(2nn 2 ), 也就是 O(n 3 )。 与定义 5 和定义 6 找寻概念的方式(即参考文 献[22]中 13 页概念格的生成算法 1)相比,本文提 出的方法更有效。 因为,如果存在| G |个对象, | M | 个属性,那么相应的概念格将可能包含 2 | G| 或 2 | M| 个概念,计算量太大。 而本文构造的概念的算法方 式,由于具有一定的规律性,大大减少了计算量。 3 应用实例 超市里冷冻猪肉和冷鲜猪肉因储存时间的长 第 3 期 毛华,等:利用二元拟阵 Kn 图的一种建格方法 ·337·