
奇偶编码校验 USTC 在被传送的n位代码(bn.1bn-2bbo)上增加一位 校验位P,,将原数据和得到的奇(偶)校验位 一起进行存取或传送(即传送Pbn-bn-2bbo)。 吗校避=I1+I2+“+Ii i=12,"q 奇嵌盟:r=I+I2十“+I+1 i=12“q ·码距? ·可以发现“奇数”个错:一位出错的慨率高 ·只能检错,不能纠错
奇偶编码校验 • 在被传送的n位代码(bn-1bn-2 ...b1b0 )上增加一位 校验位P,将原数据和得到的奇(偶)校验位 一起进行存取或传送(即传送Pbn-1bn-2 ...b1b0 )。 • 码距? • 可以发现“奇数”个错:一位出错的概率高 • 只能检错,不能纠错
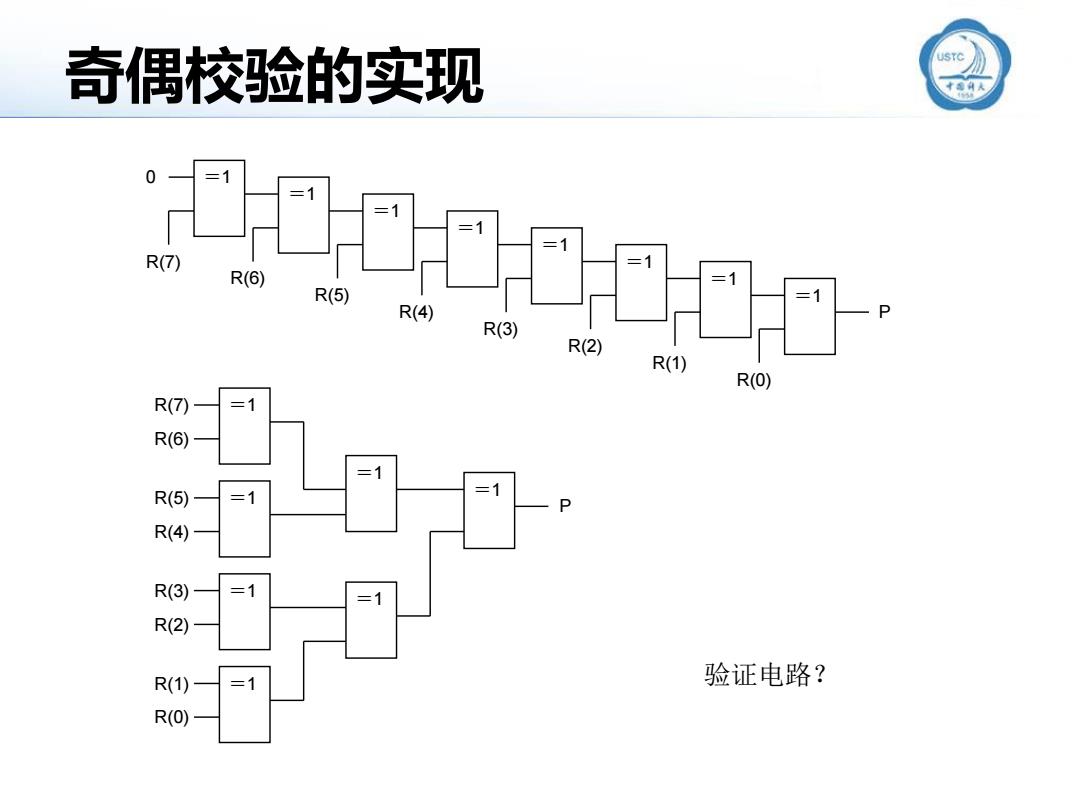
奇偶校验的实现 内 =1 =1 R(7) 三1 R(6) R(5) R(4) R(3) R(2) R(1) R(O) R(7) =1 R(6) =1 R(5) =1 R(4) R(3) =1 三1 R(2) R(1) 验证电路? R(O)
奇偶校验的实现 0 =1 R(7) =1 R(6) =1 R(5) =1 R(4) =1 R(3) =1 R(2) =1 R(1) =1 R(0) P =1 R(6) R(7) =1 R(4) R(5) =1 R(2) R(3) =1 R(0) R(1) =1 =1 =1 P 验证电路?

奇偶校验的实现(续) 力 entity IPAR is generic(PROP_DEL:time); port(R:in Std_logic_vector(7 down to 0);P:out Std_logic); end IPAR; architecture LOOP4 of IPAR is signal CLOCK:Std_logic :='0'; begin OPAR:process(R) variable X:Std_logic; begin X=0; for I in 7 downto 0 loop X :X xor R(I); end loop; P<=X after PROP_DEL; end process; end LOOP4;
奇偶校验的实现(续) entity IPAR is generic(PROP_DEL: time); port(R: in Std_logic_vector( 7 down to 0); P: out Std_logic); end IPAR; architecture LOOP4 of IPAR is signal CLOCK: Std_logic := ‘0’; begin OPAR: process(R) variable X: Std_logic; begin X := ‘0’; for I in 7 downto 0 loop X := X xor R(I); end loop; P <= X after PROP_DEL; end process; end LOOP4;
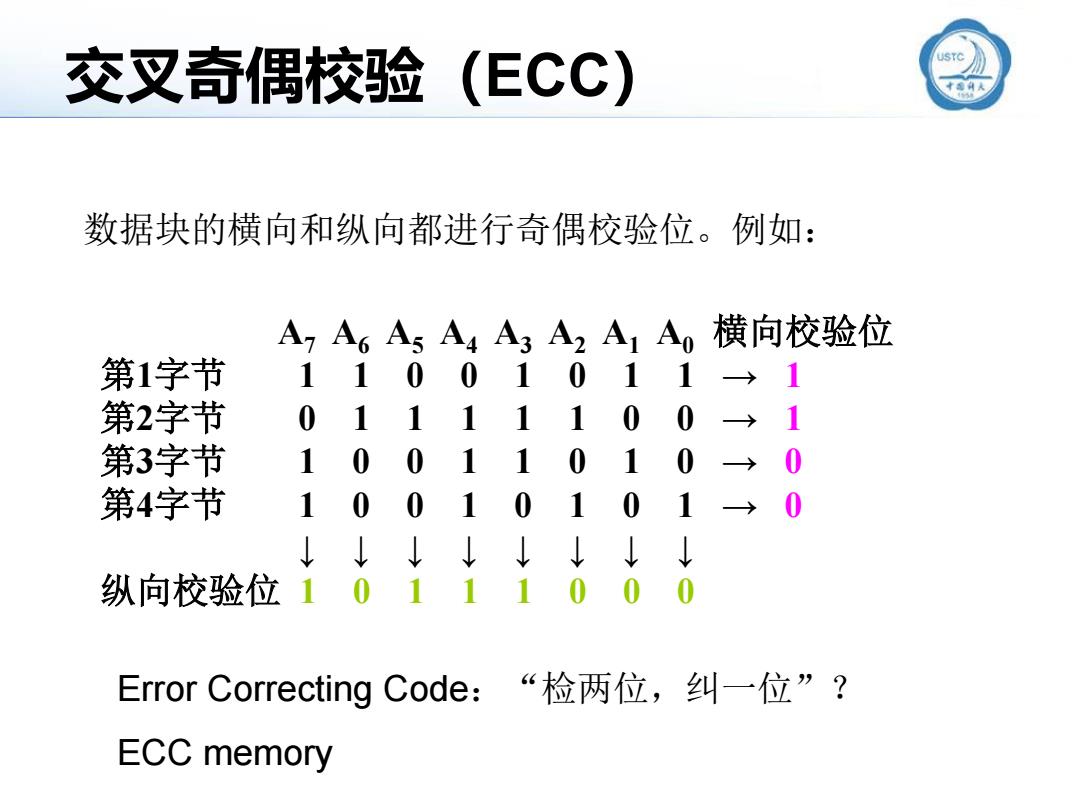
交叉奇偶校验(ECC) 数据块的横向和纵向都进行奇偶校验位。例如: A,A6AA4A3A2A1A横向校验位 第1字节 1100101 第2字节 0 第3字节 1 0 0 0 0 第4字节 1 0 1 1 0 1 0 纵向校验位 0 1 0 0 0 Error Correcting Code:“检两位,纠一位”? ECC memory
数据块的横向和纵向都进行奇偶校验位。例如: A7 A6 A5 A4 A3 A2 A1 A0 横向校验位 第1字节 1 1 0 0 1 0 1 1 → 1 第2字节 0 1 1 1 1 1 0 0 → 1 第3字节 1 0 0 1 1 0 1 0 → 0 第4字节 1 0 0 1 0 1 0 1 → 0 ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ 纵向校验位 1 0 1 1 1 0 0 0 Error Correcting Code:“检两位,纠一位”? ECC memory 交叉奇偶校验(ECC)
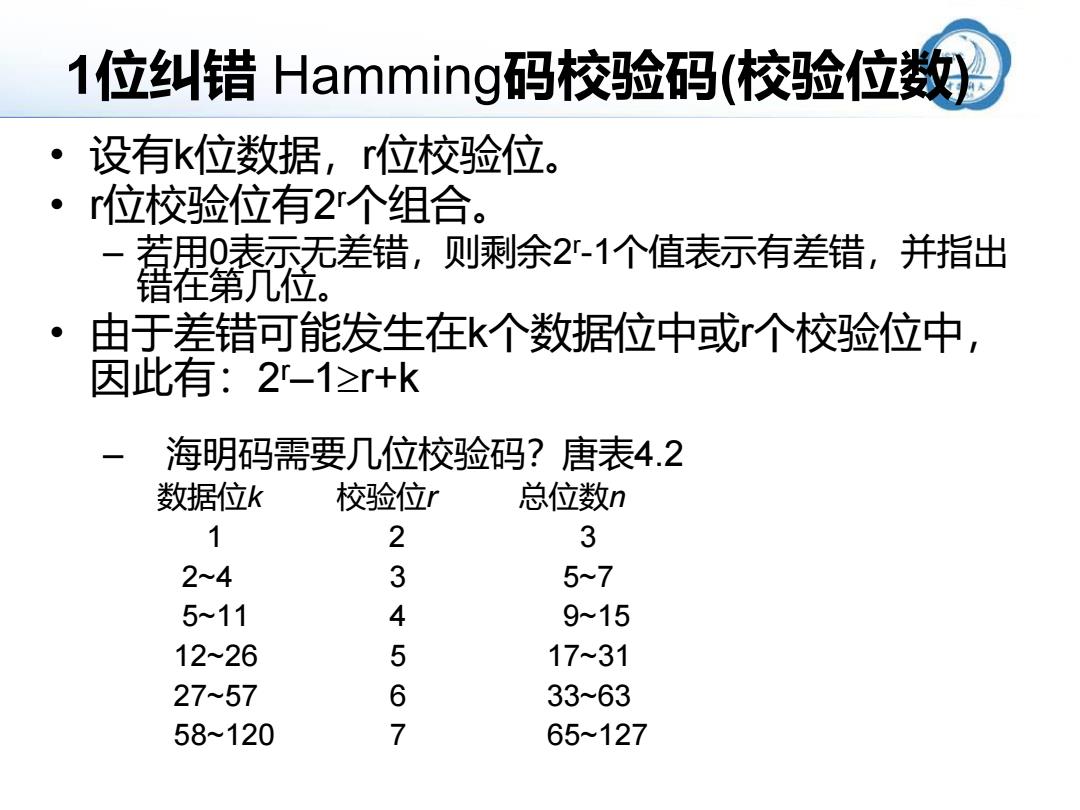
1位纠错Hamming码校验码(校验位数 ·设有k位数据,位校验位。 r位校验位有2r个组合。 若用0表示无差错,则剩余2-1个值表示有差错,并指出 错在第几位。 由于差错可能发生在k个数据位中或个校验位中, 因此有:2-1≥+k 海明码需要几位校验码?唐表4.2 数据位k 校验位r 总位数n 1 2 3 2~4 3 5~7 5~11 4 9~15 12~26 5 17~31 27~57 6 33~63 58~120 7 65~127
1位纠错 Hamming码校验码(校验位数) – 海明码需要几位校验码?唐表4.2 数据位k 校验位r 总位数n 1 2 3 2~4 3 5~7 5~11 4 9~15 12~26 5 17~31 27~57 6 33~63 58~120 7 65~127 • 设有k位数据,r位校验位。 • r位校验位有2 r个组合。 – 若用0表示无差错,则剩余2 r -1个值表示有差错,并指出 错在第几位。 • 由于差错可能发生在k个数据位中或r个校验位中, 因此有:2 r–1r+k