
1.正交变换的定义 2.第一类和第二类正交变换 二、具体要求 1.熟悉正交变换的定义 2.熟悉第一类和第二类正交变换 第五节子空间 一、讲授内容 1.子空间正交的定义及其判定 2.子空间的正交补 二、具体要求 1.掌握子空间正交的定义及其判定 2.了解正交补及相关结论 第六节实对称矩阵的标准形 一、讲授内容 1.实对称矩阵的标准形 2.对称变换 二、具体要求 1.掌握实对称矩阵特征向量的性质 2.会用正交替换将实对称矩阵化成标准形 第七节向量到子空间的距离和最小二乘法 一、讲授内容 1.向量间距离和向量到子空间的距离的定义 2.最小二乘法 二、具体要求 1.了解向量间距离和向量到子空间的距离的性质 2.了解最小二乘法及其简单应用 第八节酉空间介绍 一、讲授内容 1.酉矩阵和酉空间的定义 35
35 1. 正交变换的定义 2. 第一类和第二类正交变换 二、具体要求 1. 熟悉正交变换的定义 2. 熟悉第一类和第二类正交变换 第五节 子空间 一、讲授内容 1. 子空间正交的定义及其判定 2. 子空间的正交补 二、具体要求 1. 掌握子空间正交的定义及其判定 2. 了解正交补及相关结论 第六节 实对称矩阵的标准形 一、讲授内容 1. 实对称矩阵的标准形 2. 对称变换 二、具体要求 1. 掌握实对称矩阵特征向量的性质 2. 会用正交替换将实对称矩阵化成标准形 第七节 向量到子空间的距离和最小二乘法 一、讲授内容 1. 向量间距离和向量到子空间的距离的定义 2. 最小二乘法 二、具体要求 1. 了解向量间距离和向量到子空间的距离的性质 2. 了解最小二乘法及其简单应用 第八节 酉空间介绍 一、讲授内容 1. 酉矩阵和酉空间的定义

2.埃尔米特(Hermite))矩阵的定义和酉空间的对称变换 二、具体要求 1.了解酉矩阵和酉空间的概念 2.了解埃尔米特(Hermite)矩阵的概念和酉空间的对称变换及相关结果 第九章 双线性函数简介 重点:线性函数的概念, 对偶空间的概念,双线性函数的概念。 难点:对偶空间的概念。 第一节线性函数 一、讲授内容 1.线性函数的定义 2.线性函数的基本性质 二、具体要求 1.了解线性函数的概念 2.了解线性函数的基本性质 第二节对偶空间 一、讲授内容 1.对偶空间的定义 2.对偶空间的简单性质 二、具体要求 1.了解对偶空间的概念 2.了解对偶空间的简单性质 第三节双线性函数 一、讲授内容 1.双线性函数的定义 2.双线性函数的简单性质 二、具体要求 1.了解双线性函数的概念 2.了解双线性函数的简单性质 (二)教学方法与手段 主要采取课堂讲授式教学,习题课、课外辅导为辅。注意引导启发学生:使用板书加多媒体课件。 36
36 2. 埃尔米特(Hermite)矩阵的定义和酉空间的对称变换 二、具体要求 1. 了解酉矩阵和酉空间的概念 2. 了解埃尔米特(Hermite)矩阵的概念和酉空间的对称变换及相关结果 第九章 双线性函数简介 第一节 线性函数 一、讲授内容 1. 线性函数的定义 2. 线性函数的基本性质 二、具体要求 1. 了解线性函数的概念 2. 了解线性函数的基本性质 第二节 对偶空间 一、讲授内容 1. 对偶空间的定义 2. 对偶空间的简单性质 二、具体要求 1. 了解对偶空间的概念 2. 了解对偶空间的简单性质 第三节 双线性函数 一、讲授内容 1. 双线性函数的定义 2. 双线性函数的简单性质 二、具体要求 1. 了解双线性函数的概念 2. 了解双线性函数的简单性质 (二)教学方法与手段 主要采取课堂讲授式教学,习题课、课外辅导为辅。注意引导启发学生;使用板书加多媒体课件。 重点:线性函数的概念, 对偶空间的概念, 双线性函数的概念。 难点: 对偶空间的概念
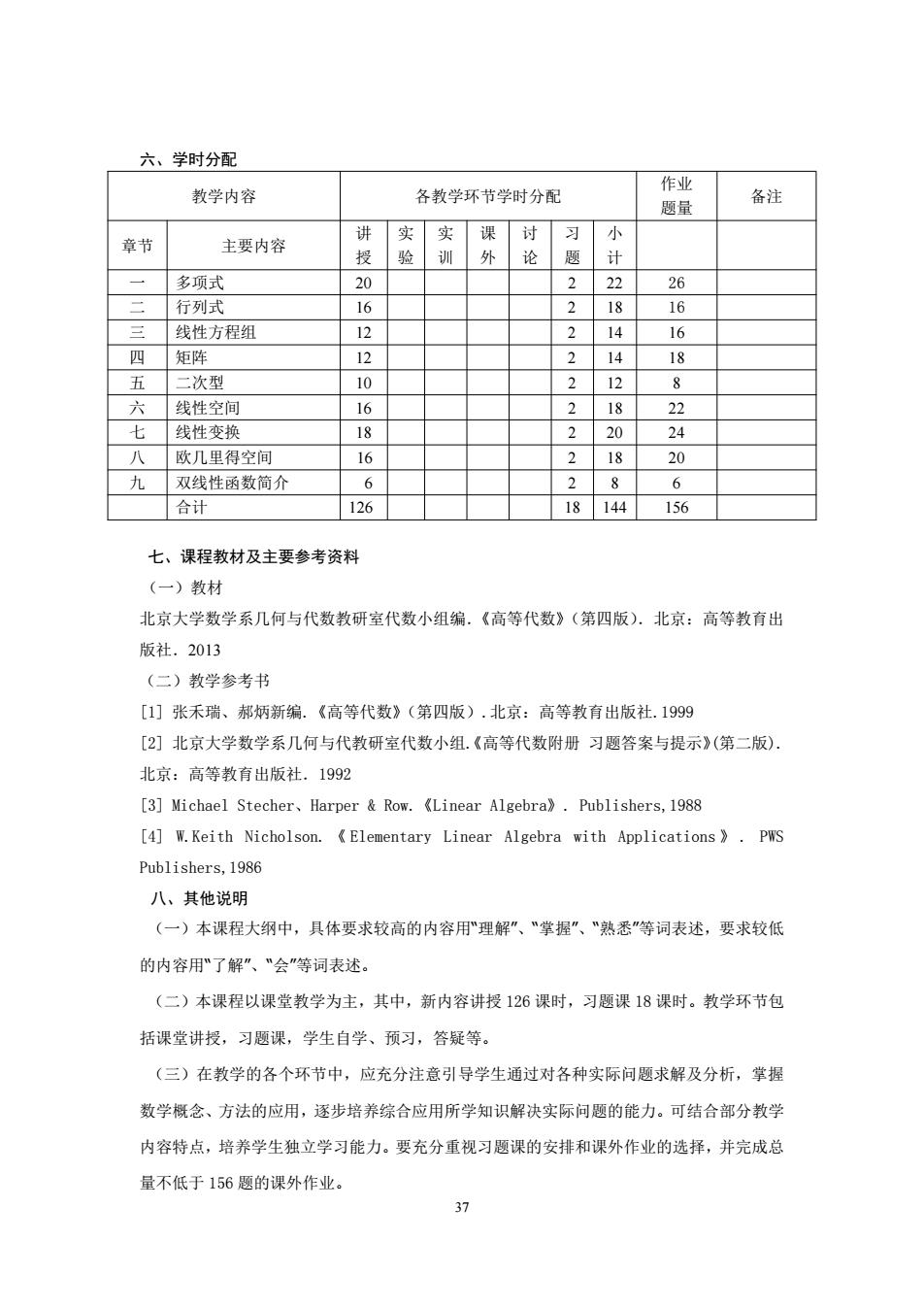
六、学时分配 作业 教学内容 各教学环节学时分配 题量 备注 讲 实 实 课 讨 习 小 章节 主要内容 授 验 训 外 论 题 计 一 多项式 20 2 22 26 行列式 16 18 16 三 线性方程组 12 2 14 16 四 矩阵 12 2 14 18 五 二次型 10 2 12 8 六 线性空间 16 218 22 七 线性变换 18 2 20 24 八 欧几里得空间 16 2 18 20 九 双线性函数简介 6 2 8 6 合计 126 18144 156 七、课程教材及主要参考资料 (一)教材 北京大学数学系几何与代数教研室代数小组编.《高等代数》(第四版).北京:高等教育出 版社.2013 (二)教学参考书 [1]张禾瑞、郝炳新编.《高等代数》(第四版).北京:高等教有出版社.1999 [2]北京大学数学系几何与代教研室代数小组.《高等代数附册习题答案与提示》(第二版), 北京:高等教育出版社.1992 [3]Michael Stecher,Harper Row.Linear Algebra).Publishers,1988 [4]W.Keith Nicholson.Elementary Linear Algebra with Applications >PWS Publishers,1986 八、其他说明 (一)本课程大纲中,具体要求较高的内容用理解”、“掌握”、"熟悉”等词表述,要求较低 的内容用"了解”、“会"等词表述。 (二)本课程以课堂教学为主,其中,新内容讲授126课时,习题课18课时。教学环节包 括课堂讲授,习题课,学生自学、预习,答疑等。 (三)在教学的各个环节中,应充分注意引导学生通过对各种实际问题求解及分析,掌握 数学概念、方法的应用,逐步培养综合应用所学知识解决实际问题的能力。可结合部分教学 内容特点,培养学生独立学习能力。要充分重视习题课的安排和课外作业的选择,并完成总 量不低于156题的课外作业。 37
37 六、学时分配 教学内容 各教学环节学时分配 作业 题量 备注 章节 主要内容 讲 授 实 验 实 训 课 外 讨 论 习 题 小 计 一 多项式 20 2 22 26 二 行列式 16 2 18 16 三 线性方程组 12 2 14 16 四 矩阵 12 2 14 18 五 二次型 10 2 12 8 六 线性空间 16 2 18 22 七 线性变换 18 2 20 24 八 欧几里得空间 16 2 18 20 九 双线性函数简介 6 2 8 6 合计 126 18 144 156 七、课程教材及主要参考资料 (一)教材 北京大学数学系几何与代数教研室代数小组编.《高等代数》(第四版).北京:高等教育出 版社.2013 (二)教学参考书 [1] 张禾瑞、郝炳新编.《高等代数》(第四版).北京:高等教育出版社.1999 [2] 北京大学数学系几何与代教研室代数小组.《高等代数附册 习题答案与提示》(第二版). 北京:高等教育出版社.1992 [3] Michael Stecher、Harper & Row.《Linear Algebra》. Publishers,1988 [4] W.Keith Nicholson. 《 Elementary Linear Algebra with Applications 》 . PWS Publishers,1986 八、其他说明 (一)本课程大纲中,具体要求较高的内容用“理解”、“掌握”、“熟悉”等词表述,要求较低 的内容用“了解”、“会”等词表述。 (二)本课程以课堂教学为主,其中,新内容讲授 126 课时,习题课 18 课时。教学环节包 括课堂讲授,习题课,学生自学、预习,答疑等。 (三)在教学的各个环节中,应充分注意引导学生通过对各种实际问题求解及分析,掌握 数学概念、方法的应用,逐步培养综合应用所学知识解决实际问题的能力。可结合部分教学 内容特点,培养学生独立学习能力。要充分重视习题课的安排和课外作业的选择,并完成总 量不低于 156 题的课外作业

(四)在教学中,应注重现代化教学手段的应用,可根据具体的教学内容和要求,采用板 书和多媒体课件相结合的教学方式,实施讲授法、启发引导式法、设疑讨论式法、案例教学 法、翻转课堂或微课等进行教学,加强教学互动,充分发挥教与学两个方面的积极性,保证 总体大纲的贯彻执行。 38
38 (四)在教学中,应注重现代化教学手段的应用,可根据具体的教学内容和要求,采用板 书和多媒体课件相结合的教学方式,实施讲授法、启发引导式法、设疑讨论式法、案例教学 法、翻转课堂或微课等进行教学,加强教学互动,充分发挥教与学两个方面的积极性,保证 总体大纲的贯彻执行

《空间解析几何》课程课程教学大纲 (Analytic geometry) 执笔者:戎海武 审核人:黄国顺 编写日期:2017年9月 一、课程基本信息 适用专业 数学与应用数学 开课单位 数学与大数据学院 课程类型 专业教育类(专业基础课) 课程性质 必修课 是否为双语 否 学分数 3学分 学时数 总学时48 先修课程 后续课程 常微分方程,复变函数,实变函数,数理方程,数学建模 二、课程简介 解析几何的主要内容有矢量代数、轨迹与方程、平面与空间曲线、常用二次曲面、二次 曲线,它是几何学的一个分支,是近代几何的基础,它的许多概念和方法在代数、分析、力 学、物理等领域有着广泛的应用,也是每个数学专业的学生必须掌握的。随着科学技术的发 展,数学课程要不断改革,其中以几何课程的改革问题争议最多,难度最大,数学本是几何、 代数、分析有机地结合的整体,人们往往看重代数的、分析的方法,而容易忽略几何的观念, 其实,无论在数学史上还是在当代数学中,数学思想的飞跃和突破,常常是与几何学联系在 一起的。 解析几何是大学数学系的主要专业基础课之一,学好这一门课对于学习数学分析,高等 代数,微分几何等课程都有很大的帮助。 三、本课程所支撑的毕业要求 (本课程所支撑(达成)的毕业要求 39
39 《空间解析几何》课程课程教学大纲 (Analytic geometry) 执 笔 者:戎海武 审 核 人:黄国顺 编写日期:2017 年 9 月 一、课程基本信息 适用专业 数学与应用数学 开课单位 数学与大数据学院 课程类型 专业教育类 (专业基础课) 课程性质 必修课 是否为双语 否 学分数 3 学分 学时数 总学时 48 先修课程 后续课程 常微分方程,复变函数,实变函数,数理方程,数学建模 二、课程简介 解析几何的主要内容有矢量代数、轨迹与方程、平面与空间曲线、常用二次曲面、二次 曲线,它是几何学的一个分支,是近代几何的基础,它的许多概念和方法在代数、分析、力 学、物理等领域有着广泛的应用,也是每个数学专业的学生必须掌握的。随着科学技术的发 展,数学课程要不断改革,其中以几何课程的改革问题争议最多,难度最大,数学本是几何、 代数、分析有机地结合的整体,人们往往看重代数的、分析的方法,而容易忽略几何的观念, 其实,无论在数学史上还是在当代数学中,数学思想的飞跃和突破,常常是与几何学联系在 一起的。 解析几何是大学数学系的主要专业基础课之一,学好这一门课对于学习数学分析,高等 代数,微分几何等课程都有很大的帮助。 三、本课程所支撑的毕业要求 (本课程所支撑(达成)的毕业要求