
EA siay!uen = Kenb 台←L∧Vs3N1P3uu0) :…q‘D‘f‘x s31qeueΛ ··‘fO63If3T?bS suonoun ……‘<a叫0la saneoipald …‘aOn‘z‘uyor6uy squeisuo) squowal日pIs肥q:IOdJ0XeuS
ts elemen Basic OL: F of tax Syn . . . , BCU, 2 ohn, J ing K Constants . . . >, , other r B Predicates . . . , f O tLeg Lef t, rq S unctions F . . . b, a, , y x, riables aV ⇔ ⇒ ¬ ∨ ∧ Connectives = y Equalit ∃ ∀ Quantifiers 6 8 Chapter

&8md3 (((uyorbuy)fOb Tf T)ubuaT((pDy)fObTf T)ubuaT)< (qDayuoTay Ip.ior uyorbuy)3y01g3 ajqDiion io qungsuoo o (uu.la2‘.·[u.l3)u02pumf=uuBL tw.lag Iw.lag 1o ("w.iagIw.lag)anDopa.id aouaquas owoy seouaquas oiwo!y
tences sen tomic A )n m ter , . . . ,1 m ter ( edicate pr = sentence tomic A 2 m ter =1 m ter r o )n m ter , . . . , 1 m ter ( unction f = erm T e iabl ar v r o constant r o )t heLionhear dT ichar R ohn, J ing K( other r B E.g., ))) ohn J ing K( f O tLeg Lef ( th Leng , )) d ichar R( f O tLeg Lef ( th Leng ( > 7 8 Chapter

88 (亿)<LV(亿T)< (亿)5(亿‘)< (u40rbu2H‘plD4puH)6u1qS←(p.uo叫pH‘u40r6uH)6u1q2S:83 S台SS=ISS∧IS S VIS 'S sannpauuoo guisn saouaquas oiwone woyy apew aue seouequas xejdwo) soouaquas xeldwo
tences sen Complex connectives using sentences atomic from made re a sentences Complex 2 S ⇔1 S , 2 S ⇒1 S , 2 S ∨1 S , 2 S ∧1 S , S¬ ) ohn J ing Kd, ichar R( ing ibl S ⇒) d ichar R ohn, J ing K( ing ibl S E.g. 2) , (1 ≤∨ 2) , (1 > 2) , (1 >¬ ∧ 2) , (1 > 8 8 Chapter

68md0 agpoipa.id Kq o1 pajajal uonejal ay1 ul ale 4u.la1‘.…Tula4Kqo1p1sp3fqo叫4H an s!(ww.ian 'Iw.a)anDopa.d aouaquas olwone uy suonejal jeuonouny sjoqwks uonouny suonejasjoqwks aneoipad spafqo sjoqwks quensuo Joy squaajal sallpads uonenadJaqul wayn Suowe suoneja pue (squawaja ulewop)saoalqo I<suleuoo JepoW uonejadJalul ue pue japow e on adsal yim an ae saouanuas oI IopIo-sIy u yinIL
logic first-order in ruth T retation interp an and del mo a to ect resp with true re a Sentences them among relations and ) elements domain ( objects 1 ≥ contains del Mo r fo referents ecifies sp retation Interp objects → ols symb constant relations → ols symb redicate p relations functional → ols symb function true is )n m ter , . . . ,1 m ter ( edicate pr sentence atomic An n m ter , . . . , 1 m ter yb to referred objects the iff edicate pr yb to referred relation the in re a 9 8 Chapter
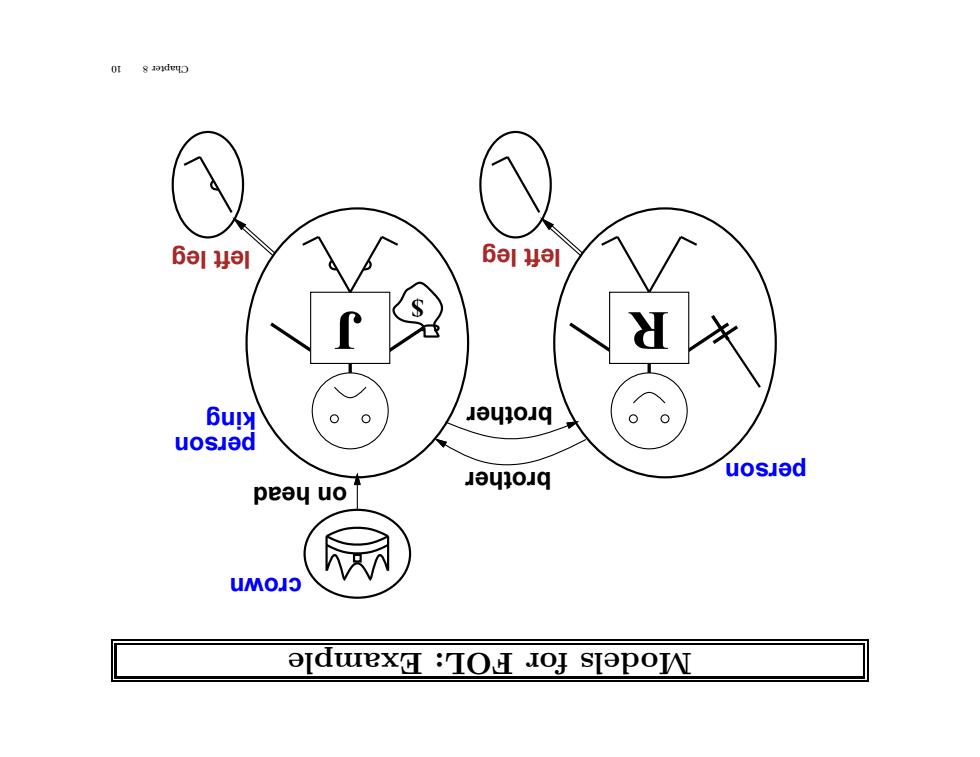
6a11 61 6ulx 0 1410q 00 uosled 叫10q uosJed peay uo UMO1O aldwexH :IOH IoJ SIOpoN
Example OL: F for dels Mo J $ R left leg left leg on head brother brother person person king crown 10 8 Chapter