
由式2)解得: WXH WXH 412yR3-u31yR2 RR+RR+RR i1A=u12aR12-431AR31 423YR1-12yR3 i2A=u23AR23-412A/R12广(I RR+RR3+RR (3) i3A=31AR31-423AR23 U31Y R2-4z3y R i3y RR+RR3+RR 根据等效条件,比较式(③)与式(1),得由Y接→△接的变换结果: R2=R+R2+ RR2 GG, R3 G12= G1+G2+G3 R23=R2+R3+ RR 或 G,G3 R G23= G1+G2+G3 R1=R3+R1+ RR G31= G:G1 R2 G+G2+G ☑
WXH WXH 21 1 2 2 3 3 1 12Y 3 31Y 2 1Y R R R R R R u R u R i 1 2 2 3 3 1 23Y 1 12Y 3 2Y R R R R R R u R u R i 1 2 2 3 3 1 31Y 2 23Y 1 3Y R R R R R R u R u R i 由式(2)解得: i3 =u31 /R31 – u23 /R23 i2 =u23 /R23 – u12 /R12 i1 =u12 /R12 – u31 /R31 (1) (3) 根据等效条件,比较式(3)与式(1),得由Y接接的变换结果: 2 3 1 31 3 1 1 2 3 23 2 3 3 1 2 12 1 2 R R R R R R R R R R R R R R R R R R 1 2 3 3 1 31 1 2 3 2 3 23 1 2 3 1 2 12 G G G G G G G G G G G G G G G G G G 或

WXH WXH 类似可得到由△接→Y接的变换结果: G=G2+G31+ G2G31 R R12R31 R12+R23+R31 G2=G23+G2+ G23G12 或 R23R12 G3 R2 R12+R23+R31 G3=G31+G23+ G:G23 R31R23 G R:=Rr+R+3 上述结果可从原始方程出发导出,也可由Y接→△接 的变换结果直接得到。 四区
WXH WXH 22 类似可得到由接 Y接的变换结果: 12 31 23 3 31 23 31 23 12 2 23 12 23 12 31 1 12 31 G G G G G G G G G G G G G G G G G G 12 23 31 31 23 3 12 23 31 23 12 2 12 23 31 12 31 1 R R R R R R R R R R R R R R R R R R 或 上述结果可从原始方程出发导出,也可由Y接 接 的变换结果直接得到

简记方法: WXH WXH Rr=△相邻电阻乘积 或 G =Y相邻电导乘积 ∑Ra ∑GY 特例:若三个电阻相等(对称),则有 R=3RY (外大内小) 注意: (1)等效对外部(端钮以外)有效,对内不成立。 (2)等效电路与外部电路无关。 ★
WXH WXH 23 简记方法: R R 相邻电阻乘积 特例:若三个电阻相等(对称),则有 R = 3RY ( 外大内小 ) 1 3 或 Y Y Δ G G 相邻电导乘积 注意: (1) 等效对外部(端钮以外)有效,对内不成立。 (2) 等效电路与外部电路无关

例如图所示,求桥形申路的总电阻R2 WXH ① 解: ① 0.82 ③ .4Ω 2 ⑤ 方法二 22 ② 4S2 22 →82 2.6842 12 ⑤ ②o
WXH WXH 24 例 如图所示,求桥形电路的总电阻R12。 R12 2Ω 2Ω 2Ω 1Ω 1Ω 1Ω ① ② ④ ③ ⑤ 解: R12 0.4Ω 0.4Ω 2Ω 0.8Ω 1Ω 1Ω ① ② ④ ③ ⑤ R12 0.4Ω 0.4Ω 2Ω 0.8Ω 1Ω 1Ω ① ② ④ ③ ⑤ ① ② R12 2.684Ω R12 8Ω 2Ω 1Ω 4Ω 4Ω 1Ω ① ② ④ ⑤ 方法一 方法二
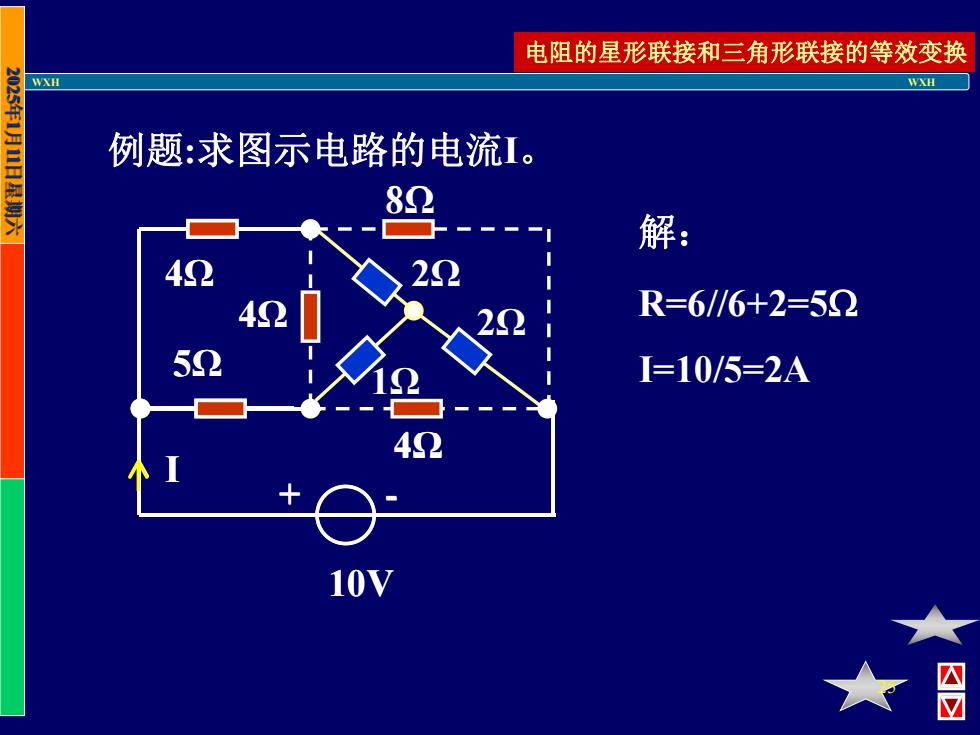
电阻的星形联接和三角形联接的等效变换 WXH WXH 例题:求图示电路的电流I。 解: 42 42 R=6/6+2=52 52 I=10/5=2A 10V
WXH WXH 25 例题:求图示电路的电流I。 解: R=6//6+2=5 I=10/5=2A I 10V + - 4Ω 5Ω 4Ω 4Ω 8Ω 电阻的星形联接和三角形联接的等效变换 I 10V + - 4Ω 5Ω 4Ω 4Ω 8Ω 2Ω 1Ω 2Ω