WXH 求:11,14,U4 2i12方2R12 解: ①用分流方法做 2=-3 8 2R U4=-I4×2R=3V =号 ②用分压方法做 U2=1U1=3V 4 14=- 3 2R ★
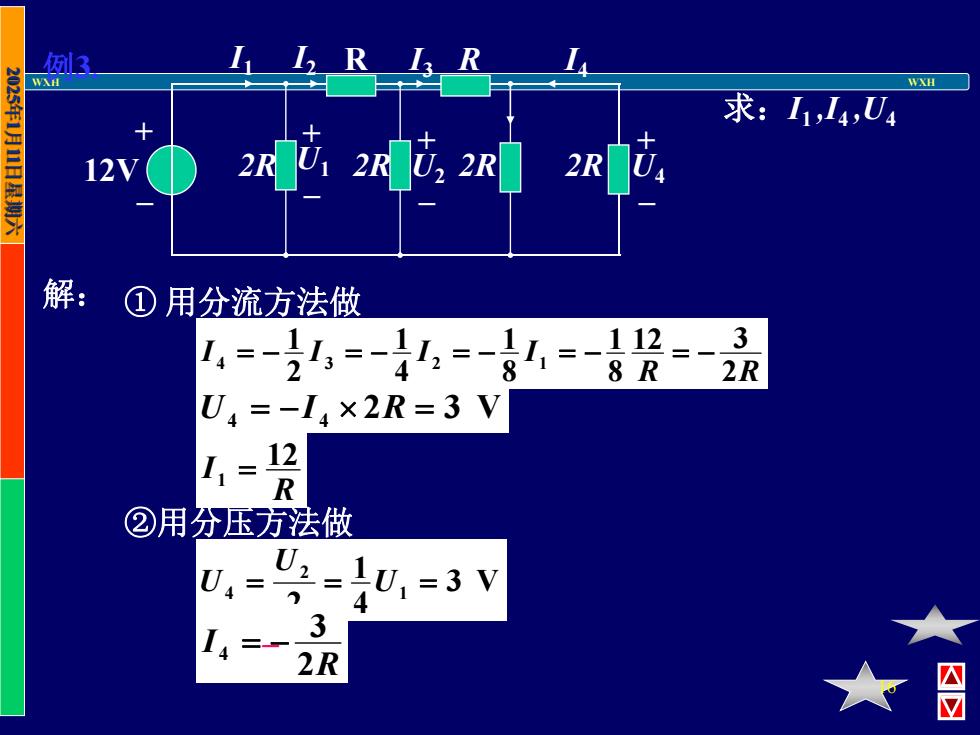
WXH WXH 16 例3. 解: ① 用分流方法做 ②用分压方法做 R R I I I I 2 12 3 8 1 8 1 4 1 2 1 4 3 2 1 3 V 4 1 2 1 2 4 U U U R I 12 1 U4 I 4 2R 3 V R I 2 3 4 求:I1 ,I4 ,U4 + _ 2R 2R 2R 2R I1 I2 R I3 R I4 12V + _U4 + _U2 + _U1 _

X田 WXH 教材第32页,例2.1.2 注意结论的实用性。 第33页,练习与思考
WXH WXH 17 教材第32页,例2.1.2 注意结论的实用性。 第33页,练习与思考
*§2-2电阻的星形联接和三角形联接的等效变换 WXH WXH 2025111 R31 3 R23 (a)三角形联接 (b)星形联接 如果要使两个内部结构不同两个 网络等效,则其端口上的伏安关系完 全相同。如上图所示
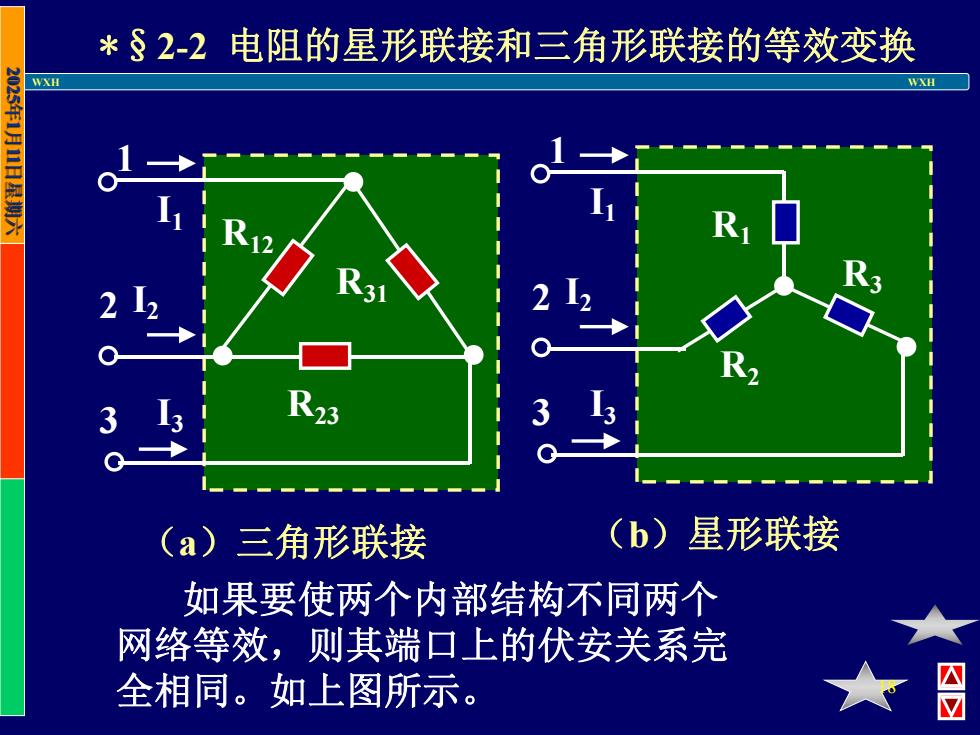
WXH WXH 18 *§2-2 电阻的星形联接和三角形联接的等效变换 I1 I2 I3 R23 R12 R31 1 2 3 I1 I2 I3 R2 R1 R3 1 2 3 如果要使两个内部结构不同两个 网络等效,则其端口上的伏安关系完 全相同。如上图所示。 (a)三角形联接 (b)星形联接
下面是△,Y网络的变形: WXH WXH 元型电路(公型) T型电路Y型) 这两种电路都可以用下面的△-Y变换方法来做。 下面要证明:这两个电路当它们的电阻满足一定的关系时, 是能够相互等效的。 等效的条件 i1△=i1Y,i2A=i2Y,3△-3y) 且 U12A=412Y,u23△=23Y,431△=u31Y 囚
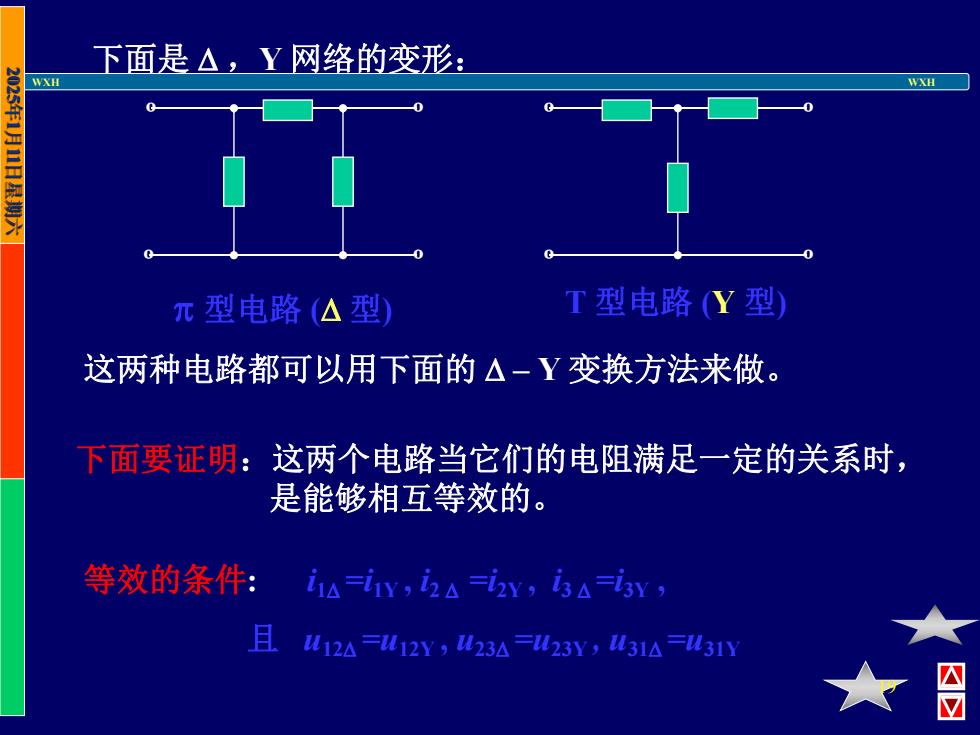
WXH WXH 19 下面是 ,Y 网络的变形: º º º º º º º º 型电路 ( 型) T 型电路 (Y 型) 这两种电路都可以用下面的 – Y 变换方法来做。 下面要证明:这两个电路当它们的电阻满足一定的关系时, 是能够相互等效的。 等效的条件: i1 =i1Y , i2 =i2Y , i3 =i3Y , 且 u12 =u12Y , u23 =u23Y , u31 =u31Y
WXH WXH 12△ W31A R12 01 12 K23 t236 4231 △接:用电压表示电流 Y接:用电流表示电压 iA=u12AR12-l31△R31 U12Y=RiIY-R2iY i2A=423A/R23-412A/R12广(1) 423Y=Rzizy-R3i3Y iA=u31a/R31-423A/R23 u31y=R3isy-RiiY iy+izy+isy=0 ★ 囹
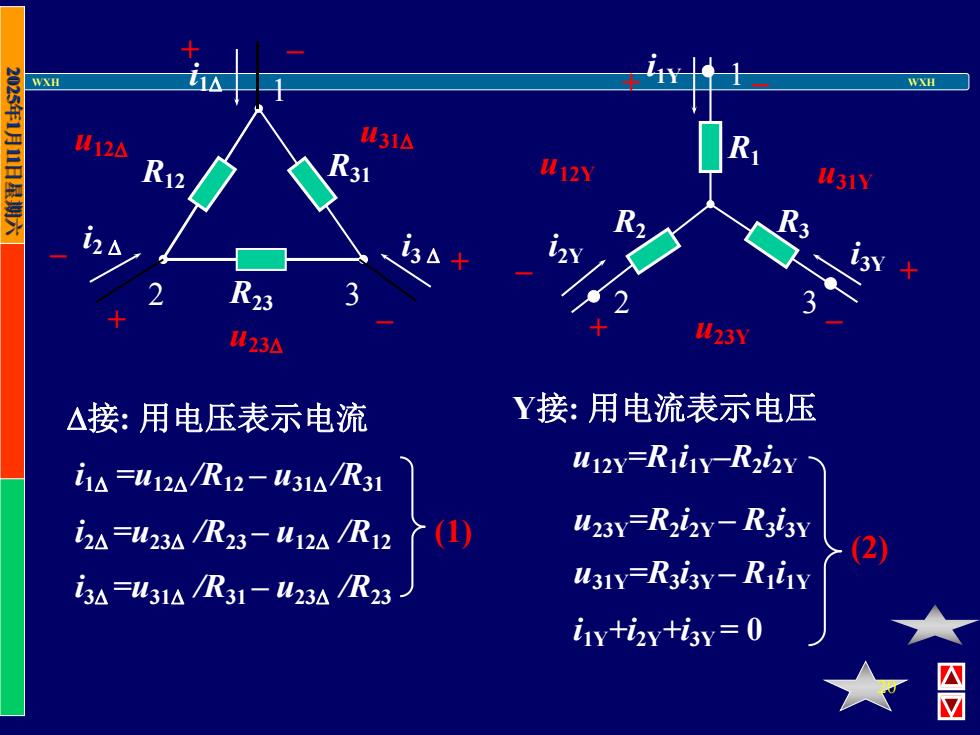
WXH WXH 20 Y接: 用电流表示电压 u12Y=R1 i1Y–R2 i2Y 接: 用电压表示电流 i1Y+i2Y+i3Y = 0 u31Y=R3 i3Y – R1 i1Y u23Y=R2 i2Y – R3 i3Y i3 =u31 /R31 – u23 /R23 i2 =u23 /R23 – u12 /R12 R12 R31 R23 i3 i2 i1 1 2 3 + + + – – – u12 u23 u31 R1 R2 R3 i1Y i2Y i3Y 1 2 3 + + – + – – u12Y u23Y u31Y i1 =u12 /R12 – u31 /R31 (1) (2)