
第2章液压流体力学基础 妆 已.2浪体静力学 2.2.1 静压力及其特性只 2.2.2静压力基本方程式 2.2.3 帕斯卡原理 2.2.4静压力对固体壁面的作用力只 11 本章主页 本章目录 上一页 下一页后退退出
第2章 液压流体力学基础 11 2.2.1 静压力及其特性 2.2.2 静压力基本方程式 2.2.3 帕斯卡原理 2.2.4 静压力对固体壁面的作用力 2.2 液体静力学

第2章 液压流体力学基础 2.2.1静压力及其特性 1.液体的静压力 液体静压力在物理学上称为压强,在工程实际应用中习惯上 称为压力。 2.液体静压力的特性 (1)液体静压力垂直于其承压面,其方向和该面的内法线方向 致。 (2)静止液体内任一点所受到的静压力在各个方向上都相等。 12 本章主页本章目录 上一页 下一页 后退 退出
第2章 液压流体力学基础 12 1. 液体的静压力 液体静压力在物理学上称为压强,在工程实际应用中习惯上 称为压力。 2. 液体静压力的特性 (1) 液体静压力垂直于其承压面,其方向和该面的内法线方向 一致。 (2) 静止液体内任一点所受到的静压力在各个方向上都相等。 2.2.1 静压力及其特性
第2章液压流体力学基础 2.2.2静压力基本方程式 1.静压力基本方程式 在重力作用下的静止液体所受的力,其受力情况如图2-4a所示。 由于液柱受力平衡,故 p△M4=PAA+Pgh△4 (2-9) a) b) 图2-4静止液体内压力分布规律 将式(2-9)两边同除以△4,则得静压力基本方程式 p-Po+pgh (2-10) 13 本章主页 本章目录 上一页 下一页 后退 退出
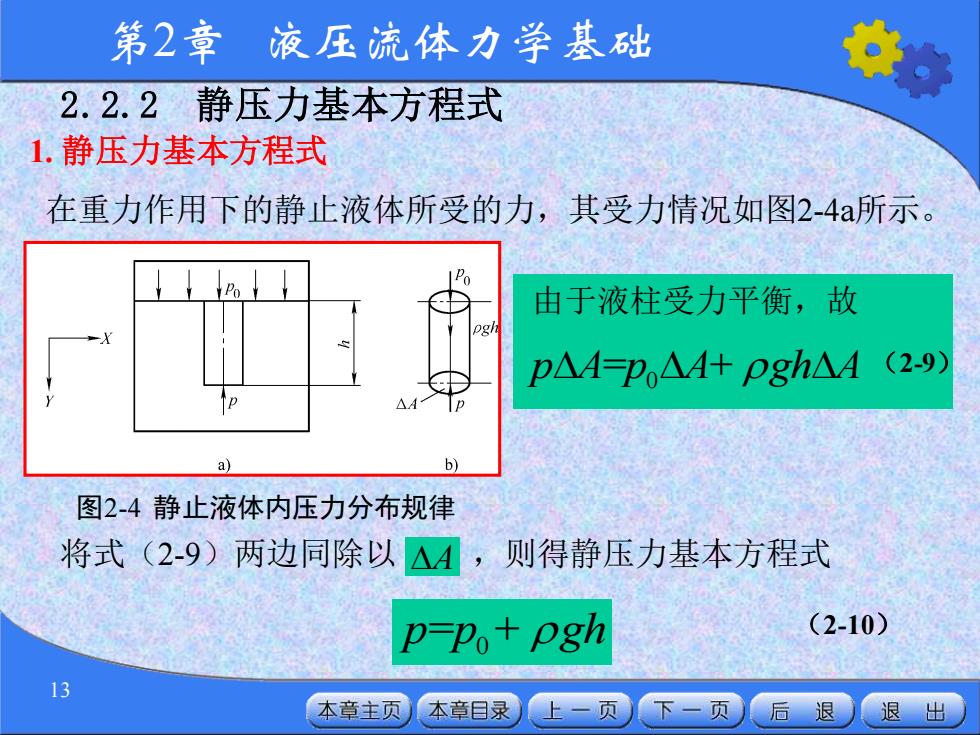
第2章 液压流体力学基础 13 由于液柱受力平衡,故 2.2.2 静压力基本方程式 1. 静压力基本方程式 在重力作用下的静止液体所受的力,其受力情况如图2-4a所示。 图2-4 静止液体内压力分布规律 = + 0 p A p A gh A (2-9) 将式(2-9)两边同除以 ,则得静压力基本方程式 = + 0 p p gh (2-10) A

第2章 液压流体力学基础 由上式可知:重力作用下的液体其压力分布具有如下的 特征: (1)静止液体内任一点处的压力由两部分组成: p=Pa+pgh (2-11) (2)静止液体内压力随液体深度呈直线规律递增。 (3)离液面深度相同处各点的压力均相等,而压力相等的所有点 组成的面叫做等压面。 (4)能量守恒。 P+hn=卫+h=常量 (2-12) pg 式中,P0/g为静止液体中单位质量液体的压力能,h为单位质量液体的势能。 14 本章主页 本章目录 上一页 下一页 后退 退出
第2章 液压流体力学基础 14 (1) 静止液体内任一点处的压力由两部分组成: 由上式可知:重力作用下的液体其压力分布具有如下的 特征: (2) 静止液体内压力随液体深度呈直线规律递增。 (3) 离液面深度相同处各点的压力均相等,而压力相等的所有点 组成的面叫做等压面。 (4) 能量守恒。 + = + h = 常量 g p h g p 0 0 (2-11) (2-12) p = pa + gh 式中,p0/g为静止液体中单位质量液体的压力能,h为单位质量液体的势能

第2章 液压流体力学基础 2.压力的表示方法及单位 (1)绝对压力。 (2)相对压力(表压力):用压力表测得的压力数值是相对压力。 (3)真空度。 压力的单位以及各种表示法之间的换算关系如下: 1Pa(帕)=1N/m2;1bar(巴)=1×105Pa=1×105N/m2, 1at(工程大气压)=1 kgf/cm2=9.8×104N/m2;,1mH0(米水柱)= 9.8×103N/m2, 1mmHg(毫米汞柱)=1.33×102N/m2 绝对压力、相对压力和真空度的关系见图25(下页) 15 本章主页 本章目录 上一页 下一页 后退 退出
第2章 液压流体力学基础 15 2. 压力的表示方法及单位 (1)绝对压力。 (2)相对压力(表压力):用压力表测得的压力数值是相对压力。 (3)真空度。 1Pa(帕)=1 N/m2;1bar(巴)=1×105 Pa=1×105 N/m2 ; 1at(工程大气压)=1kgf/cm2=9.8×104 N/m2 ; 1mH2O(米水柱)= 9.8×103 N/m2 ; 1mmHg (毫米汞柱)=1.33×102 N/m2 。 绝对压力、相对压力和真空度的关系见图2-5(下页)。 压力的单位以及各种表示法之间的换算关系如下: