
第一章复数与复变函数 历安毛子代枚大等 XIDIAN UNIVERSITY Complex number and complex variable functions 附:人物介绍一高斯 。高斯去世后,哥廷根大学对高斯的文稿进行了整理, 历时67年,出版了《高斯全集》,共12卷。 。在哥廷根大学的广场上,矗立着一座用白色大理石砌 成的纪念碑,它的底座砌成正十七边形,纪念碑上是 高斯的青铜雕像。 场论与复变函数Field Theory and Complex Variable Functions 19
场论与复变函数 Field Theory and Complex Variable Functions 19 第一章 复数与复变函数 Complex number and complex variable functions 高斯去世后,哥廷根大学对高斯的文稿进行了整理, 历时67年,出版了《高斯全集》,共12卷。 在哥廷根大学的广场上,矗立着一座用白色大理石砌 成的纪念碑,它的底座砌成 正十七边形,纪念碑上是 高斯的青铜雕像。 附:人物介绍 —— 高斯

第一章复数与复变函数 历安毛子代枚大” XIDIAN UNIVERSITY Complex number and complex variable functions 第二节 复数的几何表示 一、复数的几种表示方法 二、曲线的复数方程 场论与复变函数Field Theory and Complex Variable Functions 20
场论与复变函数 Field Theory and Complex Variable Functions 20 第一章 复数与复变函数 Complex number and complex variable functions 第二节 复数的几何表示 一、复数的几种表示方法 二、曲线的复数方程

历安毛子代枝大学 第一章复数与复变函数 XIDIAN UNIVERSITY Complex number and complex variable functions 复数的几种表示方法 1.1复平面 定义在平面上建立一个直角坐标系,用坐标为(x,y)的点来 表示复数z=x+y,从而将全体复数和平面上的全部点 对应起来,这样表示复数z的平面称为复平面或者 z平面。 此时,x轴称为实轴,y轴称为虚轴。 y轴 虚轴 (x,) =x+vi x轴 实轴 场论与复变函数Field Theory and Complex Variable Functions 21
场论与复变函数 Field Theory and Complex Variable Functions 21 第一章 复数与复变函数 Complex number and complex variable functions 一、复数的几种表示方法 此时,x 轴称为实轴,y 轴称为虚轴。 定义 在平面上建立一个直角坐标系,用坐标为 (x , y) 的点来 表示复数 z x i y , 从而将全体复数和平面上的全部点 一一对应起来,这样表示复数 z 的平面称为复平面或者 z 平面。 1.1 复平面
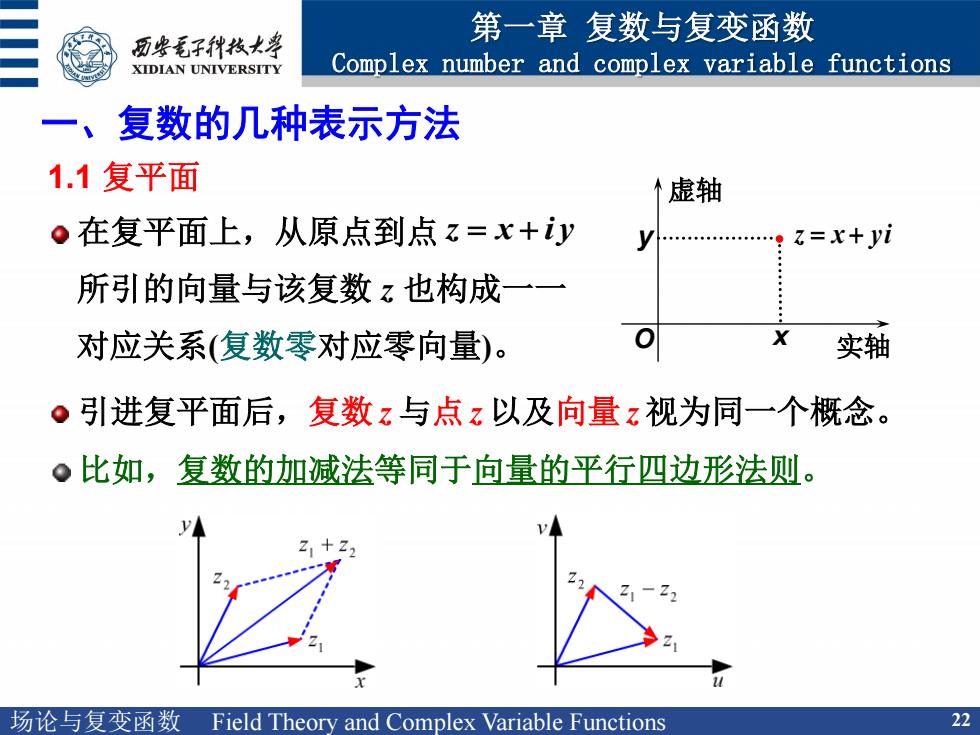
第一章复数与复变函数 历华毛子代枝七 XIDIAN UNIVERSITY Complex number and complex variable functions 复数的几种表示方法 1.1复平面 个虚轴 。在复平面上,从原点到点z=x+y z=x+yi 所引的向量与该复数z也构成一一 对应关系(复数零对应零向量)。 实轴 。引进复平面后,复数z与点z以及向量z视为同一个概念。 。比如,复数的加减法等同于向量的平行四边形法则。 场论与复变函数Field Theory and Complex Variable Functions 22
场论与复变函数 Field Theory and Complex Variable Functions 22 第一章 复数与复变函数 Complex number and complex variable functions 引进复平面后,复数 z 与点 z 以及向量 z 视为同一个概念。 在复平面上,从原点到点 z x i y 所引的向量与该复数 z 也构成一一 y 实轴 虚轴 z x yi 对应关系 O x (复数零对应零向量)。 比如,复数的加减法等同于向量的平行四边形法则。 一、复数的几种表示方法 1.1 复平面

第一章复数与复变函数 历坐毛子代枚七学 XIDIAN UNIVERSITY Complex number and complex variable functions 复数的几种表示方法 1.1复平面 。将复数和向量对应之后,除了利用实部 P 与虚部来给定一个复数以外,还可以借 t=x+yi 助向量的长度与方向来给定一个复数。 X X 定义设z是一个不为0的复数, (1)向量z的长度r称为复数z的模,记为|z (2)向量z的“方向角”0称为复数z的辐角,记为Agz. 模:lz=OP=r=Vx2+y2, 记作 辐角:0=Argz 场论与复变函数 Field Theory and Complex Variable Functions 23
场论与复变函数 Field Theory and Complex Variable Functions 23 第一章 复数与复变函数 Complex number and complex variable functions 将复数和向量对应之后,除了利用实部 与虚部来给定一个复数以外,还可以借 y z x yi O x x y r 定义 设 z 是一个不为 0 的复数, (1) 向量 z的长度 r 称为复数 z 的模,记为 |z|. 助向量的长度与方向来给定一个复数。 (2) 向量 z的“方向角” 称为复数 z的辐角,记为 Arg z. z z OP r x y : Arg | | | | , 2 2 记 作 辐 角 模 : P 一、复数的几种表示方法 1.1 复平面