
第11章内压薄壁容器的应力分析本章重点:薄膜理论的应用本章难点:满薄膜理论学时:6学时工程实际中,应用较多的是薄壁容器,并且,这些容器的几何形状常常是轴对称的,而且所受到的介质压力也常常是轴对称的,甚至于它的支座,或者说约束条件都对称于回转轴我们把几何形状、所受外力、约束条件都对称于回转轴的问题称为轴对称问题。5返回回主目录一上一内容下一内容2025/6/10
上一内容 下一内容 回主目录 返回 2025/6/10 本章重点:薄膜理论的应用 本章难点:薄膜理论 学 时:6学时 工程实际中,应用较多的是薄壁容器,并 且,这些容器的几何形状常常是轴对称的,而 且所受到的介质压力也常常是轴对称的,甚至 于它的支座,或者说约束条件都对称于回转轴, 我们把几何形状、所受外力、约束条件都对称 于回转轴的问题称为轴对称问题。 第11章 内压薄壁容器的应力分析

第一节薄膜应力理论回转壳体中的几个重要的几何概念(一)面1、中间面:平分壳体厚度的曲面称为壳体的中间面,中间面与壳体内外表面等距离,它代表了壳体的几何特性回转曲面:由平面直线或平面曲线绕21其同平面内的回转轴回转一周所形成的曲面。3、回转壳体:由回转曲面作中间面形成的壳体称为回转壳体。5返回上一内容下一内容口主目录2025/6/10
上一内容 下一内容 回主目录 返回 2025/6/10 一、回转壳体中的几个重要的几何概念 (一)面 1、中间面:平分壳体厚度的曲面称为壳 体的中间面,中间面与壳体内外表面等 距离,它代表了壳体的几何特性。 2、回转曲面:由平面直线或平面曲线绕 其同平面内的回转轴回转一周所形成的 曲面。 3、回转壳体:由回转曲面作中间面形成 的壳体称为回转壳体。 第一节 薄膜应力理论

第一节薄膜应力理论(二)线1、母线:绕回转轴回转形成中间面的平面曲线。2、经线:过回转轴的平面与中间面的交线。3、法线:过中间面上的点且垂直于中间面的直线称为中间面在该点的法线(法线的延长线必与回转轴相交)4、纬线:以法线为母线绕回转轴回转一周所形成的圆锥法截面与中间面的交线。5、平行圆:垂直于回转轴的平面与中间面的交线称平行圆。显然,平行圆即纬线。5返回回主目录←上一内容下一内容2025/6/10
上一内容 下一内容 回主目录 返回 2025/6/10 (二)线 1、母线:绕回转轴回转形成中间面的平面曲线。 2、经线:过回转轴的平面与中间面的交线。 3、法线:过中间面上的点且垂直于中间面的直 线称为中间面在该点的法线(法线的延长线必 与回转轴相交)。 4、纬线:以法线为母线绕回转轴回转一周所形 成的圆锥法截面与中间面的交线。 5、平行圆:垂直于回转轴的平面与中间面的交 线称平行圆。显然,平行圆即纬线。 第一节 薄膜应力理论

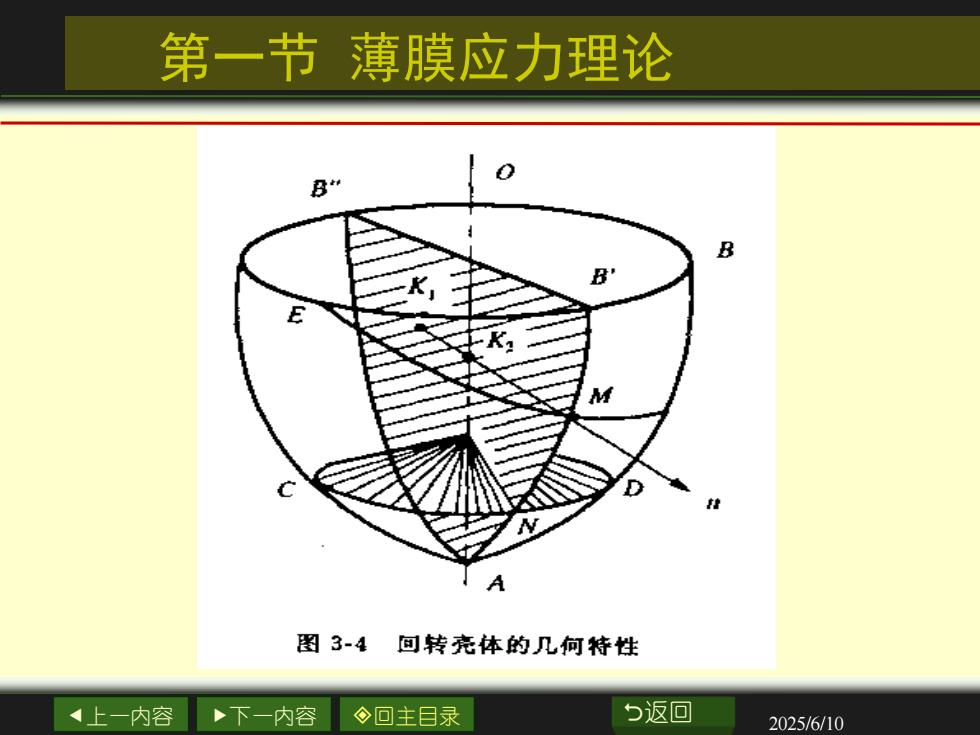
第一节薄膜应力理论(三)、半径1、第一曲率半径:中间面上任一点M处经线的曲率半径为该点的“第一曲率半径”R1,R,=MK1。S数学公式:(1 + y/2)2RV2、第二曲率半径:通过经线上一点M的法线作垂直于经线的平面与中间面相割形成的曲线MEF,此曲线在M点处的曲率半径称为该点的第二曲率半径R2。第二曲率半径的中心落在回转轴上,其长度等于法线段MK2,即R2=MK2。5返回上一内容下一内容口主目录2025/6/10
上一内容 下一内容 回主目录 返回 2025/6/10 (三)、半径 1、第一曲率半径:中间面上任一点M处经线的曲率半 径为该点的“第一曲率半径”R1,R1=MK1。 数学公式: 3 / 2 2 1 // (1 ) | | y R y + = 2、第二曲率半径:通过经线上一点M的法线作垂直于 经线的平面与中间面相割形成的曲线MEF,此曲线在 M点处的曲率半径称为该点的第二曲率半径R2。第二 曲率半径的中心落在回转轴上,其长度等于法线段 MK2,即R2=MK2。 第一节 薄膜应力理论
第一节薄膜应力理论0B"RB'K.EMA图3-4回转亮体的几何特性5返回上一内容下一内容今回主日录2025/6/10
上一内容 下一内容 回主目录 返回 2025/6/10 第一节 薄膜应力理论