
第一节薄膜应力理论、薄壁容器及其应力特点1、薄壁容器容器的厚度与其最大截面圆的内径之比小于0.1即S/D<0.1亦即K=D/D:≤1.2(D.为容器的外径,D,为容器的内径,S为容器的厚度)的容器称为薄壁容器2、应力特点在任何一个压力容器中,总是存在两类不同性质的应力:薄膜应力-一可用简单的无力矩理论计算-边缘应力一要用比较复杂的有力矩理论和变形协调条件才能计算。5返回上一内容下一内容回主目录2025/6/10
上一内容 下一内容 回主目录 返回 2025/6/10 二、薄壁容器及其应力特点 1、薄壁容器 容器的厚度与其最大截面圆的内径之比小于0.1, 即S/Di<0.1亦即K=Do/Di≤1.2(Do为容器的外径,Di为 容器的内径,S为容器的厚度)的容器称为薄壁容器。 2、应力特点 在任何一个压力容器中,总是存在两类不同性质 的应力: 薄膜应力——可用简单的无力矩理论计算 边缘应力——要用比较复杂的有力矩理论和变形 协调条件才能计算。 第一节 薄膜应力理论
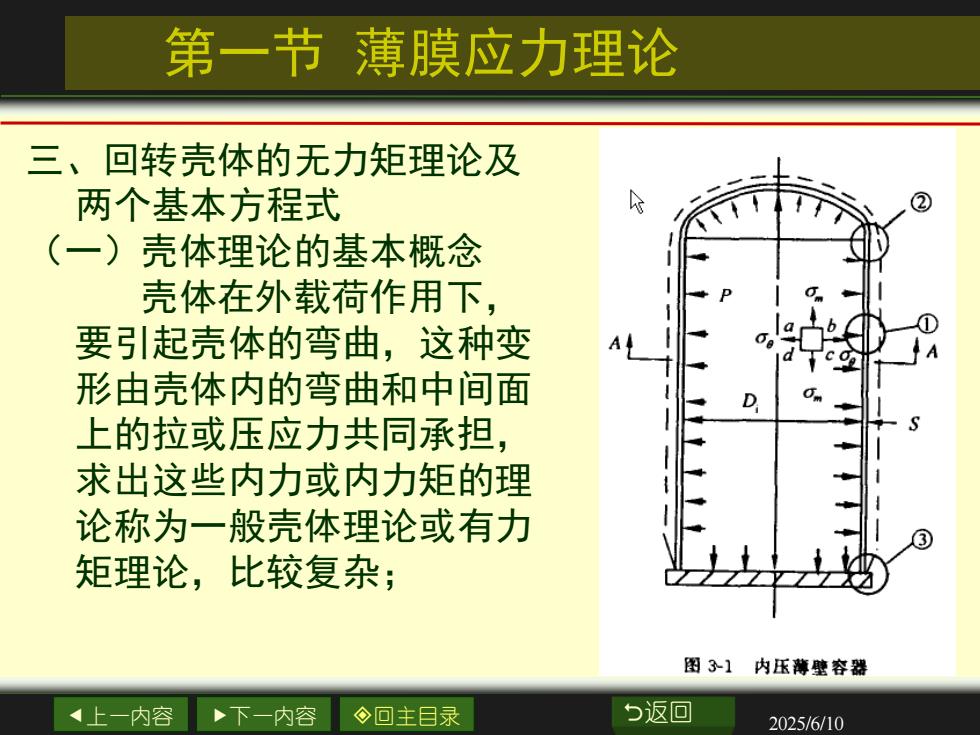
第一节薄膜应力理论三、回转壳体的无力矩理论及A②两个基本方程式(一)壳体理论的基本概念Om壳体在外载荷作用下Palab要引起壳体的弯曲,这种变ALTATco形由壳体内的弯曲和中间面amD.上的拉或压应力共同承担-求出这些内力或内力矩的理论称为一般壳体理论或有力?矩理论,比较复杂;图3-1内压薄壁容器5返回今回主目录上一内容下一内容2025/6/10
上一内容 下一内容 回主目录 返回 2025/6/10 三、回转壳体的无力矩理论及 两个基本方程式 (一)壳体理论的基本概念 壳体在外载荷作用下, 要引起壳体的弯曲,这种变 形由壳体内的弯曲和中间面 上的拉或压应力共同承担, 求出这些内力或内力矩的理 论称为一般壳体理论或有力 矩理论,比较复杂; 第一节 薄膜应力理论
第一节薄膜应力理论但是,对于壳体很薄,壳体具有连续的几何曲面,所受外载荷连续,边界支承是自由的,壳体内的弯曲应力与中间面的拉或压应力相比,中到可以忽略不计,认为壳体的外载荷只是由中间面的应力来平衡,这种处理方法,称为薄膜理论或无力矩理论。1、有力矩理论2、无力矩理论(应用无力矩理论,要假定壳体完全弹性,材料具有连续性、均匀性各各向同性,此外,对于薄壁壳体,通常采用以下三点假设使问题简化)1)小位移假设2)直法线假设3)不挤压假设5返回上一内容下一内容回主日录2025/6/10
上一内容 下一内容 回主目录 返回 2025/6/10 但是,对于壳体很薄,壳体具有连续的几何曲面,所 受外载荷连续,边界支承是自由的,壳体内的弯曲应 力与中间面的拉或压应力相比,中到可以忽略不计, 认为壳体的外载荷只是由中间面的应力来平衡,这种 处理方法,称为薄膜理论或无力矩理论。 1、有力矩理论 2、无力矩理论(应用无力矩理论,要假定壳体完全弹 性,材料具有连续性、均匀性各各向同性,此外,对 于薄壁壳体,通常采用以下三点假设使问题简化) 1)小位移假设 2)直法线假设 3)不挤压假设 第一节 薄膜应力理论

第一节氵薄膜应力理论(二)、回转壳体应力分析及基本方程式1、区域平衡方程式用截载面法将壳体沿经线的法线方向切开,即在平行园直径D处有垂直于经线的法向圆锥面截开,取下部作脱离体,建立静力平衡方程式RDS图3-6回转充体的经向应力分析5返回今回主目录←上一内容一下一内容2025/6/10
上一内容 下一内容 回主目录 返回 2025/6/10 (二)、回转壳体应力分析及基本方程式 1、区域平衡方程式 用截面法将壳体沿经线的法线方向切开,即在平 行园直径D处有垂直于经线的法向圆锥面截开,取下 部作脱离体,建立静力平衡方程式 。 第一节 薄膜应力理论
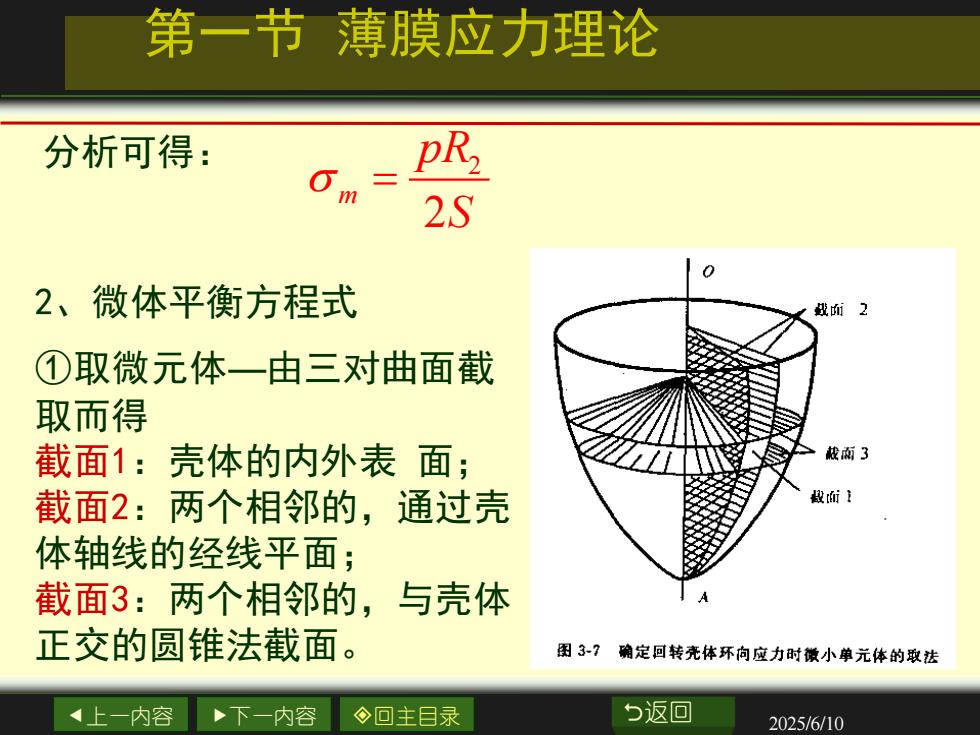
第一节薄膜应力理论pR分析可得:Om2S2、微体平衡方程式峨面2①取微元体一由三对曲面截取而得载两3图截面1:壳体的内外表面;载而!截面2:两个相邻的,通过壳体轴线的经线平面;截面3:两个相邻的,与壳体A正交的圆锥法截面。图3-?确定回转壳体环向应力时微小单元体的取法5返回1上一内容下一内容回主目录2025/6/10
上一内容 下一内容 回主目录 返回 2025/6/10 分析可得: 2 2 m pR S = 2、微体平衡方程式 ①取微元体—由三对曲面截 取而得 截面1:壳体的内外表 面; 截面2:两个相邻的,通过壳 体轴线的经线平面; 截面3:两个相邻的,与壳体 正交的圆锥法截面。 第一节 薄膜应力理论