
二、假设测验的步骤 如上述小麦新品种例, 0g5) 0=300,0x=15, 1.96o=29.4(kg)。因之, 0.02 它的两个2.5%概率 的否定区域为 0.01 接受区域 否定区域 否定区域 x≤300-29.4和 2.5% 2.5% x≥300+29.4,即 0.001 255 270 285 300 315 30 345 大于329.4(kg)和小于 270.6 329.4 270.6(kg)的概率只有5%。 图 5%显著水平假设测验图示 (表示接受区域和否定区域)
255 270 285 300 315 330 345 0.00 0.01 0.02 0.03 f N (y) y 270.6 329.4 否定区 域 2.5% 否定区 域 2.5% 接 受 区 域 平均数取值 如上述小麦新品种例, =300, , 1.96 =29.4(kg)。因之, 它的两个2.5%概率 的否定区域为 ≤300-29.4和 ≥300+29.4,即 大于329.4(kg)和小于 270.6(kg)的概率只有5%。 0 x 15 x = x x 图 5%显著水平假设测验图示 (表示接受区域和否定区域) 二、假设测验的步骤

二、假设测验的步骤 (三)根据“小概率事件实际上不可能发生”原理接受或否定假设 当下-4由随机误差造成的概率P小于5%或1%时,就 可认为它不可能属于抽样误差,从而否定假设。 如P<0.05,则称这个差数是显著的。 如P<0.01,则称这个差数是极显著的。 用来测验假设的概率标准5%或1%等,称为显著水平 (significancelevel)。一般以ax表示,如a=0.05或=0.01
(三) 根据“小概率事件实际上不可能发生”原理接受或否定假设 当 由随机误差造成的概率P小于5%或1%时,就 可认为它不可能属于抽样误差,从而否定假设。 如P<0.05,则称这个差数是显著的。 如P<0.01,则称这个差数是极显著的。 用来测验假设的概率标准5%或1%等,称为显著水平 ( significance level )。 一般以 表示,如 =0.05或 =0.01。 x − 二、假设测验的步骤

二、假设测验的步骤 综合上述,统计假设测验的步骤可总结如下: (1)对样本所属的总体提出统计假设,包括无效假设和备 择假设。 (2)规定测验的显著水平a值。 (3)在H为正确的假定下,根据平均数(x)或其他统计数 的抽样分布,获得实际差数(如下一4等)由误差造成的概 率(P值)。或者根据已规定概率,如=0.05,划出两个否定区 域如丽≤4-1.96o元和≥4+1.96o元。 (4)将规定的值和算得的P值相比较,或者将试验结果 和否定区域相比较,从而作出接受或否定无效假设的推断
综合上述,统计假设测验的步骤可总结如下: (1) 对样本所属的总体提出统计假设,包括无效假设和备 择假设。 (2) 规定测验的显著水平 值。 (3) 在 为正确的假定下,根据平均数( )或其他统计数 的抽样分布,获得实际差数(如 等)由误差造成的概 率(P值)。或者根据已规定概率,如 =0.05,划出两个否定区 域如: 和 。 (4) 将规定的 值和算得的P值相比较,或者将试验结果 和否定区域相比较,从而作出接受或否定无效假设的推断。 H0 x 1.96 x x − 1.96 x x + x − 二、假设测验的步骤

三、两尾测验与一尾测验 如果统计假设为Ho:山=4,则备择假设为H4:4≠4,在 假设测验时所考虑的概率为曲线左边一尾概率和右边一尾概率 的总和。这类测验称为两尾测验(two-tailed test),它具有两个 否定区域。 如果统计假设为H。:山≤4,则其对应的备择假设必 为H4:4>山,。因而,这个对应的备择假设仅有一种可能性, 而统计假设仅有一个否定区域,即曲线的右边一尾。这类测 验称一尾测验(one-tailed test)。一尾测验还有另一种情况, 即H。:H≥4,H4:4<4,这时否定区域在左边一尾
如果统计假设为 , 则备择假设为 , 在 假设测验时所考虑的概率为曲线左边一尾概率和右边一尾概率 的总和。这类测验称为两尾测验( two-tailed test ),它具有两个 否定区域。 0 0 H : = 0 HA : 如果统计假设为 , 则其对应的备择假设必 为 。因而,这个对应的备择假设仅有一种可能性, 而统计假设仅有一个否定区域,即曲线的右边一尾。这类测 验称一尾测验( one-tailed test )。一尾测验还有另一种情况, 即 , , 这时否定区域在左边一尾. 0 0 H : 0 HA : 0 0 H : 0 HA : 三、两尾测验与一尾测验
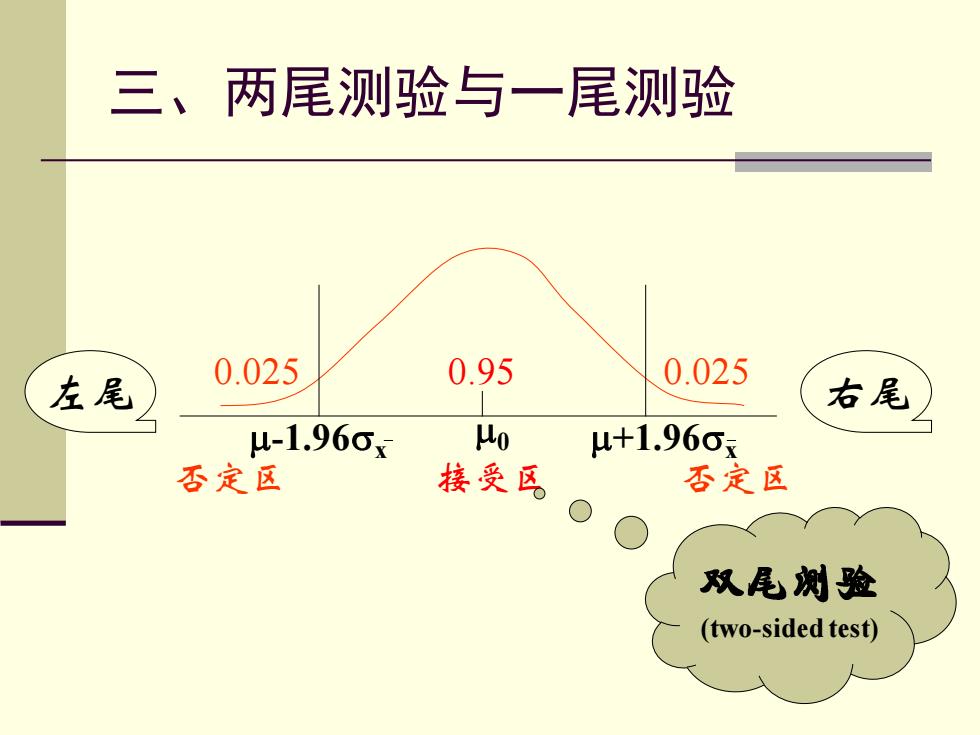
三、两尾测验与一尾测验 左尾 0.025 0.95 0.025 右尾 u-1.96ox 40 u+1.96ox 否定区 接受区 否定区 双尾树验 (two-sided test)
-1.96 0 x +1.96x 0.025 0.95 0.025 左尾 右尾 否定区 接受区 否定区 (two-sided test) 三、两尾测验与一尾测验