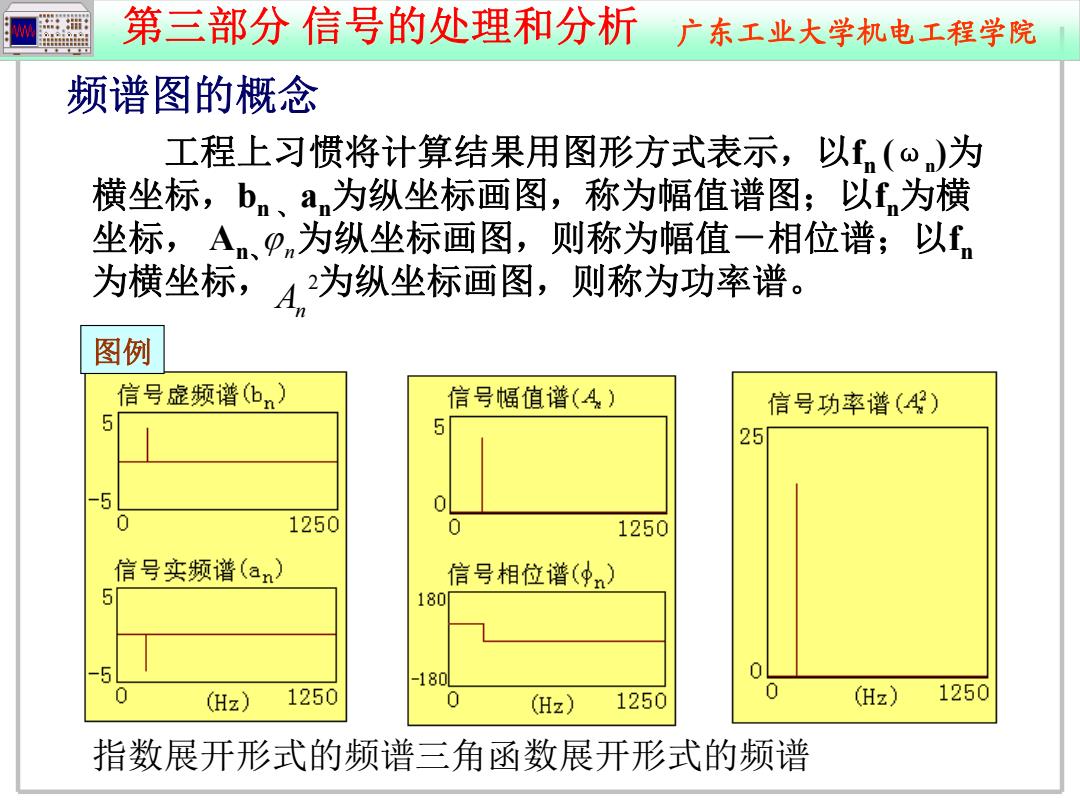
第三部分信号的处理和分析广东工业大学机电工程学院 频谱图的概念 工程上习惯将计算结果用图形方式表示,以£(o)为 横坐标,bn、an为纵坐标画图,称为幅值谱图;以fn为横 坐标,A、pn为纵坐标画图,则称为幅值一相位谱;以f。 为横坐标,4,为纵坐标画图,则称为功率谱。 图例 信号虚频谱(bn) 信号幅值谱(A) 信号功率谱(4好) 5 5 25 -5 0 1250 0 1250 信号实频谱(arn) 信号相位谱(9n) 5 180 -180 0 0 (Hz) 1250 0 (Hz) 1250 0 (Hz) 1250 指数展开形式的频谱三角函数展开形式的频谱
第三部分 信号的处理和分析 广东工业大学机电工程学院 频谱图的概念 工程上习惯将计算结果用图形方式表示,以 fn ( ω n ) 为 横坐标, b n 、 a n为纵坐标画图,称为幅值谱图;以 fn为横 坐标, A n、 为纵坐标画图,则称为幅值-相位谱;以 fn 为横坐标, 为纵坐标画图,则称为功率谱。 n 2 A n 图例 指数展开形式的频谱三角函数展开形式的频谱

第三部分信号的处理和分析广东工业大学机电工程学院 例:方波信号的频谱展开 4A x()= s1n26花 8不驰1 (-A(-T12<t0 (0<t<T12) 式肿,n=123,西4=万 图示: An 035a 0 傅里叶变换的 0 演示 -z/2
第三部分 信号的处理和分析 广东工业大学机电工程学院 例:方波信号的频谱展开 图示: 0 0 2 n 1,2,3, , ; T 式中, 傅里叶变换的 演示

第三部分信号的处理和分析广东工业大学机电工程学院 周期信号的频谱特点 (1)离散性:是离散谱,每一条谱 线表示一个谐波分量;谱线的高 度代表幅值和相位的大小。 (2)谐波性:谱线只出现在基波及 00350 各次谐波的频率处。 (3)收敛性:满足狄里赫利条件的 周期信号,其谐波幅值随谐波 频率的增大而减小。 因此,工程测量中没有必要取 次数过高的谐波分量。 信号的带宽:按谐波幅值下降的程度来定义
第三部分 信号的处理和分析 广东工业大学机电工程学院 周期信号的频谱特点 (1)离散性:是离散谱,每一条谱 线表示一个谐波分量; 谱线的高 度代表幅值和相位的大小。 (2)谐波性:谱线只出现在基波及 各次谐波的频率处。 (3)收敛性:满足狄里赫利条件的 周期信号,其谐波幅值随谐波 频率的增大而减小 。 因此,工程测量中没有必要取 次数过高的谐波分量。 信号的带宽:按谐波幅值下降的程度来定义
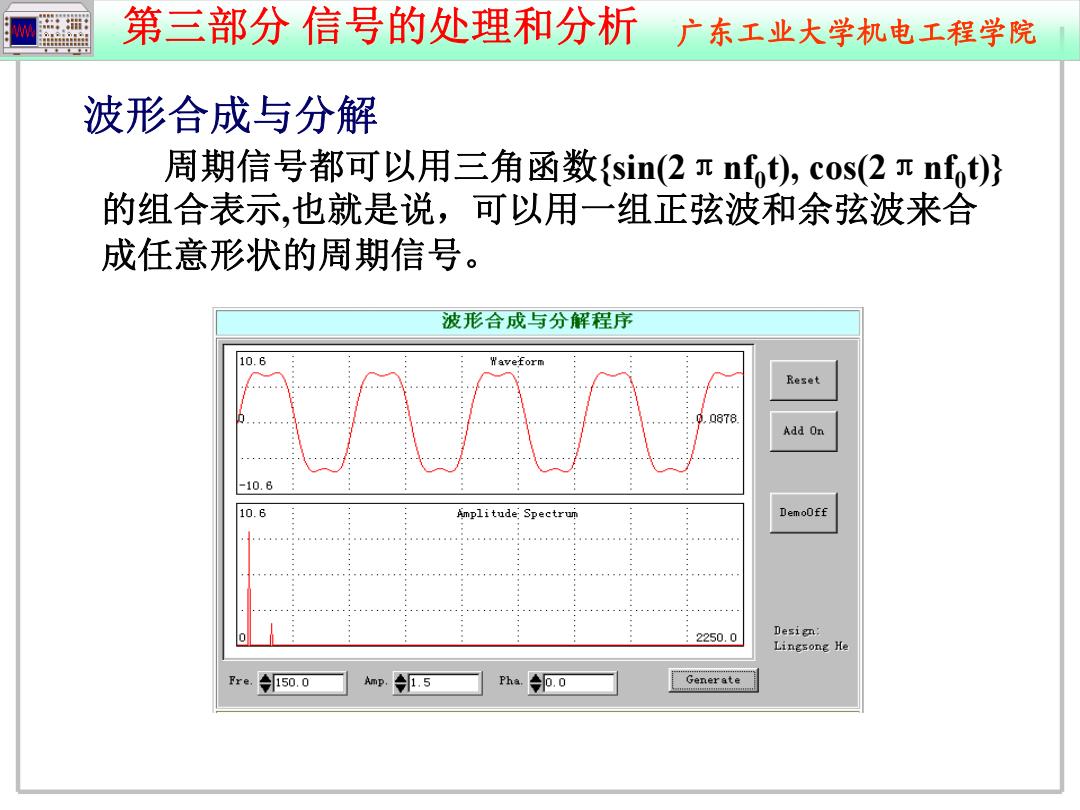
第三部分信号的处理和分析广东工业大学机电工程学院 波形合成与分解 周期信号都可以用三角函数{sin(2rnf),cos(2兀nf)} 的组合表示,也就是说,可以用一组正弦波和余弦波来合 成任意形状的周期信号。 波形合成与分解程序 10.6 Waveform 4 Reset 44年 44年4444 44 44 Q878 Add On -10.6 10.6 Spectru DemoOff 2250.0 Desig: Lingsong He Fre. 50.0 Amp. 1.5 Pha. p.0 Generate
第三部分 信号的处理和分析 广东工业大学机电工程学院 波形合成与分解 周期信号都可以用三角函数{sin(2 πnf0 t), cos(2 πnf0 t)} 的组合表示,也就是说,可以用一组正弦波和余弦波来合 成任意形状的周期信号

第三部分信号的处理和分析广东工业大学机电工程学院 3.非周期信号的频谱分析 非周期信号是时间上不会重复出现的信号,一般为时 域有限信号,具有收敛可积条件,其能量为有限值。这种 信号的频域分析手段是傅立叶变换(指数展开)。 x(t)=X(f)enmdf X (f)=X (f)e() X(f)=Re[X(f)]+Im[X()] X(f)=x(0e2d→ )=arctg 或 x(t)=X(o)eldo X(o)=x()e“adh
第三部分 信号的处理和分析 广东工业大学机电工程学院 3. 非周期信号的频谱分析 非周期信号是时间上不会重复出现的信号,一般为时 域有限信号,具有收敛可积条件,其能量为有限值。这种 信号的频域分析手段是傅立叶变换(指数展开)。 xt X e d X x t e dt j t j t () ( ) ( ) () 1 2 或 x t X f e df X f x t e dt j ft j ft () ( ) ( ) () 2 2 )( )()( fj efXfX )]([Im)]([Re)( 2 2 fXfXfX )](Re[ )](Im[ )( fX fX arctgf