
第三部分信号的处理和分析 广东工业大学机电工程学院 与周期信号相似,非周期信号也可以分解为许多不同 频率分量的谐波和,所不同的是,由于非周期信号的周期 T→∞,基频f=2T→df,它包含了从零到无穷大的所有 频率分量,谱线开始连续。各频率分量的幅值为X(①df, 表示幅值密度函数。 另外,与周期信号不同的是,非周期信号的谱线出现 在0,fmax的各连续频率值上,这种频谱称为连续谱。 指数展 三角函数数展 三角函数展开 信虚频谱仙) 开信号幅值谱(A)》 信号功率谱(A2) 0. 0.1 0.01 -0.1 0 1250 1250 信号实频谱(a) 信号相位谱(中》 0.1 180 人人人人人人N -180 (Hz) 1250 (Hz) 1250 (Hz) 1250
第三部分 信号的处理和分析 广东工业大学机电工程学院 与周期信号相似,非周期信号也可以分解为许多不同 频率分量的谐波和,所不同的是,由于非周期信号的周期 T ∞,基频 f 0 =2 π/T df,它包含了从零到无穷大的所有 频率分量,谱线开始连续。各频率分量的幅值为X(f)df , 表示幅值密度函数。 另外,与周期信号不同的是,非周期信号的谱线出现 在0,f max的各连续频率值上,这种频谱称为连续谱。 指数展 开 三角函数数展 开 三角函数展开

第三部分信号的处理和分析广东工业大学机电工程学院 4.傅立叶变换的性质 线性 ax(t)+by(t) ax(@)+bY(o 利用傅立叶变换的性质 对称性 X(0 2πr(-D) 可以由已知变换直接求得 一 些末知变换。 尺度变换 x(kt) 已知信号x()的傅氏变换为 时移特性 x(t±t) I(w)etia, F[x(t)]=X(@) 频移特性 x()eFjoo! X(o±) d*x(t) 那么利用尺度变换性质求得 微分特性 dr (jo)X(o) x(kt)的傅氏变换为 x爱 积分特性 X(c) J⊙
第三部分 信号的处理和分析 广东工业大学机电工程学院 4. 傅立叶变换的性质 利用傅立叶变换的性质 可以由已知变换直接求得 一些末知变换 。 已知信号x(t)的傅氏变换为 1 [ ( )] X ( ) k k F x kt 那么利用尺度变换性质求得 x (kt)的傅氏变换为 Fxt [ ( )] X ( )

第三部分信号的处理和分析广东工业大学机电工程学院 5.频谱分析的应用 频谱分析主要用于识别信号中的周期分量,是信号分析 中最常用的一种手段。 案例:在齿轮箱故障诊断 通过齿轮箱振动信号频谱分 析,确定最大频率分量,然后 根据机床转速和传动链,找出 故障齿轮
第三部分 信号的处理和分析 广东工业大学机电工程学院 5. 频谱分析的应用 频谱分析主要用于识别信号中的周期分量,是信号分析 中最常用的一种手段。 案例:在齿轮箱故障诊断 通过齿轮箱振动信号频谱分 析,确定最大频率分量,然后 根据机床转速和传动链,找出 故障齿轮
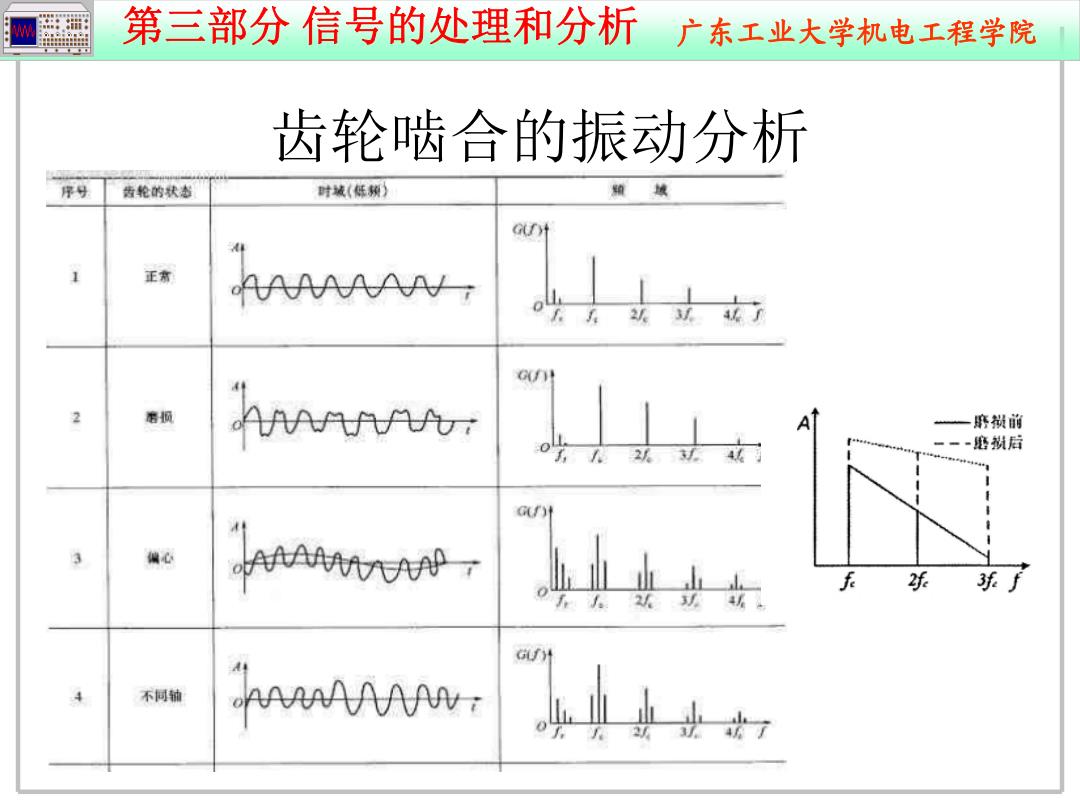
w 第三部分信号的处理和分析广东工业大学机电工程学院 齿轮啮合的振动分析 序号 告轮的状态 时城(低频) 箱 GUyt 正常 AAAAAAN G 香损 AAAAAAA 一靡制前 02或 4 一一一磨捌后 G) 偏心 AAAAMTAA7 2乐 3乐f f23 不同轴 AAAAAAAAN
第三部分 信号的处理和分析 广东工业大学机电工程学院 齿轮啮合的振动分析
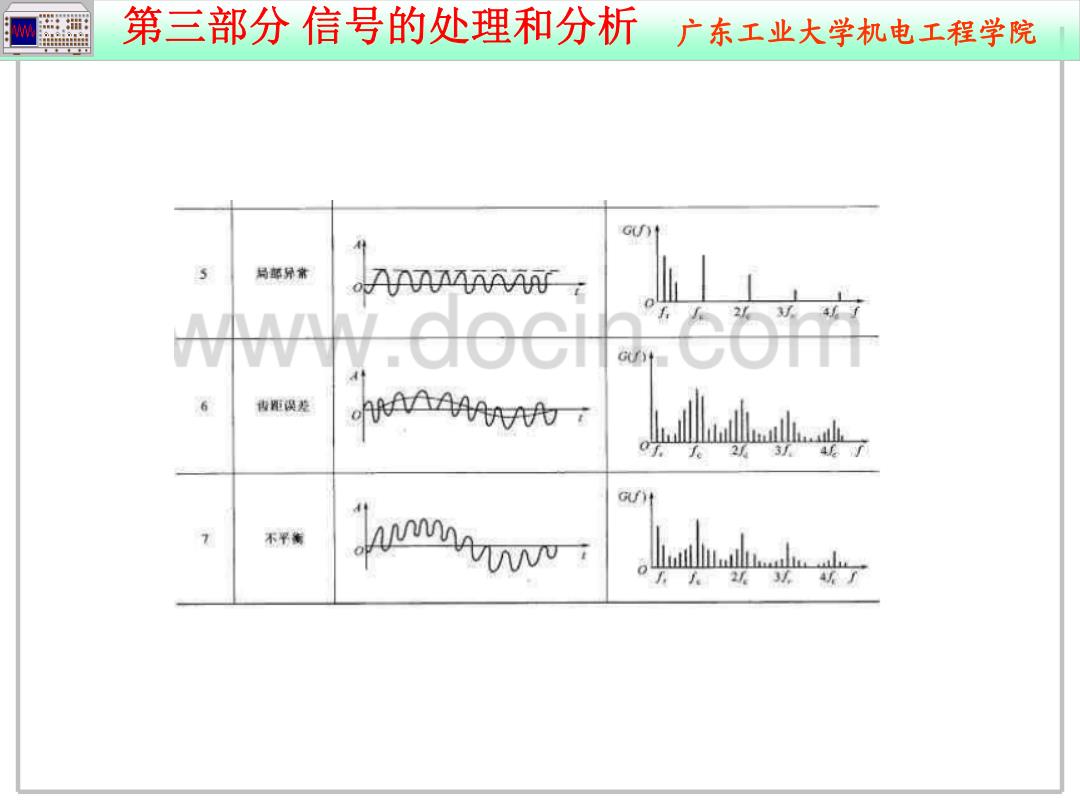
w 洲 第三部分信号的处理和分析广东工业大学机电工程学院 cU) 马邮异常 AAAMAM 传距误差 MAAAAA 不平衡
第三部分 信号的处理和分析 广东工业大学机电工程学院