第三部分信号的处理和分析广东工业大学机电工程学院 如图所示周期方波的时域表达式为 x国 x(t)=x(t+nTo) A 0<t< T A x()= 2 2 -A <<0 2 -A 00 x(t)= 元 3ma-小-enau兮na+nw+) 式中,n=l234 2n
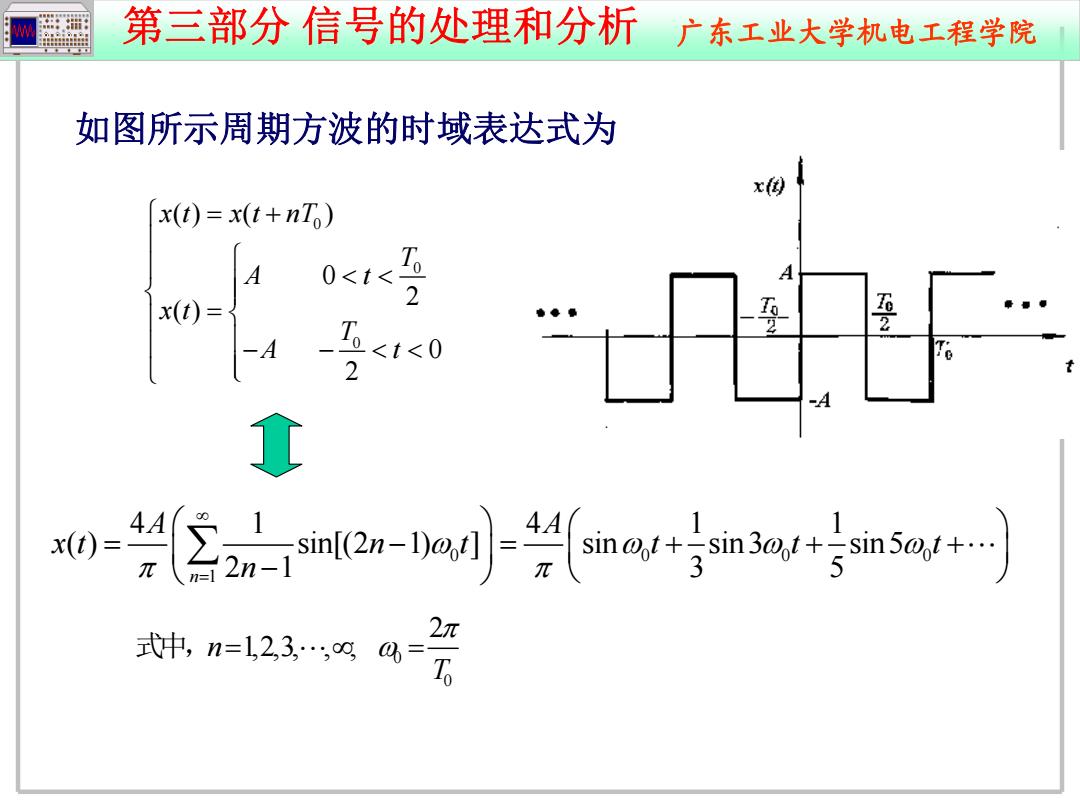
第三部分 信号的处理和分析 广东工业大学机电工程学院 如图所示周期方波的时域表达式为 0 0 0 () ( ) 0 2 ( ) 0 2 x t x t nT T A t x t T A t 0 000 1 41 4 1 1 ( ) sin[(2 1) ] sin sin3 sin5 n 21 3 5 A A xt n t t t t n 0 0 2 n 1,2,3, , ; T 式中,

第三部分信号的处理和分析广东工业大学机电工程学院 时域分析只能反映信号的幅值随时间的变化情况,除 单频率分量的简谐波外,很难明确揭示信号的频率组成和 各频率分量大小。 图例:受噪声干扰的多频率成分信号 言号波形 L 5 t/s 信号功率谱 25 £/Hz 1250
第三部分 信号的处理和分析 广东工业大学机电工程学院 时域分析只能反映信号的幅值随时间的变化情况,除 单频率分量的简谐波外,很难明确揭示信号的频率组成和 各频率分量大小。 图例:受噪声干扰的多频率成分信号
第三部分信号的处理和分析 广东工业大学机电工程学院 时域分析与频域分析的关系 信号的频谱X(①代表 了信号在不同频率分 量处信号成分的大 幅值 小,它能够提供比时 域信号波形更直观, 丰富的信息。 时间 时域分析 频域分析
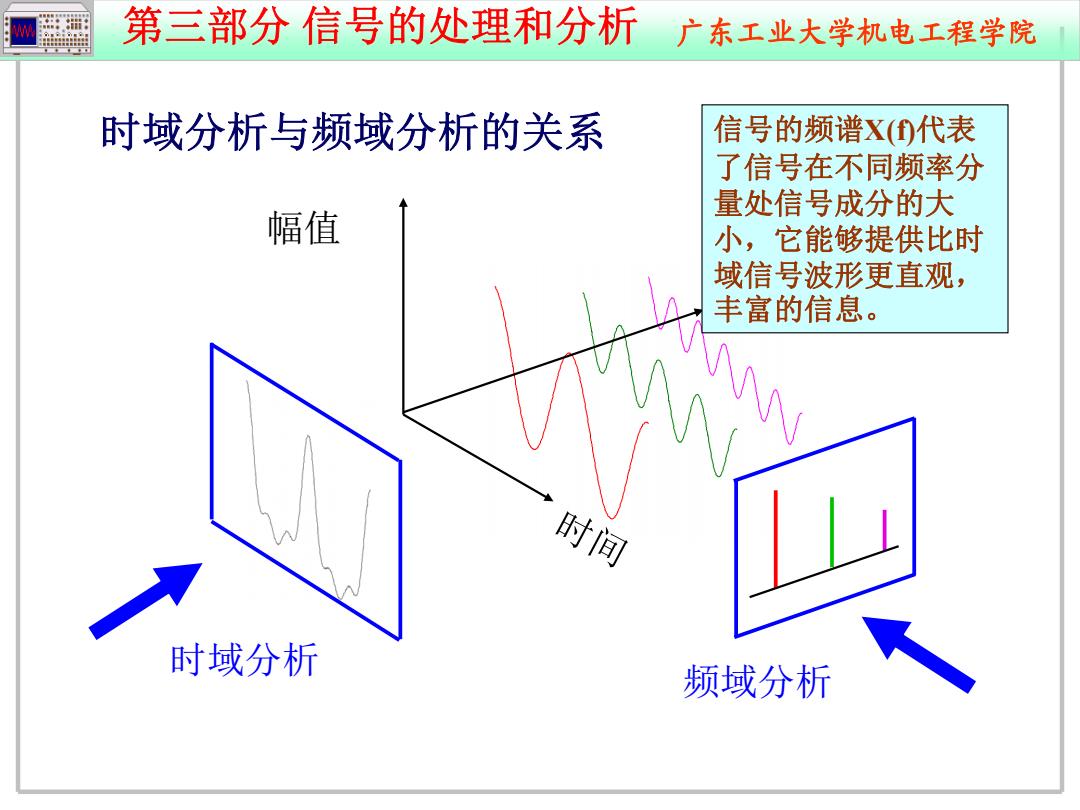
第三部分 信号的处理和分析 广东工业大学机电工程学院 时间 幅值 频率 时域分析 频域分析 信号的频谱X(f)代表 了信号在不同频率分 量处信号成分的大 小,它能够提供比时 域信号波形更直观, 丰富的信息。 时域分析与频域分析的关系

第三部分信号的处理和分析广东工业大学机电工程学院 2.周期信号的频谱分析 周期信号是经过一定时间可以重复出现的信号,满足条件 x(t)=x(t+nT) 任何周期函数,都可以展开成正交函数线性组合的无穷 级数,如三角函数集cosn@,t,sinnoot} 的傅里叶级数。 傅里叶级数的表达形式: x0)=受+∑(a,cosno,t+h,sinn@,f)) n=] (n=1,2,3,…) x0=号+∑A,cosf1@,1-p,n=l2 n 傅里叶展开的 余弦表示方式
第三部分 信号的处理和分析 广东工业大学机电工程学院 2. 周期信号的频谱分析 周期信号是经过一定时间可以重复出现的信号,满足条件 x ( t )= x ( t + nT ) 任何周期函数,都可以展开成正交函数线性组合的无穷 级数,如三角函数集 0 0tntn }sin,{cos 的傅里叶级数。 傅里叶级数的表达形式: 1 2 0 0 1 2 0 )( cos( ,...)2,1(), cos()( )sin 0 0 n n n a n n n a ntnAtx tnbtnatx n ,...)3,,2,1( 傅里叶展开的 余弦表示方式

第三部分信号的处理和分析广东工业大学机电工程学院 2.周期信号的频谱分析 式中: x(t)dt; T一一周期, a.- T=2T/00: x(t)cos n@otdt; ①。一一基波圆频率 T/2 f=w0/2元 b=子2 x(t)sin nooldi; An van2+b2; arctg
第三部分 信号的处理和分析 广东工业大学机电工程学院 式中: ; ; ;sin)( ;cos)( ;)( 22 2/ 2/ 0 2 2/ 2/ 0 2 2/ 2/ 2 0 n n a b n n nn T T n T T T n T T T T arctg baA b tdtntx a tdtntx a dttx T――周期, T=2 π / ω 0; ω 0――基波圆频率 f0 = ω 0 /2 π 2. 周期信号的频谱分析