
例9.4,本例要考虑实指数和复指数之和的信号为 x(t》=e2(t)+et(w3t)u(t) (9.24) 利用胶拉关系,可写为 x(e)=[e2+ea-+e+0](e) 那么x(x)的拉普拉斯变换就能表示成 X(s)["eu(t)e-"de +2e--0e“d )edt (9.25) (9.25)式中的每一个积分都代表了在例9.1中所调到过的拉普拉斯变换,即 eue2%>-2 (9.26 e-wx()-71 s+(1-3,2>-1 (9.27) e(u(1)1 5+(1+3)·%>-1 (9.28) 为了使这三个拉普拉斯变换都同时收敛,必须有见s}>-1,因此,x(t)的拉普拉斯变换为

,2+2(+-)+(d+3罚,%>-1 (9.29) 或者,合并为公共分母得 ead+ea(8ae2是2刀号 2s2+5s+12 si>-1 (9.30)
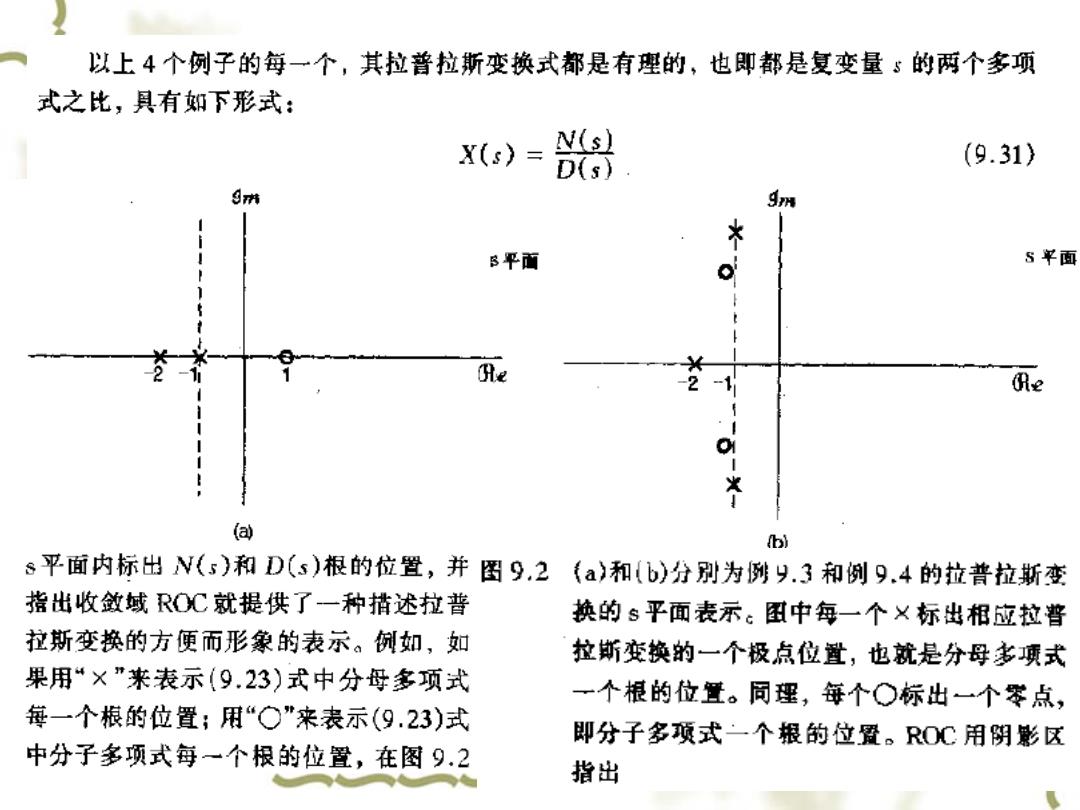
以上4个例子的每一个,其拉普拉斯变换式都是有理的,也即都是复变量5的两个多项 式之比,具有如下形式: X(s)= N(s) D(s) (9.31) 9州 B平面 S¥面 Re 价e * ( b s平面内标出N(s)和D(s)根的位置,并图9,2 {a)和(b)分别为例9.3和例9.4的拉普拉斯变 指出收敛域ROC就提供了一种措述拉普 换的s平面表示。图中每一个×标出相应拉普 拉斯变换的方便而形象的表示。例如,如 拉斯变换的一个极点位置,也就是分母多项式 果用“×”来表示(9.23)式中分母多项式 一个根的位置。同理,每个○标出一个零点, 每一个根的位置;用“○”来表示(9.23)式 即分子多项式一个报的位置。ROC用阴影区 中分子多项式每一个根的位置,在图9.2 指出

例9.5设信号x(t)为 x()=)-青eu(e)+子u() (9.32) (9.32)式中右边第二和第三项的拉普拉斯变换都可由例9.1求出,而单位冲激函数的拉普拉斯变 换可直接求出为 i(1=1mac)e4=1 (9.33) 该结果对任何s值都成立。这就是说,(t)}的ROC是整个s平面。利用这个结果。再与(9.32) 式其余两项一起就得出 x)=1-专中1+寸,2 s>2 (9.34) 或者 (s-1)3 X)=g+g-2》%>2 (9.35
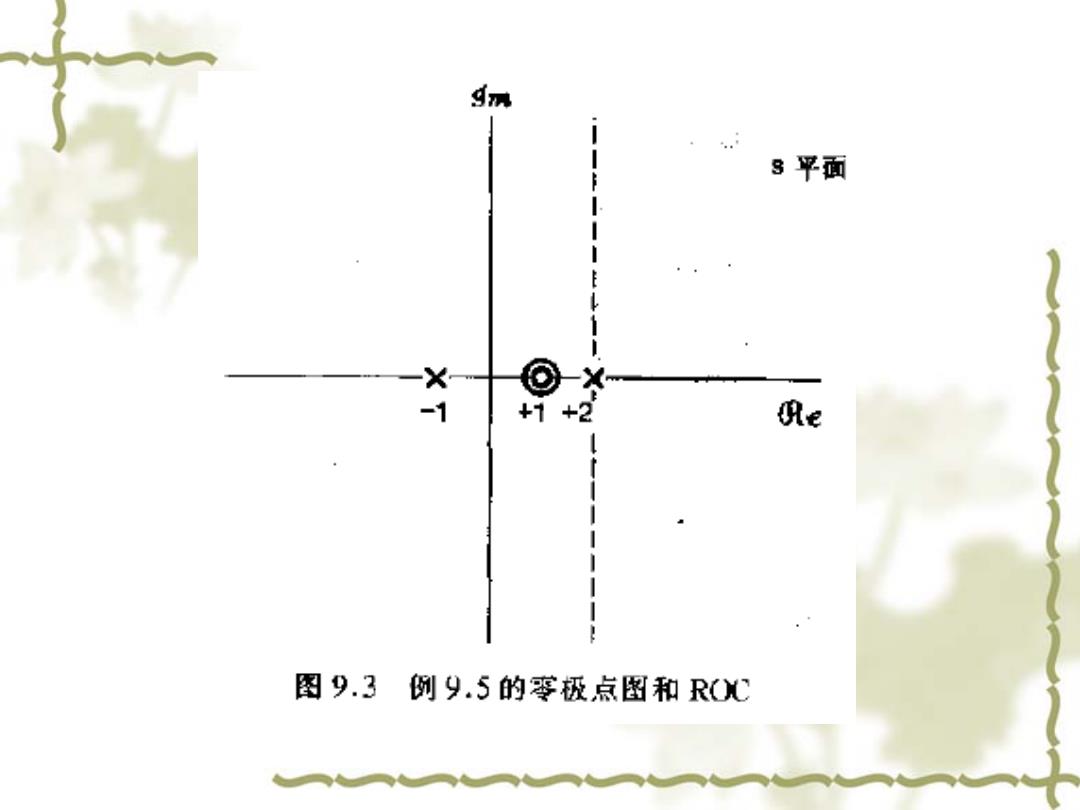
9m 3平面 E -1 +1 +2 吼e 图9.3例9.5的娶极点图和R(0C