
9.2拉普拉斯变换收敛域 从前面的讨论已经看到,拉普拉斯变换的全邵特性不仅要求X(s)的代数表示式,而且 还应该伴随着收敛域的说明。这一点在例9.1和例9.2中体现得最为明显:两个很不相同的 信号能够有完全相同的X(s)代数表示式,因此它们的拉普拉斯变换只有靠收敛域才能区分。 这一节将说明对各种信号在ROC上的某些具体限制。将会看到,理解了这些限制往往使我 们仅仅从X(s)的代数表示式和x()在时域中某些一般持征就能明确地给出或构成收敛域 ROC

性质1:X(s)的RCO℃在s平面内由平行于j轴的带状区域所组成。 这一性质来自于这样一个事实:X(s)的ROC是由这样一些s=。+j仙所组成,在那里 x(t)er的傅里叶变换收敛,也就是说,x(t)的拉普拉斯变换的ROC是由这样一些s值组 成的,对于这些;值,x(t)e是绝对可积的①,即 ∫lx)1ed<o (9.36) 因为这个条件只与,即s的实部有关,所以就得到性质1

性质2:对有理拉普拉斯变换来说,ROC内不包括任何极点。 这个性质,在到目前为止所研究的例子中都能很容易地看出。因为,在一个极点处, X(s)为无限大,(9.3)式的积分显然在极点处不收敛,所以ROC内不能包括屑于极点 的5值

性质3:如果x(t)是有限持续期,并且是绝对可积的,那么ROC就是整个 s平面。 这个结果背后的直观性由图9.4和图9.5可以想到。这就是,一个有限持续期的信号具 有这个性质,它在某一有限区间之外都是零,如图9.4所示。在图9.5()中画出了图9,4这 样的x(t)乘以一个衰减的指数函数,而在图9.5(b)则画出同一类型的信号乘以一个增长的
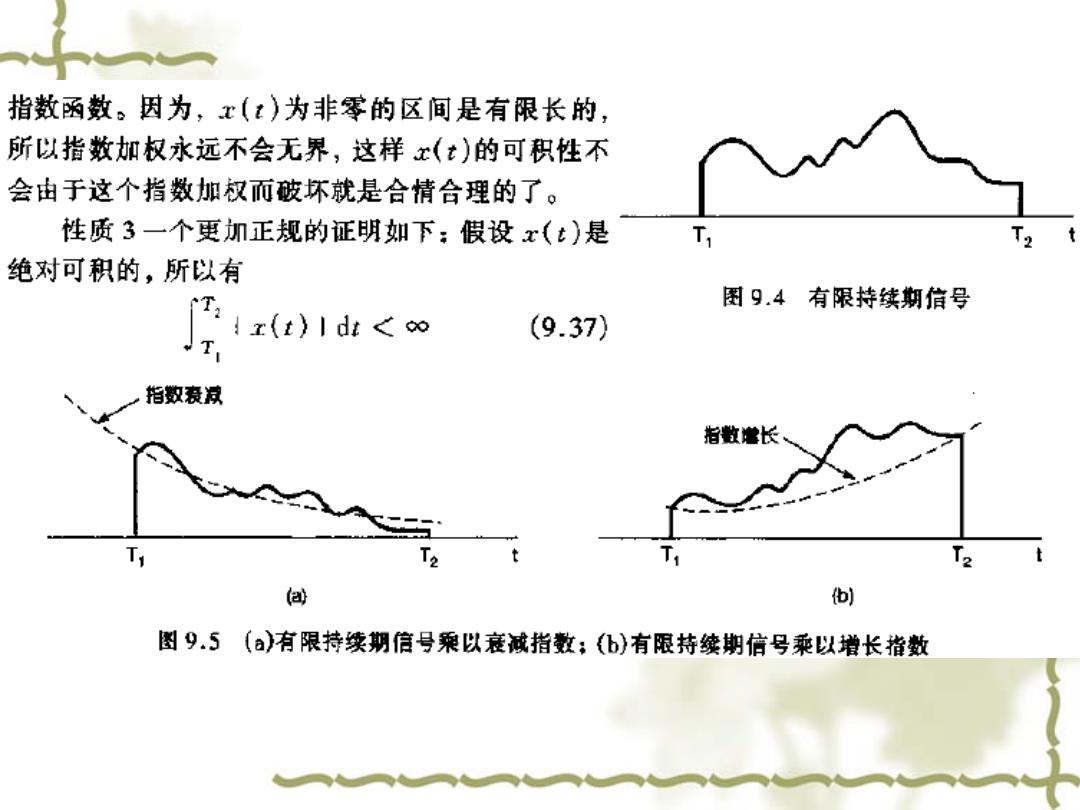
指数函数。因为,x()为非零的区间是有限长的, 所以指数加权永远不会无界,这样x(t)的可积性不 会由于这个指数加权而破坏就是合情合理的了。 性质3一个更加正规的证明如下:假设x(t)是 T 人 绝对可积的,所以有 T:z(t)1<∞ 图9.4有限持续期信号 (9.37) 指数衰汉 指数长 @ (b) 图9.5(a)有限持续期信号乘以衰诚指数:(b)有限持续期信号乘以增长指数