例4: 已知:Us2=4V,Us3=6V; K→1时, (mA =40mA K→2时, mA -60mA 求:K→3时, EKUs1+K2Ux K=1时,Ux=0 40=K]UsI K=2时,Ux=4V -60=KUs1+4K2 K=3时,Ux=-6V I=KUS1-6K2 解有:=190mA
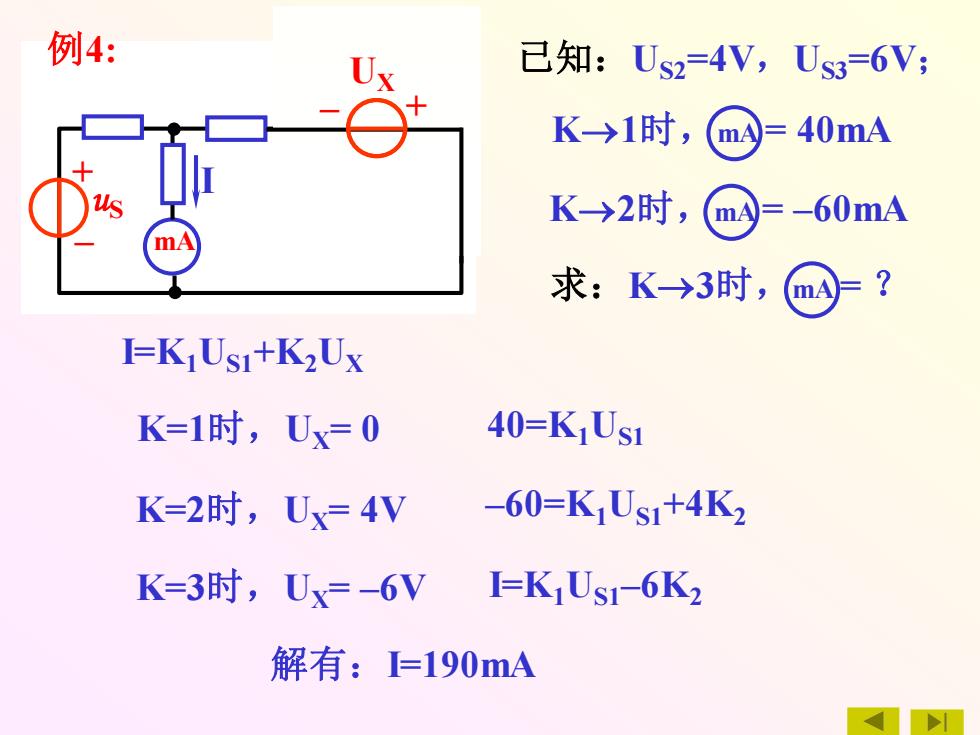
已知:US2=4V,US3=6V; 求:K→3时,mA = ? K→1时,mA = 40mA K→2时,mA = –60mA I=K1US1+K2UX K=1时,UX= 0 K=2时,UX= 4V K=3时,UX= –6V + – – + + – mA 1 2 3 S US1 US2 US3 + – – + + – mA 1 2 3 S uS I – + UX 例4: 40=K1US1 –60=K1US1+4K2 I=K1US1–6K2 解有:I=190mA

齐性定理 u=K14s1+K2ls2+K34s3+. 当只有一个独立电源时:u=Ks1 即:激励与响应成正比 45A423A42 ☐r=1A ∥2v 梯形电路 求:=? 解:设=1A则:Us=36V .I=KUs 号
齐性定理 u=K1uS1+K2uS2+K3uS3+ . 当只有一个独立电源时: u=K1uS1 即:激励与响应成正比 + – 8V 4Ω 12Ω 4Ω 4Ω 3Ω 2Ω I 梯形电路 求:I=? 解:设 I=1A 36V 1.5A 4.5A 6V 2V 2A 3A 12V 18V 则:US =36V ∵ I=KUS ∴I= US= = A I US 2 9 8 36 I=1A

$4一2替代定 理 R R2 R2 3A 10V 62 该支路可以是含源的, 也可以是无源的。但一 般不应当含有受控源或 该支路的电压、电流为 其它支路中受控源的控 制量
§ 4 — 2 替代定 理 + – + – uS1 R1 iS uS2 R2 R3 该支路可以是含源的, 也可以是无源的。但一 般不应当含有受控源或 该支路的电压、电流为 其它支路中受控源的控 制量。 10V 3A + – + – uS1 R1 iS R2 10V + – uS1 R1 iS R2 3A