
心号与事安 §1,3信号的运算 •信号的自变量的变换 平移反褶 尺度 一般情况 ·微分和积分 ·两信号相加或相乘 *米 新疆大学信息科学与工程学院电子系 2011.1 退出 开始
新疆大学信息科学与工程学院电子系 2011.1 §1.3 信号的运算 •信号的自变量的变换 平移 反褶 尺度 一般情况 •微分和积分 •两信号相加或相乘

信号的自变量的变换 (波形变换 1.信号的移位 2.信号的反褶 3.信号的展缩(尺度变换) 4.一般情况
X 第 2 一.信号的自变量的变换(波形变换)页 1.信号的移位 2.信号的反褶 3.信号的展缩(尺度变换) 4.一般情况

1.信号的平移 f()→f(t-) 将信号fd)沿t轴平移x即得时移信号ft-),x为常数 x>0,右移(滞后) x<0,左移(超前 例: f(t +1)的波形? f头) 宗量相同,函数值相同,求新坐标 {Um{en{ea, )了t=-1
X 第 3 页 O t − 1 1 1 f (t) 1.信号的平移 f (t + 1) 将信号f (t)沿t 轴平移 即得时移信号f (t − ), 为常数 f (t) → f (t − ) 例: + = = − + = + = = = ( 1) 1 1 ( 1) 1 1 0 ( ) 1 0 f t t f t t f t t > 0,右移(滞后) < 0,左移(超前) 宗量相同,函数值相同,求新坐标 O t f (t) − 1 1 1 f(t+1)的波形?
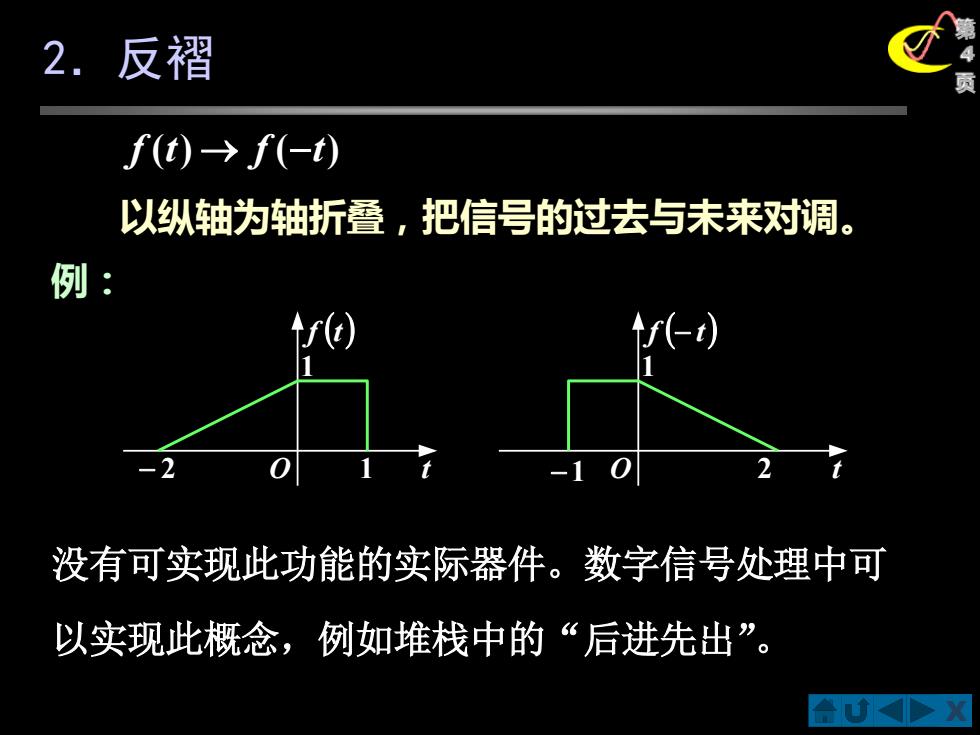
2. 反褶 f(t)→f(-) 以纵轴为轴折叠,把信号的过去与未来对调。 例 没有可实现此功能的实际器件。数字信号处理中可 以实现此概念,例如堆栈中的“后进先出”。 合UD
X 第 4 页 没有可实现此功能的实际器件。数字信号处理中可 以实现此概念,例如堆栈中的“后进先出”。 2.反褶 f (t) → f (−t) 例: 以纵轴为轴折叠,把信号的过去与未来对调。 − 2 O 1 1 f (t) t −1 O 2 1 f (− t) t
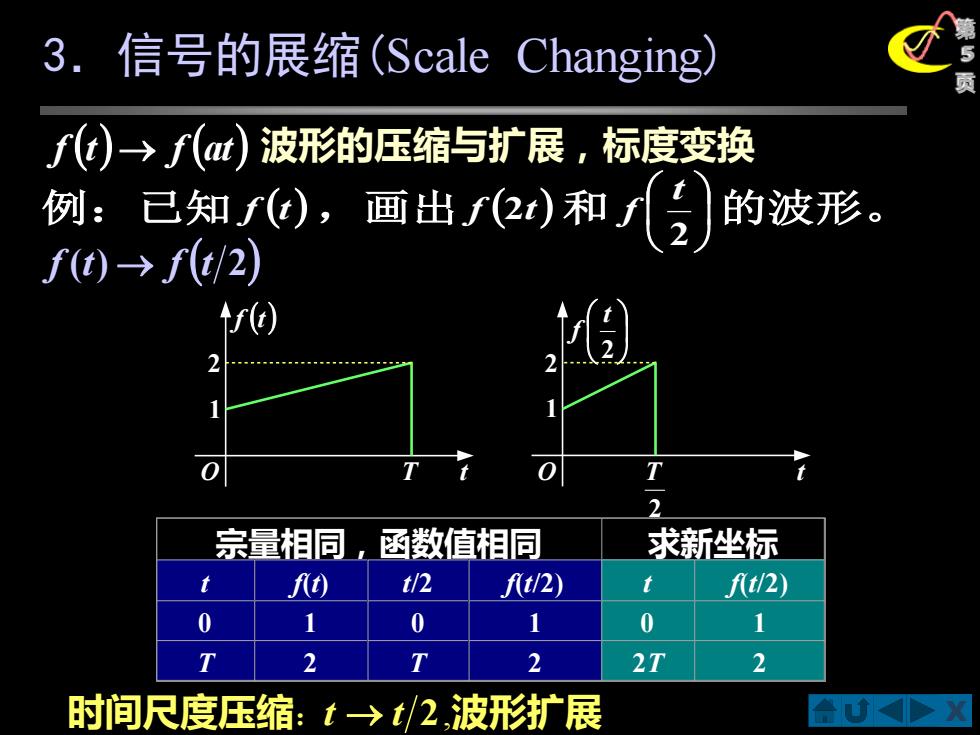
3.信号的展缩(Scale Changing) fd)→f(d)波形的压缩与扩展,标度变换 例:已知0,画出/和 的波形 ft)→ft/2) f 宗量相同,函数值相同 求新坐标 ) t/2 ft/2) t ft/2) 0 1 0 1 0 1 T 2 T 2 2T 2 时间尺度压缩:t→t/2,波形扩展
X 第 5 页 3.信号的展缩(Scale Changing) 例:已知 f (t) ,画出 f (2t) 和 2 t f 的波形。 波形的压缩与扩展,标度变换 宗量相同,函数值相同 求新坐标 t f(t) t/2 f(t/2) t f(t/2) 0 1 0 1 0 1 T 2 T 2 2T 2 f (t) → f (t 2) 时间尺度压缩: t → t 2 ,波形扩展 f (t) → f (at) O T 2 1 f (t) t O 2 T 2 1 2 t f t