
5.2 Systems Characterized by Linear Constant-Coefficient Difference Equation Linear Constant-coefficient Difference equation 之a[-]-之A-k] For LTΠSystems Z-transform 空ae)之AXe 之z 区-2rgm: 29
5.2 Systems Characterized by Linear Constant-Coefficient Difference Equation ◆Linear Constant-coefficient Difference equation 0 0 N M k k k k a y n k b x n k = = − = − ( ) ( ) 0 0 N M k k k k k k a z Y z b z X z − − = = = ( ) ( ) ( ) 0 0 N M k k k k k k a z Y z b z X z − − = = = ( ) 0 0 M k k k N k k k b z H z a z − = − = = 29 For LTI Systems Z-transform

5.2 Systems Characterized by Linear Constant-coefficient Difference equation ◆For an LTI system: M Y() ∑bz (1-c2) H(X k=0 bo k=1 Π(1-dz) k=0 k=1 ◆its poles and zeros: 1-Cz1=0 → Z=Ck:zero 1-dz1=0 → z=d:pole 30
1 1 0 : k k c z z c zero − − = = ( ) ( ) ( ) ( ) ( ) 1 1 1 0 0 0 0 1 1 1 M k k k N k M k N k k k k k b z Y z b H z X z a z z c a d z − = − − − = = = = = = − − 1 1 0 : k k d z z d pole − − = = ◆For an LTI system: ◆its poles and zeros: 5.2 Systems Characterized by Linear Constant-coefficient Difference equation 30

Ex.5.1 find difference equation for second-order System function Solution: (1+21)2 1+2z1+z2 Y(a -1 3 1+ -2 X(2) 4 8 1+ 4 8e)-2z+ke 网+4n-小-n-2]=+2xn-+n-2] 31
Ex. 5.1 find difference equation for second-order System function ( ) ( ) 2 1 1 1 1 1 3 1 1 2 4 z H z z z − − − + = − + z z Y(z) ( z z )X (z) 1 2 1 2 1 2 8 3 4 1 1 − − − − = + + + − 2 2 1 2 8 3 1 4 1 y n + y n − − y n − = x n + x n − + x n − ( ) ( ) 1 2 1 2 1 2 1 3 1 4 8 z z Y z X z z z − − − − + + = = + − Solution: 31

5.2.1 Stability and Causality The difference equation of a LTI system does not uniquely specify the impulse response. mo可 三--之i利品H I >a k=0 Each ROC of the system function will lead to a different impulse response; but they will all correspond to the same difference equation. 第3章3.2节有介绍系统时域特性与H(Z)收敛域关系的内容,3.5再 联系差分方程也介绍了一下,这里强化以导出最小相位系统概念
5.2.1 Stability and Causality ◆The difference equation of a LTI system does not uniquely specify the impulse response. 32 ◆Each ROC of the system function will lead to a different impulse response; 0 0 N M k k k k a y n k b x n k = = − = − ( ) 0 0 M k k k N k k k b z H z a z − = − = = ◆but they will all correspond to the same difference equation. x n =n LTI ➢ 第3章3.2节有介绍系统时域特性与H(z)收敛域关系的内容, 3.5再 联系差分方程也介绍了一下, 这里强化以导出最小相位系统概念. Z
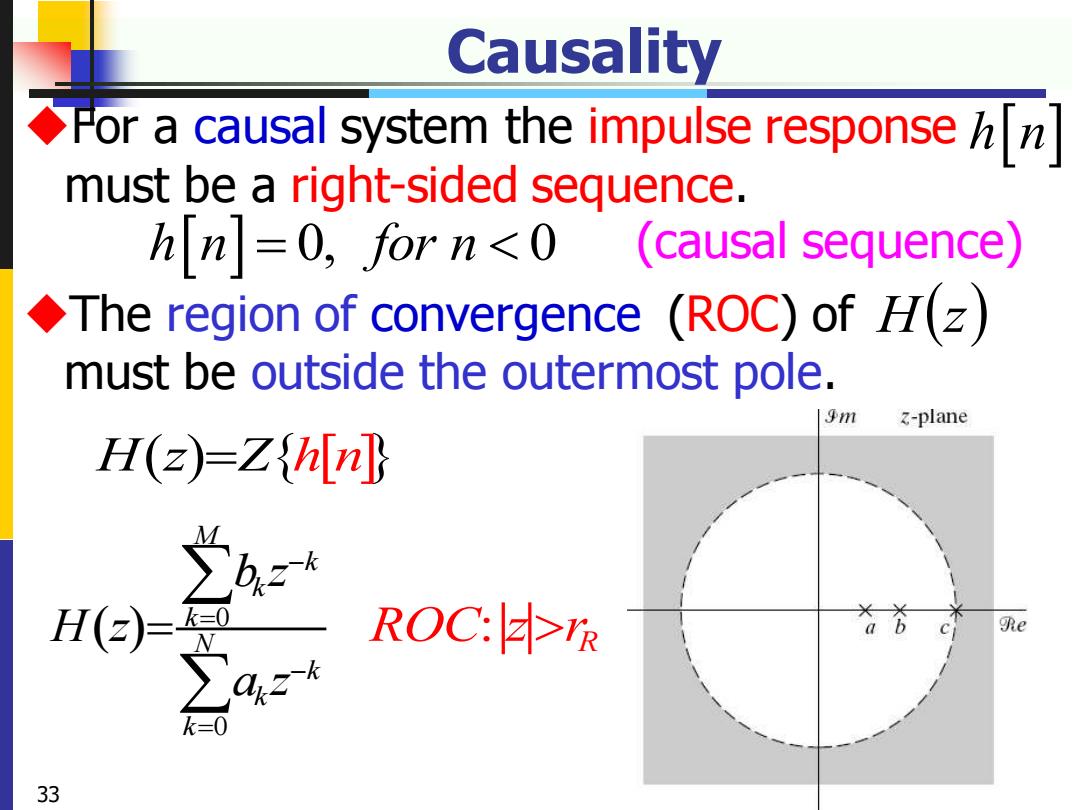
Causality Por a causal system the impulse response hn must be a right-sided sequence. hn =0,for n<0 (causal sequence) The region of convergence (ROC)of H(z) must be outside the outermost pole. gm 3-plane H(=Zhin H(2)=O ROC:>TR Re k=0 33
Causality ◆For a causal system the impulse response must be a right-sided sequence. h n ◆The region of convergence (ROC) of must be outside the outermost pole. H(z) h n for n = 0, 0 33 H z( )=Zhn : ( ) ROC z r R 0 0 M k k k N k k k b z H z a z − = − = = (causal sequence)