
Chapter 3 The z-Transform ◆3.0 Introduction ◆3.1z-Transform 3.2 Properties of the Region of Convergence for the z-transform 3.3 The inverse z-Transform 3.4 z-Transform Properties 3.5 z-Transform and LTI Systems 3.6 the Unilateral z-Transform 2
2 Chapter 3 The z-Transform ◆3.0 Introduction ◆3.1 z-Transform ◆3.2 Properties of the Region of Convergence for the z-transform ◆3.3 The inverse z-Transform ◆3.4 z-Transform Properties ◆3.5 z-Transform and LTI Systems ◆3.6 the Unilateral z-Transform

3.0 Introduction Fourier transform plays a key role in analyzing and representing discrete-time signals and systems,but does not converge for all signals. -品=24 1-ae jo 1-ae -ae Continuous systems:Laplace transform is a generalization of the Fourier transform. Discrete systems z-transform,which is a generalization of DTFT,converges for a broader class of signals 3
3 3.0 Introduction ◆Fourier transform plays a key role in analyzing and representing discrete-time signals and systems, but does not converge for all signals. ◆Continuous systems: Laplace transform is a generalization of the Fourier transform. ◆Discrete systems : z-transform, which is a generalization of DTFT, converges for a broader class of signals. xn a un n = a 1 DTFT 0 1 1 j ae − = − n n jwn a u n e =− − ! 1 ( ) 1 j j ae ae − − − = −

3.1 z-Transform X(e)=∑x[neom→∑n]z" n=-o0 Z=reia ◆If elo>z,Fourier transform→z-transform z-Transform:two-sided,bilateral z-transform X(z)=∑x[nzn=z{x[n]} n=-00 m←2→X(z) ◆one-sided, unilateral z-transform UX(z)=z)=∑x[nz n=0 Go 5
5 3.1 z-Transform ( ) j n j n X e x n e =− − = ( ) [ ] n n X z x n x n z =− − = = Z 0 n n x n z − = = ◆one-sided, unilateral z-transform ◆z-Transform: two-sided, bilateral z-transform x n X z [ ]⎯→ ( ) Z ◆If , j e z → Fourier transform z-transform n n x n z =− → − j Z = reGo UX z( ) =

Relationship between z-transform and Fourier transform Express the z in polar form as X(z)=∑x[n]z” =X(rem)=∑(x[nlr")emm n=-o0 z-transform is the Fourier transform of the product of xn and( (the exponential sequence ) Ifr=Z-l,X(Z)→X(eo) 6
6 ◆Express the z in polar form as Relationship between z-transform and Fourier transform j Z = re ( ) ( ) j n j n n X e re x n r − = − − = = ◆z-transform is the Fourier transform of the product of and (the exponential sequence ). x n n r − If X Z r Z = = 1, ( ) ( ) n n X z x n z =− − = ( ) j X e
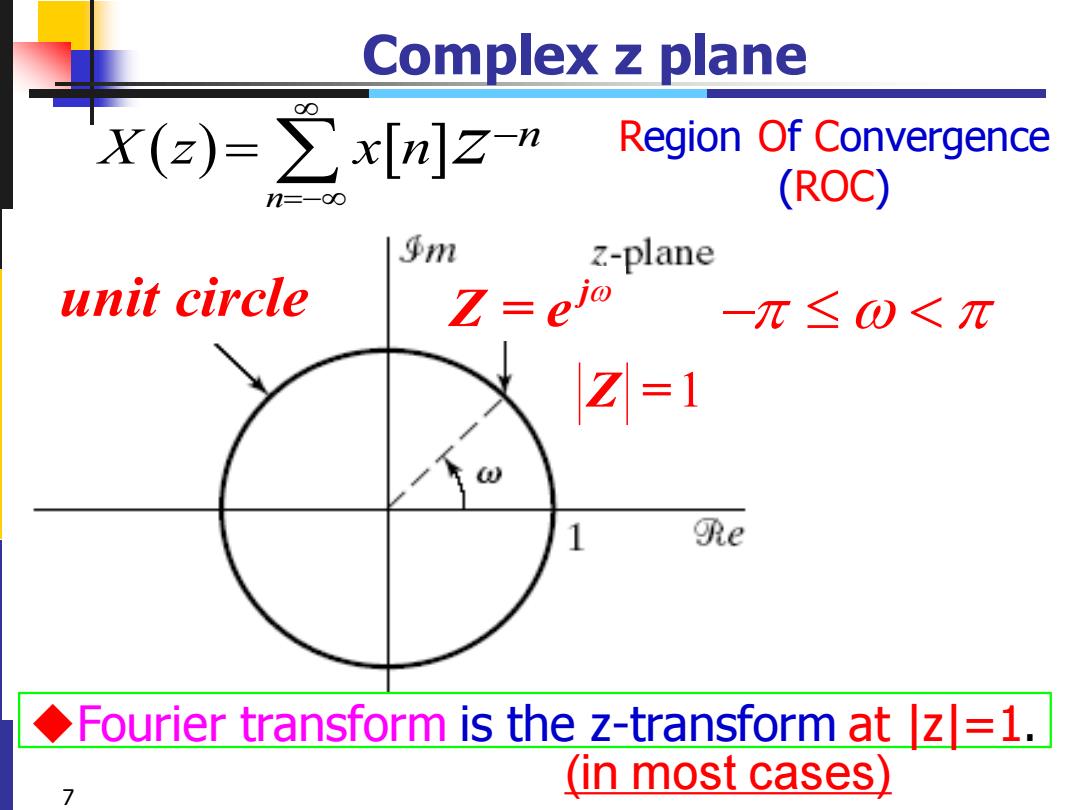
Complex z plane X(z)=∑x[n]z-n Region Of Convergence n=-00 (ROC) 乎m Z-plane unit circle Z=eio -π≤①<π Z=1 1 e Fourier transform is the z-transform at z|=1. (in most cases) 7
7 Complex z plane ( ) n n X z x n z =− − = j unit circle Z = e − Z =1 Region Of Convergence (ROC) ◆Fourier transform is the z-transform at |z|=1. (in most cases)