山东大学：《生物医学信号处理 Biomedical Signal Processing》精品课程教学资源（PPT课件讲稿）Chapter 07 Filter Design Techniques

Chapter 7 Filter Design Techniques ◆7.0 Introduction 7.1 Filter Specifications 7.2 Design of Discrete-Time IIR Filters From Continuous-Time Filters 7.3 Discrete-Time Butterworth,Chebyshev and Elliptic Filters 7.4 Frequency Transformations of Lowpass IIR Filters 7.5 Design of FIR Filters by Windowing 7.6 Examples of FIR Filters Design by the Kaiser Window Method 2

2 Chapter 7 Filter Design Techniques ◆7.0 Introduction ◆7.1 Filter Specifications ◆7.2 Design of Discrete-Time IIR Filters From Continuous-Time Filters ◆7.3 Discrete-Time Butterworth, Chebyshev and Elliptic Filters ◆7.4 Frequency Transformations of Lowpass IIR Filters ◆7.5 Design of FIR Filters by Windowing ◆7.6 Examples of FIR Filters Design by the Kaiser Window Method

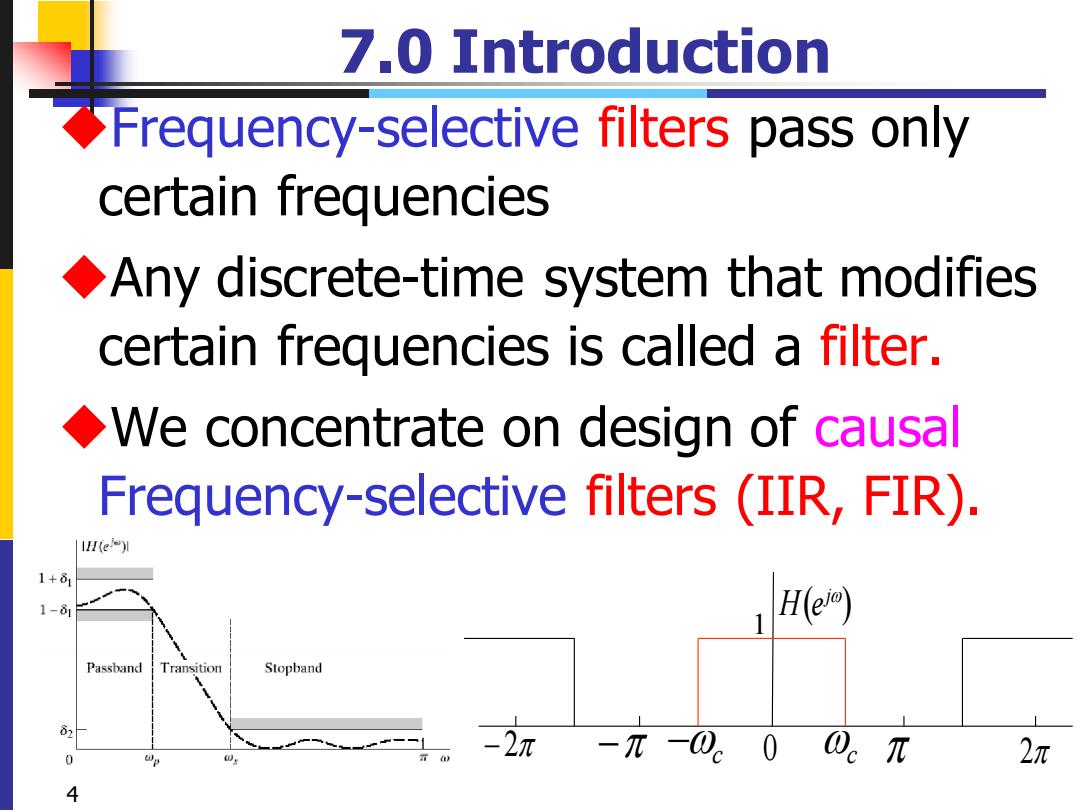
7.0 Introduction Frequency-selective filters pass only certain frequencies Any discrete-time system that modifies certain frequencies is called a filter. We concentrate on design of causal Frequency-selective filters (IIR,FIR). IH(e) 1+81 1-81 He） Passband Transition Stopband -2π-π-0.0 0 p 0e元 2n 4

4 7.0 Introduction ◆Frequency-selective filters pass only certain frequencies ◆Any discrete-time system that modifies certain frequencies is called a filter. ◆We concentrate on design of causal Frequency-selective filters (IIR, FIR). ( ) j H e  − 2 − −c 0 c  2 1

5.1.1 Ideal Frequency-Selective Filters idea owpas fiter: ◆Noncausal,not in computationally realizable ◆no phase distortion H( -2π-7π-00 2π 5

5.1.1 Ideal Frequency-Selective Filters ◆Ideal lowpass filter: 5 ◆Noncausal, not computationally realizable ◆no phase distortion   sin , c lp n h n n   = −    n ( )  , | | , 0, | | j 1 c lp c H e        =   ( ) j H e  − 2 − −c 0 c  2 1

5.1.1 Ideal Frequency-Selective Filters Ideal highpass filter l-eH(e-e3e ◆Noncausal,not hmln]=8fn] sinan -o0<n<o0 computationally 元n realizable ◆no phase distortion H(e) -2元 0 2元 6

5.1.1 Ideal Frequency-Selective Filters ◆Ideal highpass filter     sin , c h n n hp n n n    = − −  − 2 − −c 0 c  2 ( ) H ej 1 6 ◆Noncausal, not computationally realizable ◆no phase distortion ( ) ( )  0, | | 1 1, | | j c hp c j Hlp e H e         − = =  

5.1.1 Ideal Frequency-Selective Filters Ideal bandpass filter hae）h.e）.ey6: others hon-sinon s nan -oo<n<oo πn πn .Noncausal,not computationally realizable ◆no phase distortion 1H(e） -π-02 02π 7

5.1.1 Ideal Frequency-Selective Filters ◆Ideal bandpass filter 0 c1 c1 − −  ( ) j H e  1 −c2 c2 7 ◆Noncausal, not computationally realizable ◆no phase distortion   2 1 sin , sin c c bp n n h n n n n     = − −  ( ) 1 ( ) ( )  1 2 2 , | | 0, j 1 lp j p c c l bp H ej oth s H H e er e         − = =