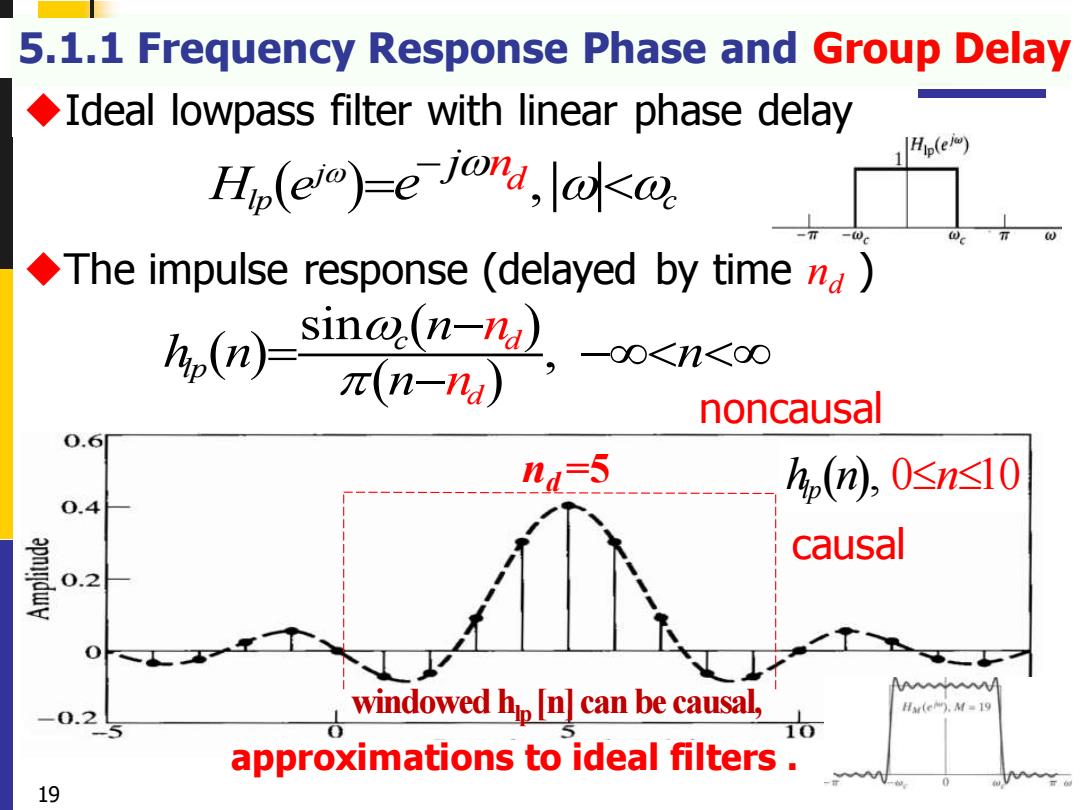
5.1.1 Frequency Response Phase and Group Delay Ideal lowpass filter with linear phase delay Hp(e) Hp(em)=e®h,ldko The impulse response(delayed by time n) ,(m)-s ina(n-na) -oo<n<oo π(n-na) noncausal 0.6 na=5 hp(n),O<ns10 0.4 causal 复 0.2 H(e).M=19 0.2 windowed hn can be causal, 10 approximations to ideal filters. 19
◆Ideal lowpass filter with linear phase delay ( ) ( ) ( ) sin , c d lp d n h n n n n n − = − − ◆The impulse response (delayed by time nd ) 5.1.1 Frequency Response Phase and Group Delay 19 nd =5 ( ) , j lp c d j n H e e − = noncausal causal approximations to ideal filters .h n lp( ), 0 1 n 0 windowed hlp [n] can be causal

effect of phase and group delay of a linear system Given a narrowband input x[n]=s[n]cos(@n) for a system with frequency response H(ej), assume X(ej)is nonzero only around @=@ Around =@approximately, Group Delay arg[IH(eo]≈-4-ou, then t(@)-na it can be shown(see Problem5.63(二版5.57) that the responsey]to xIn]is MnHH(ei)s[n-nalcos(a(n-na) 0 the time delay of the envelope sIn]is n. -0 20
◆Given a narrowband input x[n]=s[n]cos(0n) for a system with frequency response H(e j ) , arg , ( ) 0 j H e nd − − ( ) nd then = it can be shown (see Problem 5.63(二版5.57)) that the response y[n] to x[n] is the time delay of the envelope s[n] is . nd Group Delay assume X(e j ) is nonzero only around =0 , effect of phase and group delay of a linear system 20 ( ) ( ) 0 0 0 [ ] cos( ) d j y n H e s n n n nd = − − − Around =0 , approximately

effect of phase and group delay of a linear system 0.5 narrowband input xn]=s n cos(@on 0.5 Sample number (n) 50 100 150 200 250 300 ◆for a system H(ei),arg[H(eo】≈-4-oa, Group Delay t(@)=n=125 0.5 0 -0.5 Output Sample number (n) 0 50 150 200 250 300 MnHH(eia)s[n-nalcos(a(n-na)) the time delay of the envelope sn]is n=125. 21
narrowband input x[n]=s[n]cos(0n) ( )= = nd 125 the time delay of the envelope s[n] is . nd =125 Group Delay effect of phase and group delay of a linear system 21 ◆for a system H(e j ), arg , ( ) 0 j H e nd − − ( ) ( ) 0 0 0 [ ] cos( ) d j y n H e s n n n nd = − − − Output

5.1.2 Illustration of Effects of Group Delay and Attenuation Consider the system having system function: (1-.98ej.8rz1)(1-98e-j.8rz-1) H() (1-.8ej.4πz-1)(1-.8e-j.4rz-1) 18阶,8个2重极点, H1(z) 2个单极点 4 (c陵-z-1)ck-z1)】 X k=1 (1-cz-1)1-c陵z1) H2(z)allpass system 2(z) with ck=0.95e(.15r+.02 k)for k=1,2,3,4 22
◆Consider the system having system function: 5.1.2 Illustration of Effects of Group Delay and Attenuation × H2 (z) allpass system 22 18阶, 8个2重极点, 2个单极点
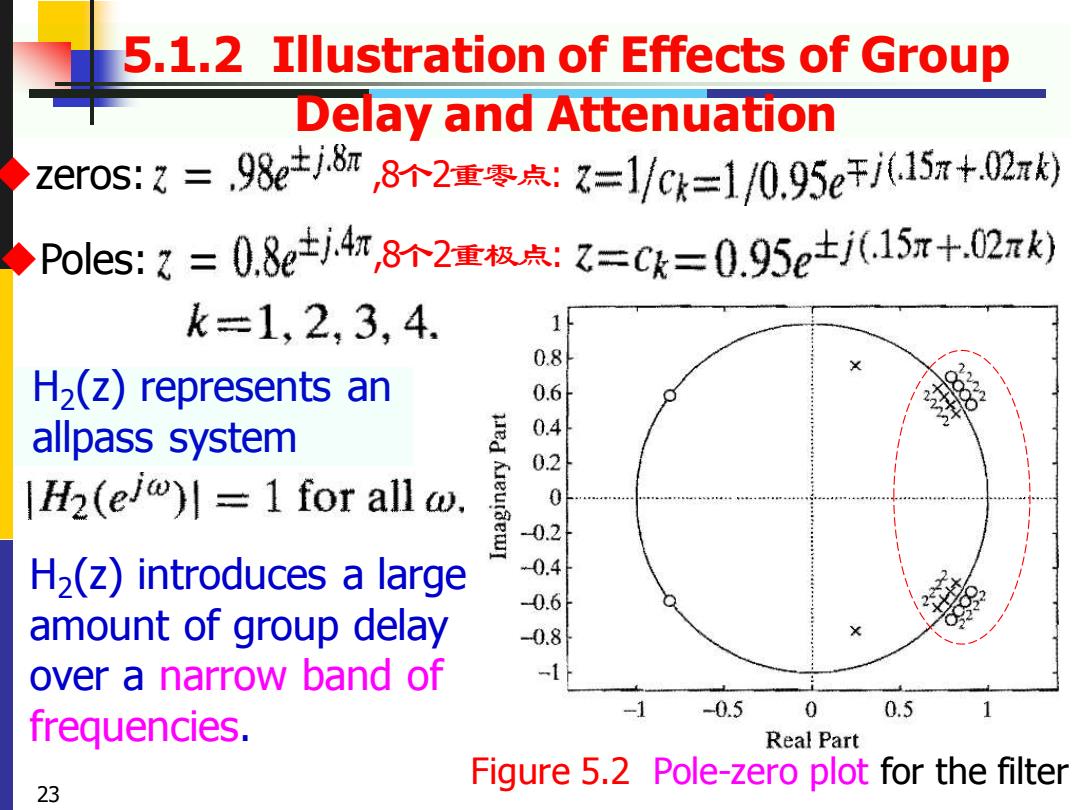
5.1.2 Illustration of Effects of Group Delay and Attenuation zeros:z=,98e±j8r,8个2重零点:z=1/c=1/0.95e干j15r+.02x利 >Poles:?=0.8ej,4杯,8个2重极点:z=ck=0.95e+j(.15r+.02x k=1,2,3,4. 1 0.8 H2(z)represents an 0.6 allpass system 0.4 0.2 H2(e/w)川=1 for all w. 0 0.2 H2(z)introduces a large -0.4 0.6 amount of group delay 0.8 over a narrow band of -1 -0.5 0 0.5 frequencies. Real Part Figure 5.2 Pole-zero plot for the filter 23
◆zeros: 5.1.2 Illustration of Effects of Group Delay and Attenuation Figure 5.2 Pole-zero plot for the filter H2 (z) represents an allpass system H2 (z) introduces a large amount of group delay over a narrow band of frequencies. 23 ◆Poles: ,8个2重零点: ,8个2重极点: