
5.1.1 Frequency Response Phase and Group Delay To understand the effect of the phase and the group delay of a linear system,first consider the ideal delay system: yn =xn-na. ◆The impulse response haln]=n-na The frequency response Hid(ej)-e jon H(el,∠Hna(eo)=-u,ll水k元 14
5.1.1 Frequency Response Phase and Group Delay hid n = n − nd n nd y n = x − ( ) d j j n H e e id − = ( ) 1, j H e id = ( ) , j H e n id d =− ◆The frequency response ◆The impulse response ◆To understand the effect of the phase and the group delay of a linear system, first consider the ideal delay system: 14

effect of phase and group delay of a linear system For ideal delay system:n Hid(eio)e-jon r(a)-farg(arge or =%{-om}, The constant group delay nrepresents a convenient measure of the linearity of the phase. The effect of constant group delay na for a system is to delay the input by n samples to get the output
effect of phase and group delay of a linear system ◆For ideal delay system: d d d n n d =− − = The constant group delay nd represents a convenient measure of the linearity of the phase. The effect of constant group delay nd for a system is to delay the input by nd samples to get the output . ( ) arg ( ) j id d H e d =−( ) d j j n H e e id − = , y n x n n = − d 15 arg d d j n d e − =− The constant group delay represents a convenient
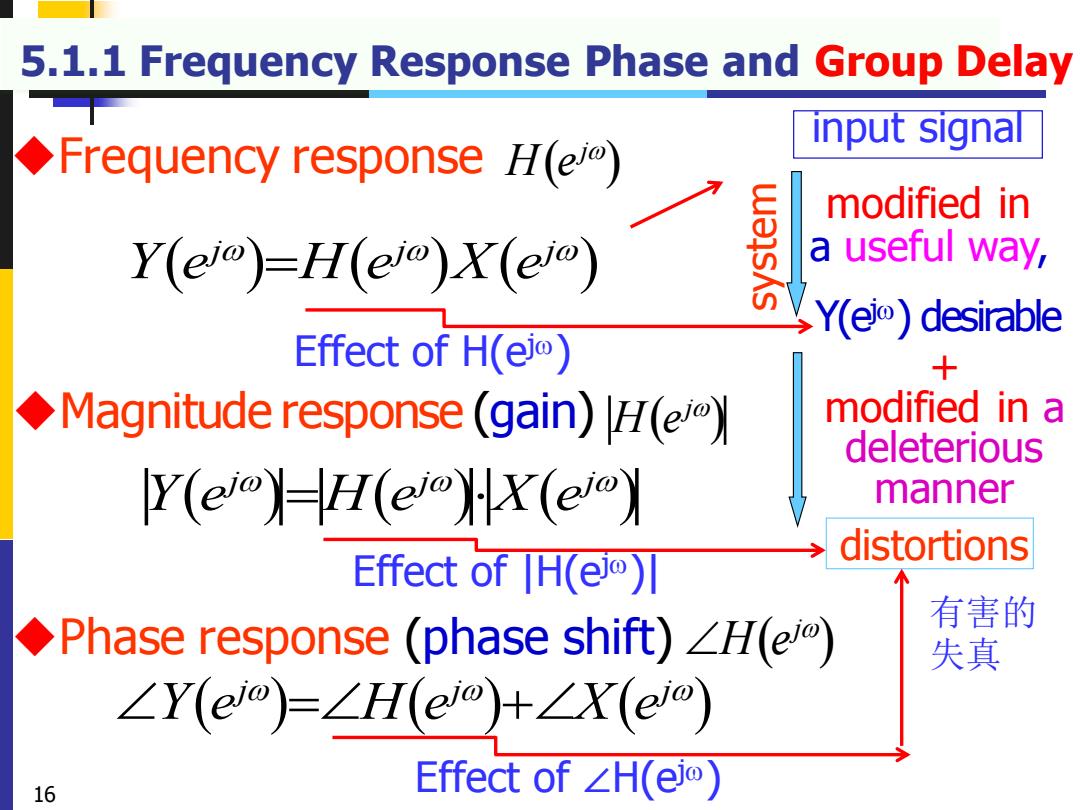
5.1.1 Frequency Response Phase and Group Delay input signal Frequency response H(el) modified in Y(eo)=lH(eo)X(em) a useful way, Ye)desirable Effect of H(ei) 十 Magnitude response (gain)H(ei) modified in a deleterious Y(ei-H(ei)X(e) manner distortions Effect of |H(eo刃 ◆Phase response(phase shift)∠H(eo) 有害的 失真 ∠Y(eo)=∠H(eo+∠X(eo) 16 Effect of∠H(eio)
5.1.1 Frequency Response Phase and Group Delay ( ) ( ) ( ) j j j Y e H e X e = ( ) ( ) ( ) j j j Y e H e X e = ◆Phase response (phase shift) ( ) H ej ( ) ( ) ( ) j j j Y e H e X e = + ( ) ◆ H ej Frequency response ( ) ◆Magnitude response H ej (gain) distortions modified in a useful way, system input signal 16 Y(e j) desirable + modified in a deleterious manner Effect of H(ej) Effect of |H(ej)| Effect of ∠H(ej) 有害的 失真

5.1.1 Frequency Response Phase and Group Delay delay distortion is a rather mild form of phase distortion,its effect is to shift the sequence in time. we accept a linear-phase response rather than a zero phase response in designing filters by method of approximations to ideal filters Ideal lowpass filter with linear phase delay is better ue-本2e四设apgn Hp(e) The impulse response(delayed by time nd) (sing( 元(n-nu -00<1n<00 Ht四相=9 windowed hpl[n]can be causal,,e.g.0≤n≤20,n=l0 17
5.1.1 Frequency Response Phase and Group Delay ◆Ideal lowpass filter with linear phase delay is better ( ) ,| | , 0, | | j c lp c d j n H e e − = ◆delay distortion is a rather mild form of phase distortion, ◆The impulse response (delayed by time nd ) its effect is to shift the sequence in time. 17 in designing filters by method of approximations to ideal filters . windowed hLP[n] can be causal, ( ) ( ) ( ) sin , c d lp d n h n n n n n − = − − we accept a linear-phase response rather than a zero phase response . . 0 20, 10 d e g = n n ( ) , | | 0, | | j 1 c lp c H e =

5.1.1 Frequency Response Phase and Group Dela Ideal lowpass filter (zero phase) e-ae生 e8 0,o4o昨元 linear phase a,-s1ng”,o<n< no phase distortion Infinite,computationally unrealizable 元n Noncausal,physically unrealizable sin@(n-na)oo<n<c windowed hp[n]can be causal, π(n-na) 1H(e) e.g.0≤n≤20,n=l0 -2π 0 π 2元 18
5.1.1 Frequency Response Phase and Group Delay ◆Ideal lowpass filter (zero phase) ( ) j H e − 2 − −c 0 c 2 1 sin , c lp n h n n = 18 − n k y n x k h n k =− = − windowed hlp[n] can be causal, . . 0 20, 10 d e g = n n •no phase distortion •Infinite, computationally unrealizable •Noncausal, physically unrealizable ( ) ,| | , 0, | | j c lp c d j n H e e − = ( ) ( ) ( ) sin , d d c lp n h n n n n − = − ( ) , | | , 0, | | j 1 c lp c H e = − n linear phase