
4、感应电动势 “方向”的再讨论 (1)为什么感应电动势的“方向”必须是楞 次定律所规定的? 这是能量守恒定律所要求的。 在前面的第二个实验中,当磁铁插入线圈时 穿过线圈的磁通量增加,按照楞次定律,感 应电流激发的磁通量应抵消原磁通量的改变 线圈将对磁棒产生一个排斥力,阻碍磁棒继 续往下插入。所以,要使感应电流连续不断, 侧外界必须克服这个排斥力对磁棒作功。因 此,线圈中感应电流的获得,即电能的获得, 是以消耗机械能为代价的
4、感应电动势 “方向”的再讨论 ■ (1)为什么感应电动势的“方向”必须是楞 次定律所规定的? 这是能量守恒定律所要求的。 ■ 在前面的第二个实验中,当磁铁插入线圈时, 穿过线圈的磁通量增加,按照楞次定律,感 应电流激发的磁通量应抵消原磁通量的改变, 线圈将对磁棒产生一个排斥力,阻碍磁棒继 续往下插入。所以,要使感应电流连续不断, 则外界必须克服这个排斥力对磁棒作功。因 此,线圈中感应电流的获得,即电能的获得, 是以消耗机械能为代价的

反之,假如感应电动势的“方向”与楞 次定律规定的方向相反,那末只要磁铁稍有 运动,在线圈中产生感应电流,这感应电流 产生的磁通就会增强这种变化,于是能连续 不断的产生感应电流,而不再消耗能量。这 是不可能的,因为它违背了能量守恒定律 所以,感应电动势的“方向”一定是楞 次定律规定的方向
反之,假如感应电动势的“方向”与楞 次定律规定的方向相反,那末只要磁铁稍有 运动,在线圈中产生感应电流,这感应电流 产生的磁通就会增强这种变化,于是能连续 不断的产生感应电流,而不再消耗能量。这 是不可能的,因为它违背了能量守恒定律。 所以,感应电动势的“方向”一定是楞 次定律规定的方向

(2)如何确立感应电动势的正负问题 电动势ε与磁通量Φ的正负都与回路的绕行 方向有关,所以,要讨论感应电动势和磁通量 的“方向”,首先要选定回路的绕行方向。绕 行方向选定后,若计算电动势为正值, 表明 电动势的“方向”与回路绕行的方向一致。反 之,则相反。 但必须强调,根据上述约定,不管开始时 选定怎样的绕行方向,应用法拉第定律得到的 感应电动势的“方向”和数值是唯一确定的 与回路绕行方向的选取无关。下面举例说明
(2)如何确立感应电动势的正负问题 n 电动势与磁通量的正负都与回路的绕行 方向有关,所以,要讨论感应电动势和磁通量 的“方向” ,首先要选定回路的绕行方向。绕 行方向选定后,若计算电动势为正值 ,表明 电动势的“方向”与回路绕行的方向一致。反 之,则相反。 n 但必须强调,根据上述约定,不管开始时 选定怎样的绕行方向,应用法拉第定律得到的 感应电动势的“方向”和数值是唯一确定的, 与回路绕行方向的选取无关。下面举例说明
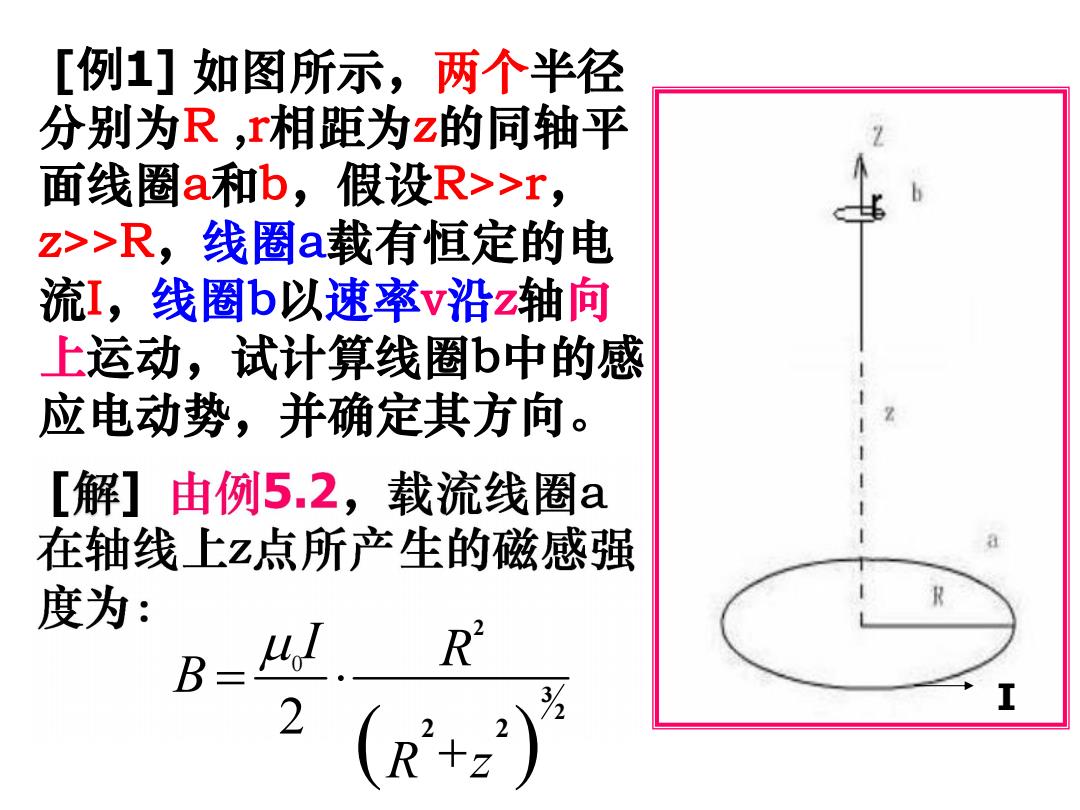
[例1]如图所示,两个半径 分别为R,r相距为z的同轴平 面线圈a和b,假设R>>r, z>>R,线圈a载有恒定的电 流I,线圈b以速率v沿z轴向 上运动,试计算线圈b中的感 应电动势,并确定其方向。 [解]由例5.2,载流线圈a 在轴线上z点所产生的磁感强 度为: B= 4I R 3 2 工 (R+z)
[例1] 如图所示,两个半径 分别为R ,r相距为z的同轴平 面线圈a和b,假设R>>r, z>>R,线圈a载有恒定的电 流I,线圈b以速率v沿z轴向 上运动,试计算线圈b中的感 应电动势,并确定其方向。 02 I R B R z2 32 2 2 I

B的方向沿Z轴的正方向,大小随Z变化。 由于z>>R,R>>r,所以在线圈b所围的 平面内,B可以近似看作均匀分布的。由于线 圈b沿Z轴正方向以速度V运动,因此通过线圈 b的磁通量发生变化,所以在线圈b中产生感应 电动势,从而产生感应电流。 下面我们选不同的回路绕行方向来计算感 应电动势:
B的方向沿Z轴的正方向,大小随Z变化。 由于z>>R, R >> r ,所以在线圈b所围的 平面内, B可以近似看作均匀分布的。由于线 圈b沿Z轴正方向以速度v运动,因此通过线圈 b的磁通量发生变化,所以在线圈b中产生感应 电动势,从而产生感应电流。 下面我们选不同的回路绕行方向来计算感 应电动势: