
第八章磁能 §8.1戴流线圈系统的磁能 §8.2戴流线圈在外磁场中的磁能 §8.3 磁场的能量和磁能密度 *§8.4非线性介质及磁滯损耗 *§8.5 利用磁能求磁力
第八章 磁能 §8.1 戴流线圈系统的磁能 §8.2 戴流线圈在外磁场中的磁能 §8.3 磁场的能量和磁能密度 *§8.4 非线性介质及磁滯损耗 *§8.5 利用磁能求磁力
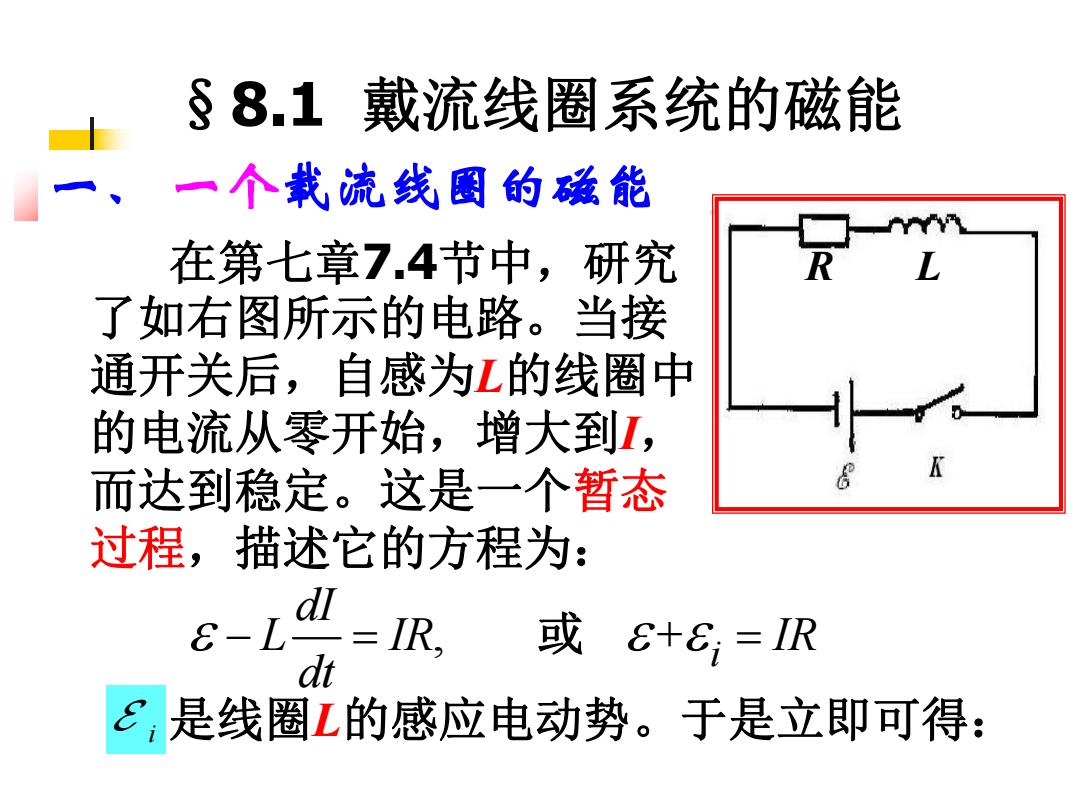
§8.1戴流线圈系统的磁能 一个载流线图的磁能 在第七章7.4节中,研究 R 了如右图所示的电路。当接 通开关后,自感为L的线圈中 的电流从零开始,增大到I, 而达到稳定。这是一个暂态 过程,描述它的方程为: dl -L=IR, 或&+E=IR dt ,是线圈L的感应电动势。于是立即可得:
§8.1 戴流线圈系统的磁能 一 、 一个载流线圈的磁能 在第七章7.4节中,研究 了如右图所示的电路。当接 通开关后,自感为L的线圈中 的电流从零开始,增大到I, 而达到稳定。这是一个暂态 过程,描述它的方程为: R L , + i dI L IR IR dt 或 i 是线圈L的感应电动势。于是立即可得:

Idt =i LIdI +I-Rdt (8.1.1) 或 8Idt =-8 Idt+I'Rdt (8.1.2) ■式(8.1.1)说明,电源在时间dt内作功并消耗能 量SIdi, 其中除一部分转变为电阻R的焦耳热I2Rdt 之外,另一部分用来反抗线圈的感应电动势作功,其 值为Lldl或-&,Idt。 ■我们知道,在开关接通以前线圈中的电流为零,其 磁场为零,作为零能态;开关接通后,电流逐渐增大, 线圈内磁场逐渐增强,这正是电源消耗一部分能量反 抗线圈的感应电动势作功的结果,该能量转变为线圈 的磁能(即磁场能)W
Idt LIdI I Rdt 2 或 2 i Id t Id t I R d t (8.1.1) (8.1.2) ■式(8.1.1)说明,电源在时间 内作功并消耗能 量 ,其中除一部分转变为电阻R的焦耳热 之外,另一部分用来反抗线圈的感应电动势作功,其 值为 或 。 ■我们知道,在开关接通以前线圈中的电流为零,其 磁场为零,作为零能态;开关接通后,电流逐渐增大, 线圈内磁场逐渐增强,这正是电源消耗一部分能量反 抗线圈的感应电动势作功的结果,该能量转变为线圈 的磁能(即磁场能) : dt Idt 2 I Rdt LIdI Wm i Idt
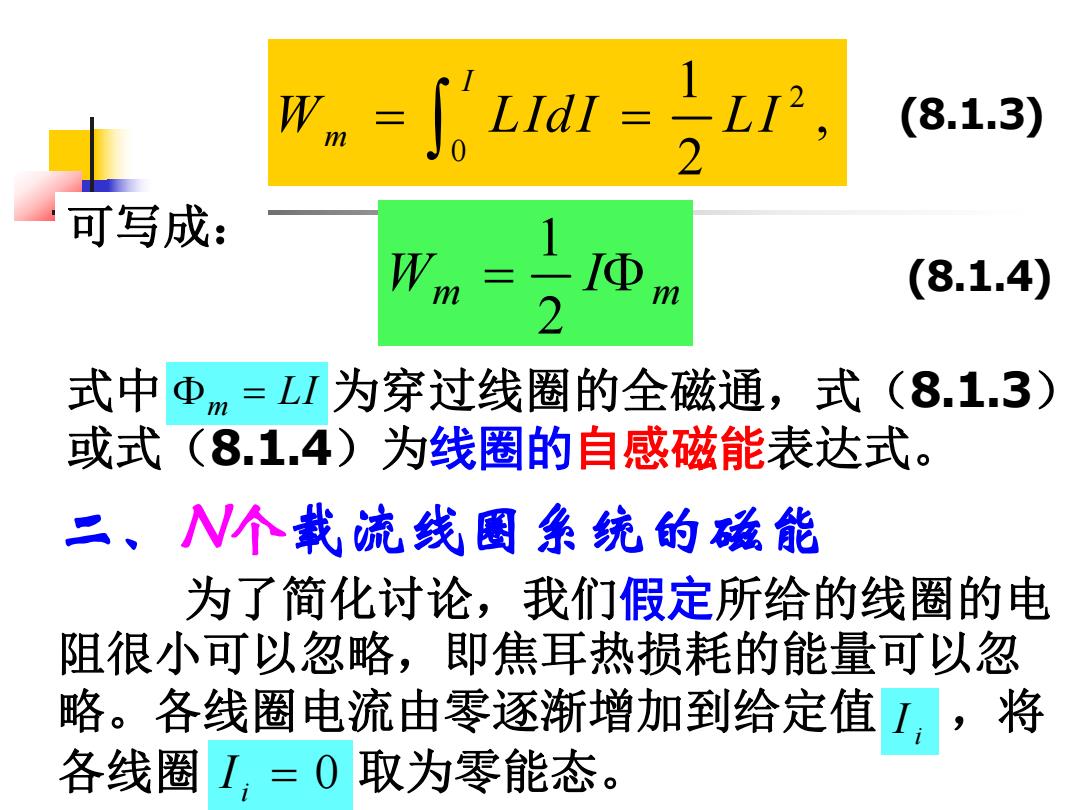
R。-ia=, (8.1.3) 可写成: m (8.1.4) 2 式中Φm=L1为穿过线圈的全磁通,式(8.1.3) 或式(8.1.4)为线圈的自感磁能表达式。 二、N个载流线图条统的強能 为了简化讨论,我们假定所给的线圈的电 阻很小可以忽略,即焦耳热损耗的能量可以忽 略。各线圈电流由零逐渐增加到给定值,,将 各线圈1,=0取为零能态
2 0 1 , 2 I Wm LIdI LI (8.1.3) 可写成: Wm Im 2 1 (8.1.4) 式中 为穿过线圈的全磁通,式(8.1.3) 或式(8.1.4)为线圈的自感磁能表达式。 m LI 二、N个载流线圈系统的磁能 为了简化讨论,我们假定所给的线圈的电 阻很小可以忽略,即焦耳热损耗的能量可以忽 略。各线圈电流由零逐渐增加到给定值 ,将 各线圈 取为零能态。 i I 0 i I

■ 在某一瞬间,在第个线圈中,感应电动势, 由下式确定: =-4-2w (8.1.5) dt k=1 dt k丰i L是第个线圈的自感, M H 是第k个线圈和第i 个线圈之间的互感。 ■因此,在第个线圈中, 电源反抗感应电动势£ 在t时间内所作的功是: W dj =-8 di ll dl,+ul dix (8.1.6) k=1 k≠i
■ 在某一瞬间,在第i个线圈中,感应电动势 由下式确定: i 1 N i k i i ki k k i dI dI L M dt dt (8.1.5) 是第i个线圈的自感, 是第k个线圈和第 i 个线圈之间的互感。 ■ 因此,在第i个线圈中,电源反抗感应电动势 在 dt 时间内所作的功是: L i M ki i N k i k i i i i i i ki i k dA I dt L I dI M I dI 1 (8.1.6)