
(a)选取线圈b的绕行方向为逆时针方向 由右手螺旋法则定S的法线的方向,现应为z轴的正 方向,与通过线圈b的磁场B同方向,通过b的磁通量 为: -B内=∬a=Bar- πr>O 2(R+) 因为z>>R,得到: 2 2 Z
(a)选取线圈b的绕行方向为逆时针方向 n 由右手螺旋法则定S的法线n的方向,现应为z轴的正 方向,与通过线圈b的磁场B同方向,通过b的磁通量 为: 因为z>>R,得到: 2 0 2 3 2 2 2 2 0 2 s s I R d BdS B r r R z B S r z R 2 I 2 3 2 0 I

根据法拉第电磁感应定律求得感应电动势为: dΦ_人 3πto IR r'dz dt ) 2 2z4 dt dz v,.,g= 3πuIR2r2 dt 2z4 因为ε>0,所以感应电流I的方向与回路的绕行方向 一致,即逆时针方向
根据法拉第电磁感应定律求得感应电动势为: 因为>0,所以感应电流I的方向与回路的绕行方向 一致,即逆时针方向。 dt dz z IR r dt z d R r I dt d 2 1 3 2 4 2 2 0 3 0 2 2 2 2 0 4 3 , 2 dz IR r v v dt z

(b)选取线倦的绕行方向为顺时针方向 这时S的法向n与B的方向相反,于是通过线圈b的磁 通量为: D (R2+Z2) <0 2 于是: dΦ 3π4。IR2r2 dt 因为ε〈0,所以感应电流的方向与选定的回路b的绕 行方向相反,即沿逆时针方向,结果与(a)相同
(b)选取线圈b的绕行方向为顺时针方向 n 这时S的法向n与B的方向相反,于是通过线圈b的磁 通量为: 于是: n 因为 < 0 ,所以感应电流的方向与选定的回路b的绕 行方向相反,即沿逆时针方向,结果与(a)相同。 2 0 2 3 2 2 2 0 2 ( ) I R r R Z 2 2 0 4 3 0 2 d IR r v dt z

本例题表明,为了在解题过程中 计算通过回路的磁通量和考虑电动势 的“方向”,必须先选定回路的绕行 方向作为参考方向,但应用法拉第定 律得到的感应电动势大小和“方向” 是唯一确定的,与回路方向的选定无关
n 本例题表明,为了在解题过程中 计算通过回路的磁通量和考虑电动势 的“方向” ,必须先选定回路的绕行 方向作为参考方向,但应用法拉第定 律得到的感应电动势大小和“方向” 是唯一确定的,与回路方向的选定无关
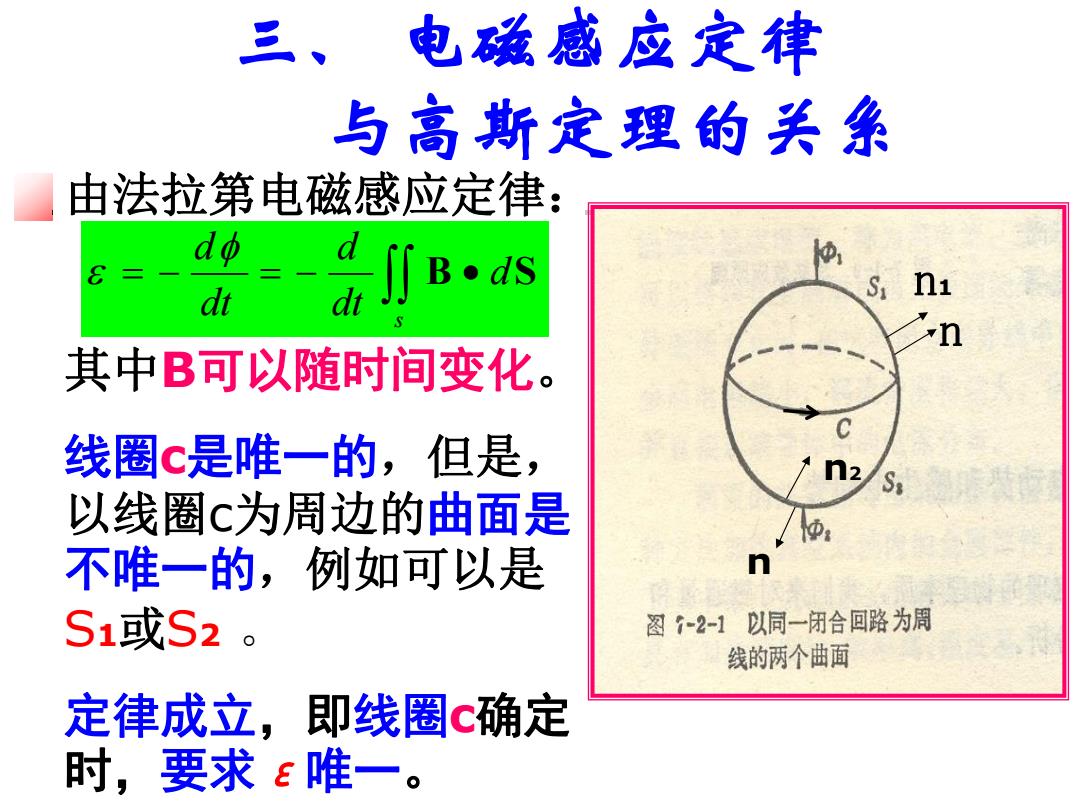
三、 电磁感应定律 与高斯定理的关系 由法拉第电磁感应定律 其中B可以随时间变化。 线圈c是唯一的,但是, 以线圈c为周边的曲面是 不唯一的,例如可以是 S1或S2。 图~2-1以同一闭合回路为周 线的两个曲面 定律成立,即线圈c确定 时,要求e唯一
三、 电磁感应定律 与高斯定理的关系 由法拉第电磁感应定律: 其中B可以随时间变化。 线圈c是唯一的,但是, 以线圈c为周边的曲面是 不唯一的,例如可以是 S1或S2 。 定律成立,即线圈c确定 时,要求ε唯一。 B dS dt d dt d s n1 n n2 n