2.2.2鲍林(Pauling)规则1-不同直径球堆积 Na+ 鲍林第一规则(配位多面体规则):“在离子晶体中,在正离子 周围形成一个负离子多面体,正负离子之间的距离取决于离子半 径之和,正离子的配位数取决于离子半径比
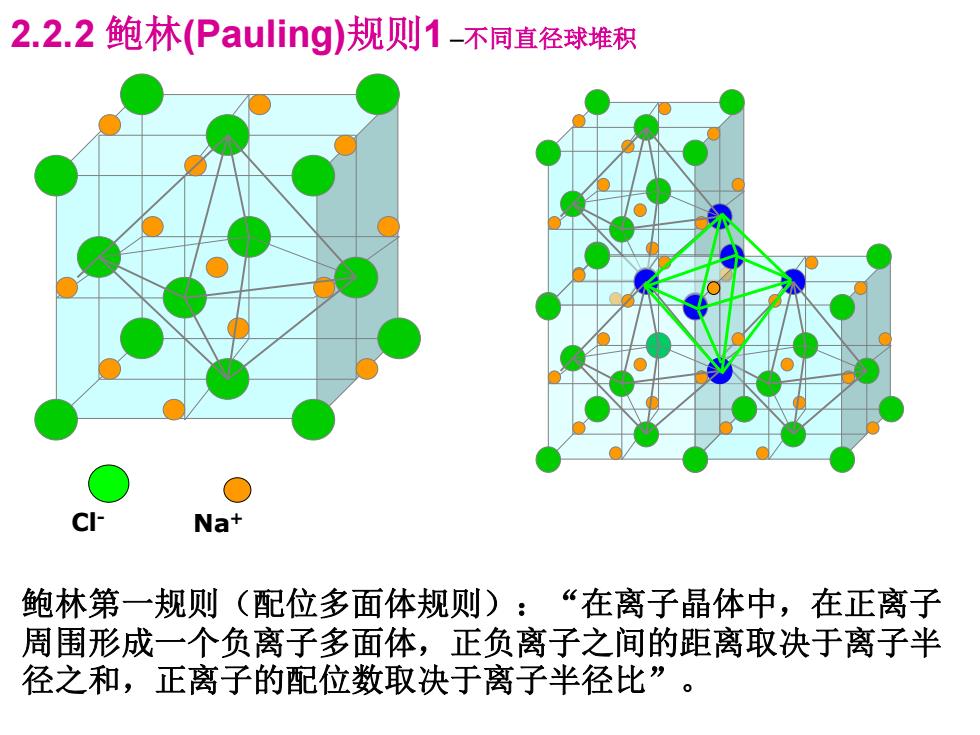
2.2.2 鲍林(Pauling)规则1 –不同直径球堆积 Cl- Na+ 鲍林第一规则(配位多面体规则):“在离子晶体中,在正离子 周围形成一个负离子多面体,正负离子之间的距离取决于离子半 径之和,正离子的配位数取决于离子半径比
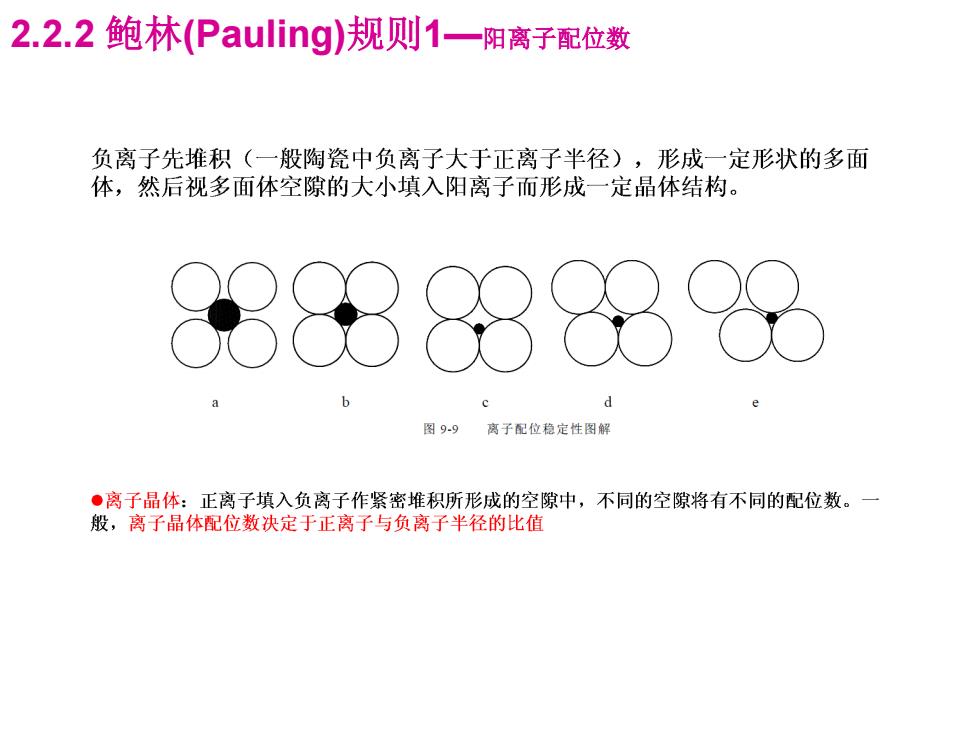
2.2.2鲍林(Pauling)规则1一阳离子配位数 负离子先堆积(一般陶瓷中负离子大于正离子半径),形成一定形状的多面 体,然后视多面体空隙的大小填入阳离子而形成一定晶体结构。 8886没 图99离子配位稳定性图解 ·离子品体:正离子填入负离子作紧密堆积所形成的空隙中,不同的空隙将有不同的配位数。一 般,离子晶体配位数决定于正离子与负离子半径的比值
2.2.2 鲍林(Pauling)规则1—阳离子配位数
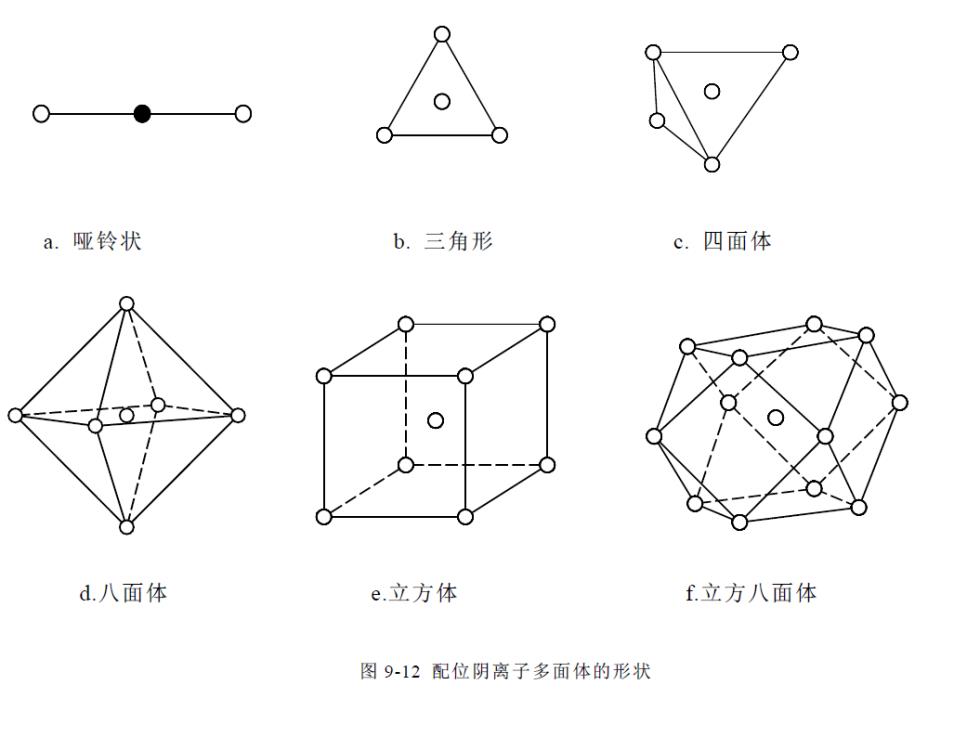
a.哑铃状 b.三角形 c.四面体 d.八面体 e立方体 f立方八面体 图9-12配位阴离子多面体的形状

四面体配位,阳离子半径求解 对于四面体配位,用立方体辅助图形来计算其半径比下限,如图9-10,立方体 六个面对角线构成一个正四面体,立方体中心就是四面体中心。如果立方体边长为, 则从四面体中心到顶点的距离为√5/2a,【a应是正四面体边长的一半,即√2/2a,这 样阴离子构成的空隙内能够容纳的阳离子的半径为: re=(5/2)a-(√/2)a r./ra=(5/2)a-(√5/2)a/(√/2)a =√5-√2/√2=0.225。 0.225就是配位数为4时(四面体配位),晶体结构保持稳定的阳离子和阴离子 的半径比下限。 图9-10四面体空隙阳、阴离子半径比下限求解
四面体配位,阳离子半径 求解
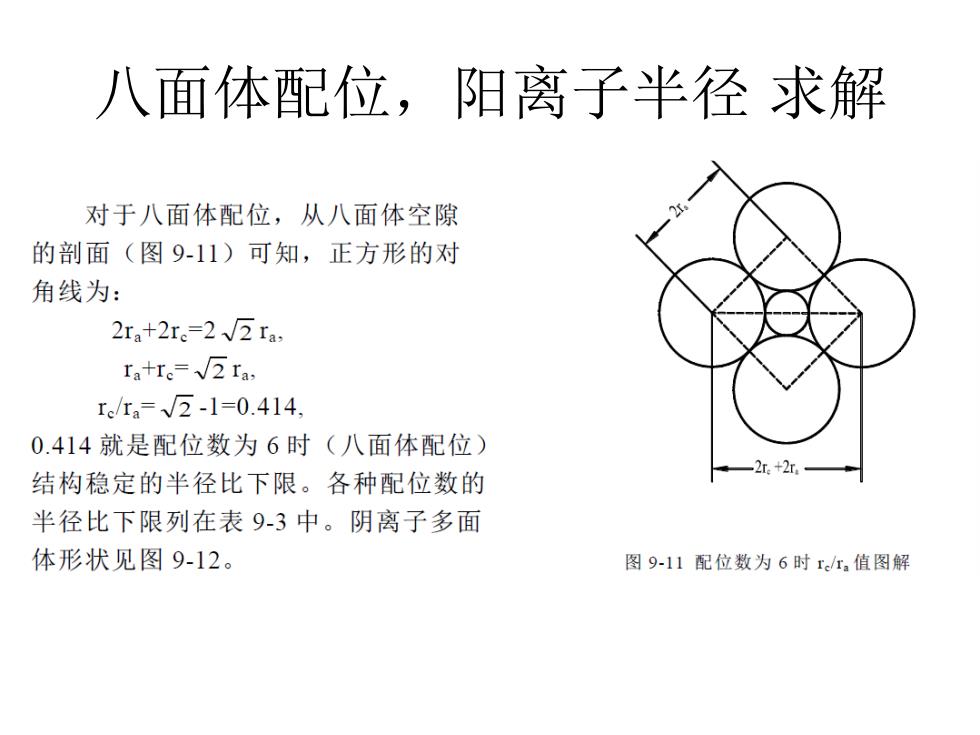
八面体配位,阳离子半径求解 对于八面体配位,从八面体空隙 的剖面(图9-11)可知,正方形的对 角线为: 2ra+2r.=2√2ra ra+r。=√2Ia, rc/ra=√2-1=0.414 0.414就是配位数为6时(八面体配位) 2红+2 结构稳定的半径比下限。各种配位数的 半径比下限列在表9-3中。阴离子多面 体形状见图9-12。 图9-11配位数为6时r,值图解
八面体配位,阳离子半径 求解