
相乘器输出: cos[@t+△0(tt+0+0t]cos@t仕△0(t)t+02+0t)] £,滤波器输出: 2os@-own1+6-01-o2mt+ay+/++0-4阴 f+△f cosf2(f,+qt+0,-0] 经q次分频输出:acos2π(f△f+0,] 二次相乘再取差频,经窄带滤波器输出: 1/2{a cos[wct+-△o(t)t+θt)+02-0,J]} 消除固定相移[0c(02-0】,就可获得所需相干载波。 12
12 相乘器输出: cos[ω1 t+△ω(t)t+θ1+θ(t)]cos[ω2 t+△ω(t)t+θ2+θ(t)] f 1 -f 2滤波器输出: cos[2 ( ) ] 2 1 cos[2 ( )(1 ) ] 2 1 cos[( ) ] 2 1 2 2 1 2 1 2 1 2 1 2 1 2 = + + − + − + + − + − = + + f f qt t f f f f t f f r r m r 经q次分频输出: a cos[2π(fr +△f 2 )t+θq ] 二次相乘再取差频,经fC窄带滤波器输出: 1/2{a cos[ωC t+△ω(t)t+θ(t)+θ2 -θq ]} 消除固定相移[θC -(θ2 -θ1 )],就可获得所需相干载波

二、直接法 1.Ψ方变换法和Ψ方换法 ()平方变换法 输入已调 e(t) 2f6 载波输出 平方律部件 窄带滤波器 二分频 信号 (os(co20 13
13 二、直接法 1.平方变换法和平方换法 (1)平方变换法 平方律部件 窄带滤波器 二分频 输入已调 信号 e t( ) 2 f c 载波输出 2 2 2 2 ( ) 1 ( ) ( )cos ( )cos 2 2 2 c c m t e t m t t m t t = = +
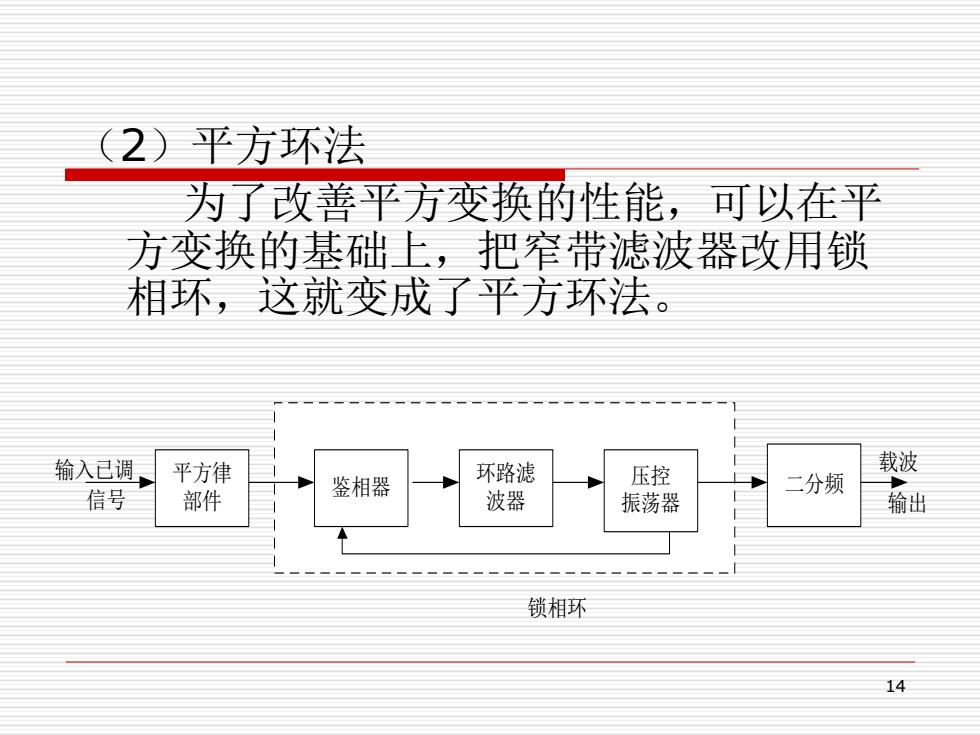
(2)平方环法 为了改善平方变换的性能,可以在平 方变换的基础上,把窄带滤波器改用锁 相环,这就变成了平方环法。 输入已调 平方律 环路滤 压控 载波 信号 部件 鉴相器 波器 二分频 振荡器 输出 锁相环 14
14 (2)平方环法 为了改善平方变换的性能,可以在平 方变换的基础上,把窄带滤波器改用锁 相环,这就变成了平方环法。 输入已调 平方律 部件 鉴相器 环路滤 波器 二分频 锁相环 信号 载波 输出 压控 振荡器

(3)关于相位模糊问题的讨论 由2f窄带滤波器得到的是cos2wt经过 三分频以后得到的可能是cosw t也可能是 cos(Wt+)。这种相位的不确定性称为相 位模糊。 相位模糊对模拟系统影响不大,但对 数字系统相位不同将使解调后码元反相, 对于2PSK信号可能出现“反相工作”问题, 因此要采用2DPSK系统。 15
15 (3)关于相位模糊问题的讨论 由2fc窄带滤波器得到的是cos2wc t经过 二分频以后得到的可能是coswc t也可能是 cos(wc t+π)。这种相位的不确定性称为相 位模糊。 相位模糊对模拟系统影响不大,但对 数字系统相位不同将使解调后码元反相, 对于2PSK信号可能出现“反相工作”问题, 因此要采用2DPSK系统
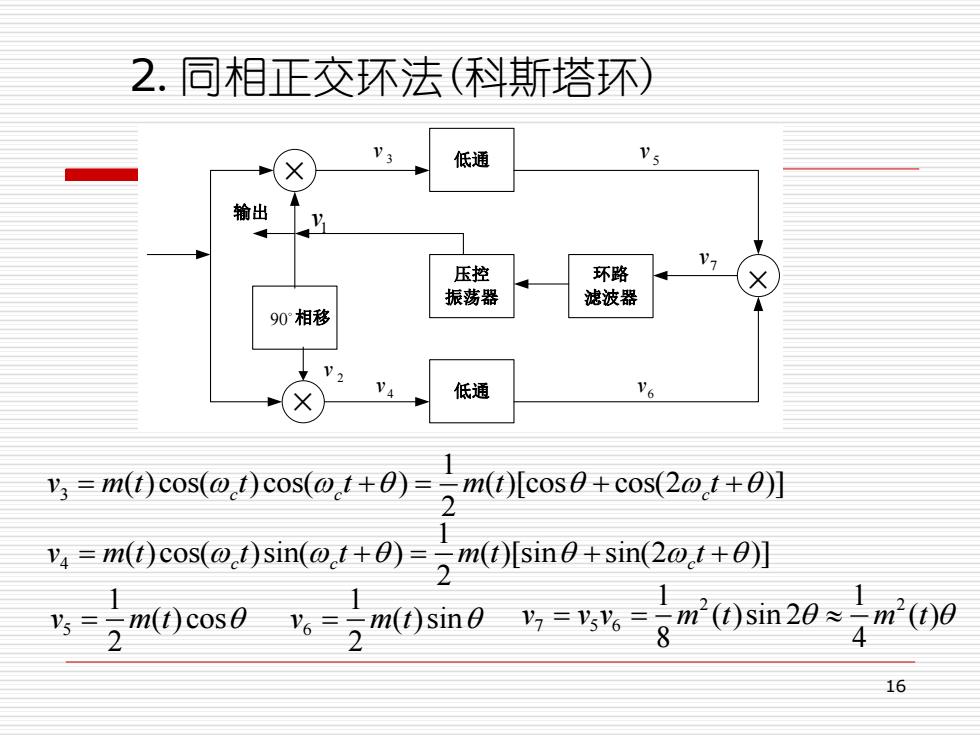
2.同相正交环法(科斯塔环) V3 低通 输出 压控 环路 V7 振荡器 滤波器 90相移 V4 低通 1 3=m(tcos(ot)cos(ot+θ)=-m(t儿cos0+cos(2o.t+θ)] ) ,m()cos()sin(m()sinsin(2) Ys=m(t)cose Ys=m()sine v=vsys=m(1)sin20m(1)0 16
16 2.同相正交环法(科斯塔环) 低通 相移 压控 振荡器 环路 滤波器 低通 1v 2 v 3 v 4 v 5 v 6 v 7 v 90 输出 3 1 ( )cos( )cos( ) ( )[cos cos(2 )] 2 c c c v m t t t m t t = + = + + 4 1 ( )cos( )sin( ) ( )[sin sin(2 )] 2 c c c v m t t t m t t = + = + + 5 1 ( )cos 2 v m t = 6 1 ( )sin 2 v m t = 2 2 7 5 6 1 1 ( )sin 2 ( ) 8 4 v v v m t m t = =