
山多够源宇花 参HANXI INSTITUT老OF ENEROY 3.热边界条件有均匀壁温和均匀热流两种 湍流:除液态金属外,两种条件的差别可不计 层流:两种边界条件下的换热系数差别明显。 入口段,充分发展段 t.(x) t4(x) tw一t4=const (x) =const q.=const (b) (a) 图6-4 均匀热流与均匀壁温条件下流体温度及 壁面温度沿主流方向的变化 6
6 3. 热边界条件有均匀壁温和均匀热流两种。 湍流:除液态金属外,两种条件的差别可不计 层流:两种边界条件下的换热系数差别明显。 图6-4

山色够源宇花 SHANXI INSTITUTE OF ENEROY 常热流边界条件下: dt; 2q -const dx PCpumR 故,常热流边界条件下,全管长的平均温度可取为进出口断面流 体平均温度的算术平均值 1,=G+/2 在热充分发展段有: dt const d dx 故,常热流边界条件下,全管长的流体与管壁间的对流换热传热 温差,可取为进出口温度差的算术平均值 At =(Ai+Al)2 7
7 const c u R q dx dt p m f = = 常热流边界条件下: 2 故,常热流边界条件下,全管长的平均温度可取为进出口断面流 体平均温度的算术平均值 ( ) 2 ' " f f f t = t +t 在热充分发展段有: const dx dt dx dt f w = = 故,常热流边界条件下,全管长的流体与管壁间的对流换热传热 温差,可取为进出口温度差的算术平均值 ( ) 2 ' " t = t +t

山西破源宇花 SHANXI INSTITUTE OF ENEROY 常壁温边界条件下: d,2h.6。-t),dl。-t) 2h,dx dx pcpumR (tv-tr)pcpumR 两侧沿管长由0到x积分得 2hx = t.-t, exp PCpumR 故,常壁温边界条件下,流体与壁面间的温度差将沿管长按对数曲线 规律变化。进一步推导,可得全管长流体与壁面间的平均温度差: 6.-i)-(.-t)△i-△ △tnm △i 8
8 常壁温边界条件下: ( ) ( ) ( ) c u R h dx t t d t t c u R h t t dx dt p m x x w f x w f p m x f x w f 2 2 = − − − − = 两侧沿管长由0到x积分得 = − − − c u R hx t t t t w p m w f f 2 exp ' " 故,常壁温边界条件下,流体与壁面间的温度差将沿管长按对数曲线 规律变化。进一步推导,可得全管长流体与壁面间的平均温度差: ( ) ( ) " ' ' " " ' ' " ln ln t t t t t t t t t t t t t w f w f w f w f m − = − − − − − =

山西限源宇院 HANXI IN台TITUT老OF ENEROY 二.管内湍流换热实验关联式 实用上使用最广的是迪贝斯一贝尔特公式: Nu 0.023 Re8 Pr2 加热流体时n=0.4,冷却流体时n=0.3。 式中定性温度采用流体平均温度t,特征长度为 管内径。 实验验证范围:Re,=104~1.2x10,Pr,=0.7~120, 1/d≥60。 此式适用与流体与壁面具有中等以下温差场合。 9
9 二. 管内湍流换热实验关联式 实用上使用最广的是迪贝斯-贝尔特公式: 加热流体时 ,冷却流体时 。 式中定性温度采用流体平均温度 ,特征长度为 管内径。 实验验证范围: 此式适用与流体与壁面具有中等以下温差场合。 = 0.8 0.023 Re Prn f f f N u n = 0.4 n = 0.3 f t = 4 5 Re 10 ~ 1.2 10 , f P r 0 . 7 ~ 1 2 0, = f l d / 6 0
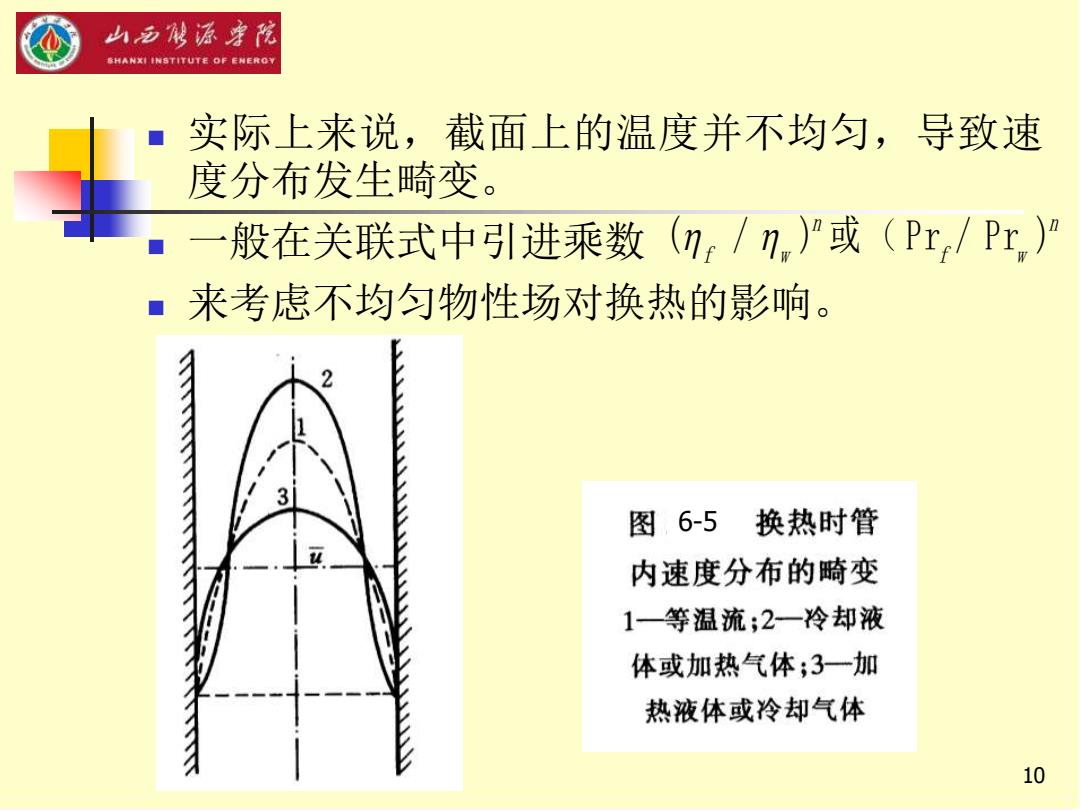
山西城源宇院 参HANXI INSTITUT老OF ENEROY 实际上来说,截面上的温度并不均匀,导致速 度分布发生畸变 一般在关联式中引进乘数 (n/n,或(Pr/Pr)A ■来考虑不均匀物性场对换热的影响。 图,6-5换热时管 内速度分布的畸变 1一等温流;2一冷却液 体或加热气体;3一加 热液体或冷却气体 10
10 ◼ 实际上来说,截面上的温度并不均匀,导致速 度分布发生畸变。 ◼ 一般在关联式中引进乘数 ◼ 来考虑不均匀物性场对换热的影响。 ( / ) Pr / Pr ) 或 ( n n f w f w 6-5