
Paths Consider a flow graph G=(N,E).A sequence of k edges,k >0, (e_1,e_2,...,e_k),denotes a path of length k through the flow graph if the following sequence condition holds. > Given that np,ng,nr,and ns are nodes belonging to N,and O<i<k,if ei=(np,na)and ei+1=(nr,ns)then ng nr Complete path:a path from start to exit Subpath:a subsequence of a complete path 11
11 Paths • Consider a flow graph G = (N, E). A sequence of k edges, k >0, (e_1,e_2,…,e_k), denotes a path of length k through the flow graph if the following sequence condition holds. ➢ Given that 𝑛𝑝, 𝑛𝑞, 𝑛𝑟 , and 𝑛𝑠 are nodes belonging to N, and 0<i<k, if 𝑒𝑖 = (𝑛𝑝, 𝑛𝑞) and 𝑒𝑖+1 = (𝑛𝑟 , 𝑛𝑠 ) then 𝑛𝑞 = 𝑛𝑟 ➢ Complete path: a path from start to exit ➢ Subpath: a subsequence of a complete path
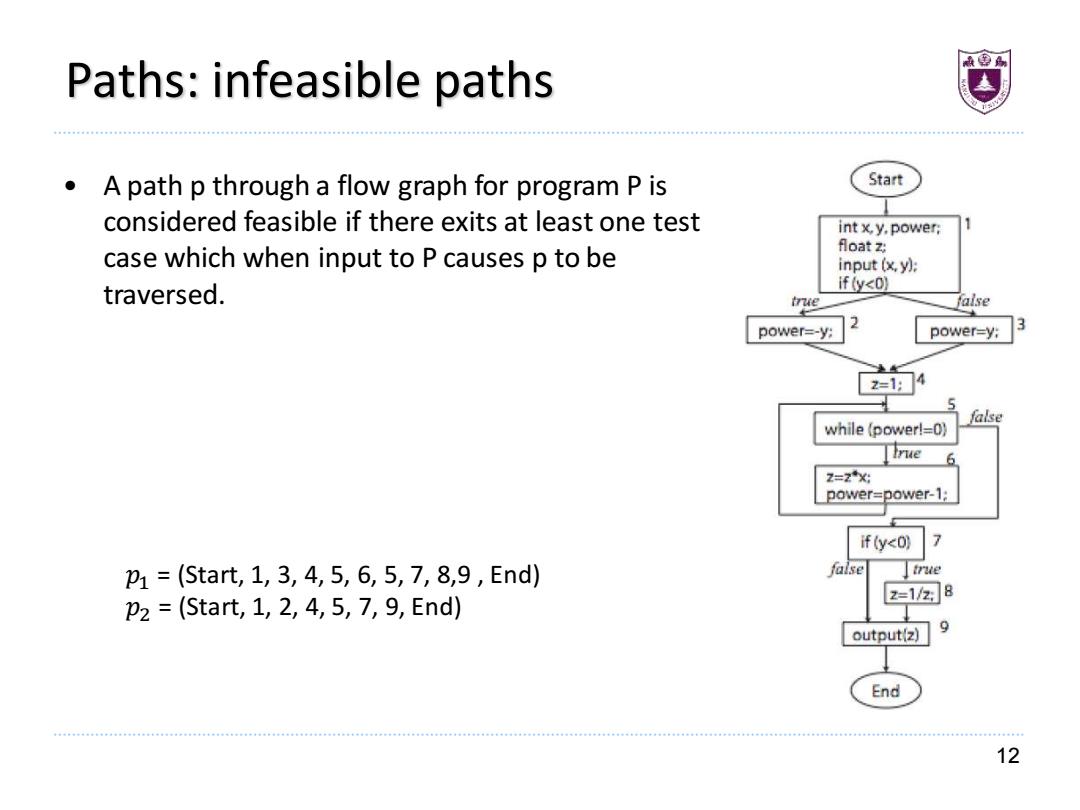
Paths:infeasible paths A path p through a flow graph for program P is Start considered feasible if there exits at least one test int x,y.power: case which when input to P causes p to be floatZ input(仪y: traversed. if (y<0) true false power=-y: power-y: 3 214 false while (power!=0) true 6 2=2X power=power-1: if (y<0) 7 P1=(Start,1,3,4,5,6,5,7,8,9,End) false Itrue p2=(Start,1,2,4,5,7,9,End) 2=128 output(z) 9 End 12
12 Paths: infeasible paths • A path p through a flow graph for program P is considered feasible if there exits at least one test case which when input to P causes p to be traversed. 𝑝1 = (Start, 1, 3, 4, 5, 6, 5, 7, 8,9 , End) 𝑝2 = (Start, 1, 2, 4, 5, 7, 9, End)

Number of paths There can be many distinct paths through a program.A program with no condition contains exactly one path that begins at node Start and terminates at node End. ● Each additional condition in the program can increase the number of distinct paths by at least one. Depending on their location,conditions can have a multiplicative effect on the number of paths. 13
13 Number of paths • There can be many distinct paths through a program. A program with no condition contains exactly one path that begins at node Start and terminates at node End. • Each additional condition in the program can increase the number of distinct paths by at least one. • Depending on their location, conditions can have a multiplicative effect on the number of paths
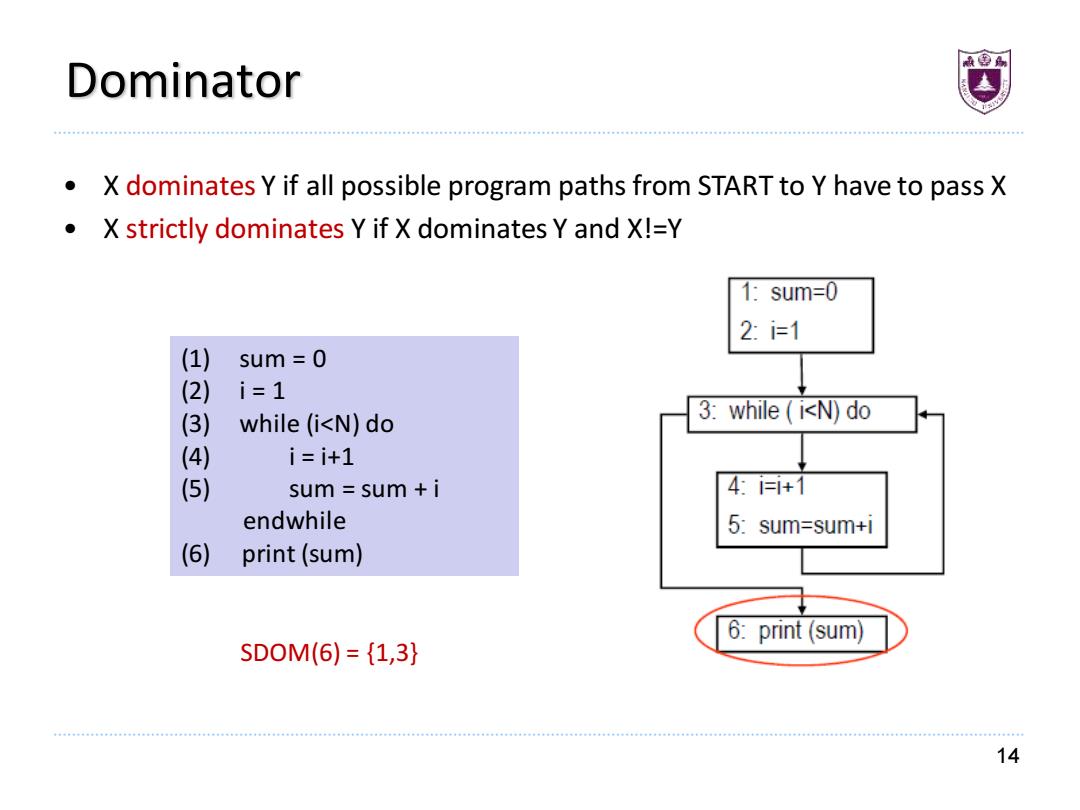
Dominator ● X dominates Y if all possible program paths from START to Y have to pass X X strictly dominates Y if X dominates Y and X!=Y 1:sum=0 2:i=1 (1) sum=0 (2) i=1 (3) while (i<N)do 3:while (i<N)do (4) i=i+1 (5) sum sum +i 4:=+1 endwhile 5: sum=sum+I (6) print(sum) 6:print (sum) SD0M(6)={1,3} 14
14 Dominator • X dominates Y if all possible program paths from START to Y have to pass X • X strictly dominates Y if X dominates Y and X!=Y (1) sum = 0 (2) i = 1 (3) while (i<N) do (4) i = i+1 (5) sum = sum + i endwhile (6) print (sum) SDOM(6) = {1,3}
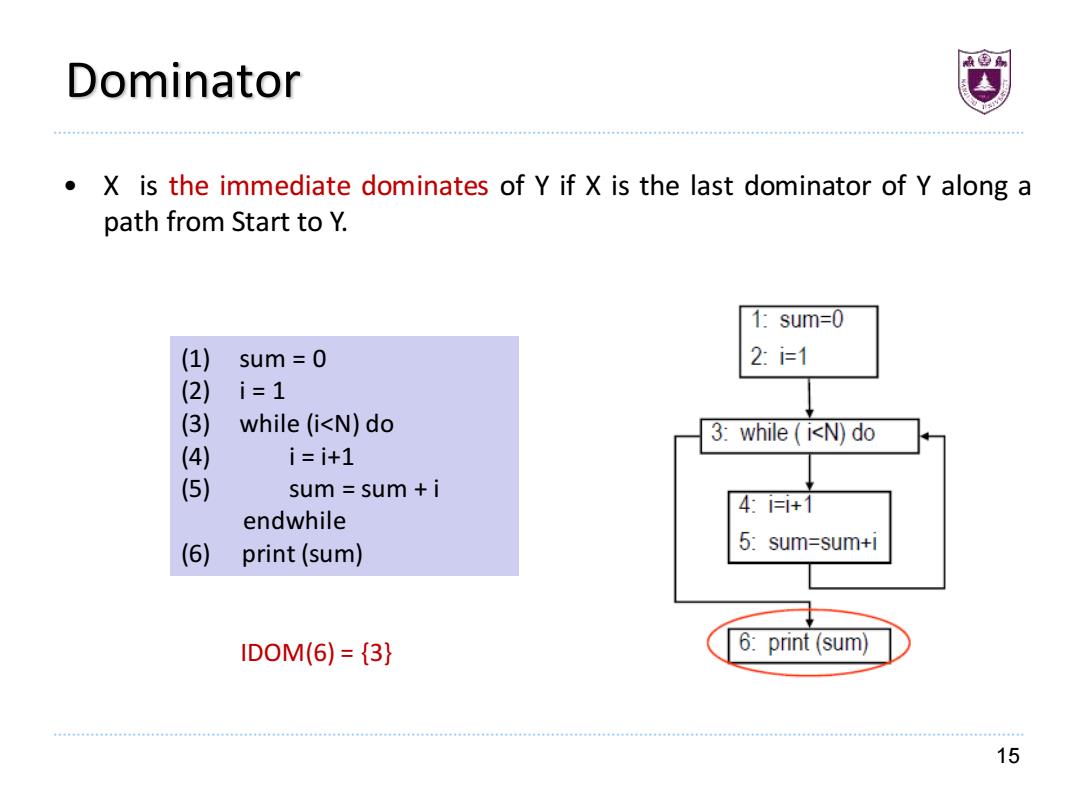
Dominator X is the immediate dominates of Y if X is the last dominator of Y along a path from Start to Y. 1:sum=0 (1) sum=0 2:i=1 (2) i=1 (3) while (i<N)do 3:while i<N)do (4) i=i+1 (5) sumsum +i 4:1+1 endwhile (6) print(sum) 5:sum=sum+i ID0M(6)={3} 6:print (sum) 15
15 Dominator • X is the immediate dominates of Y if X is the last dominator of Y along a path from Start to Y. (1) sum = 0 (2) i = 1 (3) while (i<N) do (4) i = i+1 (5) sum = sum + i endwhile (6) print (sum) IDOM(6) = {3}