电子科技大学：《现代网络理论与综合 Theory and Synthesize of Electric Network》研究生课程教学资源（课件讲稿）第19讲 有源滤波器综合基础（有源滤波器）

2 RC网络容易设计。 3 RC u 十 常用桥型网络： Vo Y 1 4 3 Y Y Y 2

RC网络容易设计。 常用桥型网络： ui uo      RC 1 3 2 Y3 Y4 Y2 Y1 4 1 2 3

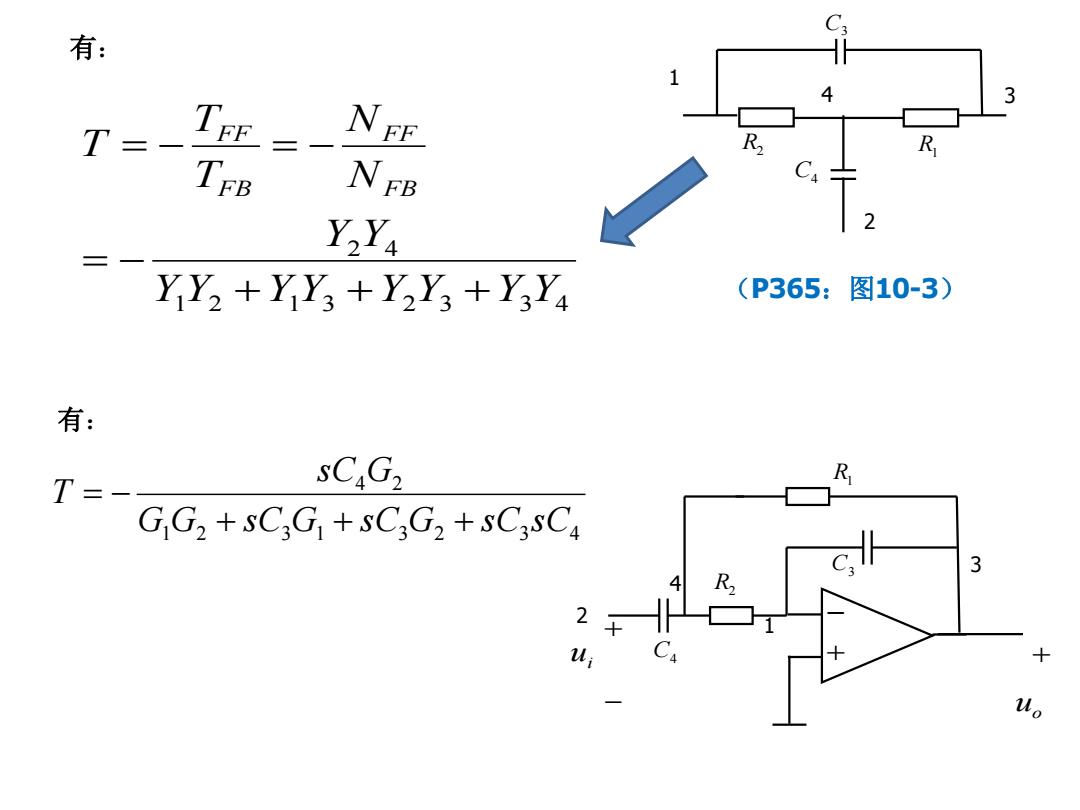
有： 4 T=- =- EE R TFB EB Y,Ya 2 YY+yYs+yYs+YsYa (P365:图10-3) 有： R T sCaG2 GG2+sC3G]+sC3G2+sC3SCa 3 2 u C 十 Vo

1 2 1 3 2 3 3 4 2 4 Y Y Y Y Y Y Y Y Y YNN TT T FB FF FB FF        3 1 2 3 1 3 2 3 4 4 2 G G s C G s C G s C s C s C G T      有 ： C 3 C4 2 R1 R 4 1 2 u i u o   1 3 2 C 3 C4 R1 4 R 2 有： （P365：图10 - 3 ）

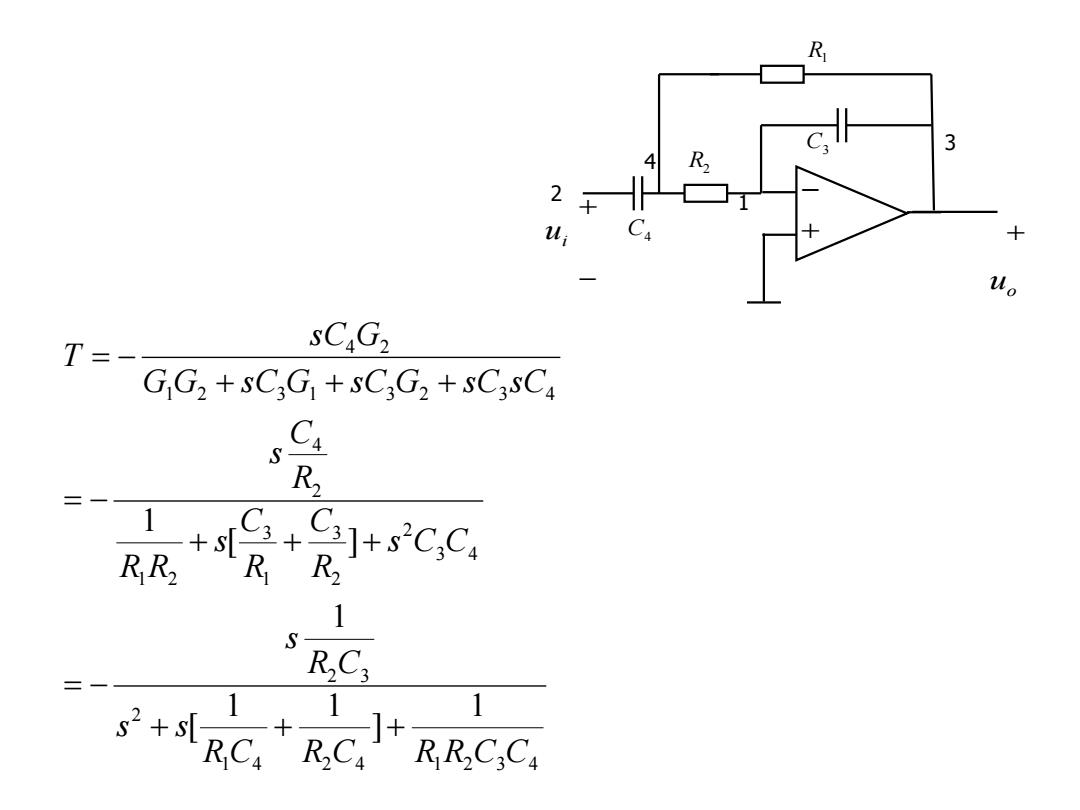
R 3 R 2 + Mo sCG2 GG2+sC3G+sC3G2+sC3sCa Ca R2 1+ C+ R sCCa 1 RC; RR.C.Ca

1 4 2 4 1 2 3 4 2 2 3 3 4 2 23 13 1 2 24 1 2 3 1 3 2 3 4 4 2 1 ] 1 1 [ 1 [ ] 1 R C R C R R C C s s R C s s C C RC RC s R R RC s G G sC G sC G sC sC sC G T                u i u o   1 3 2 C 3 C4 R1 4 R 2

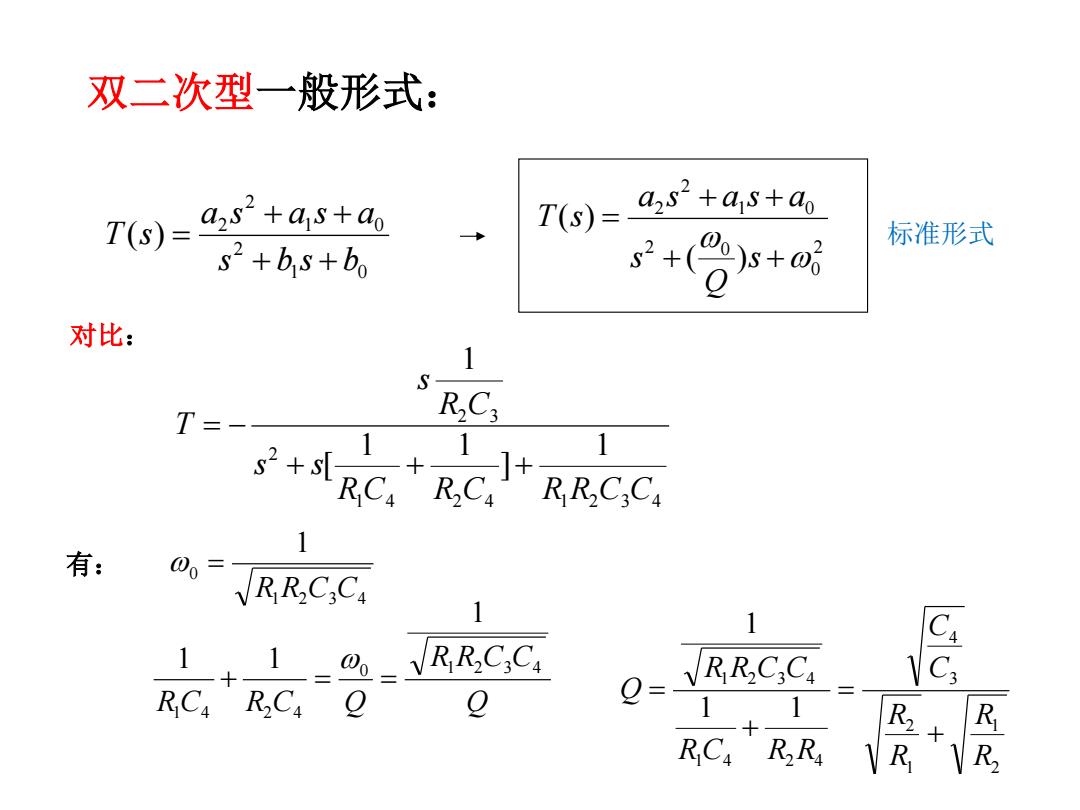
双二次型一般形式： azs"+as+ao 7(s)= azs2+as+ao T(s)= 00)s+o6 标准形式 s2+bs+b0 对比： 1 RC; T一 1 有： o-RRC;C. 1+1=@;C;C: 0= RRC3Ca RC RC 11 R+ R RCa RRa RR2

1 0 2 1 0 2 2 ( ) s b s b a s a s a T s      双二次型一般形式： 2 0 2 0 1 0 2 2 ( ) ( )        s Q s a s a s a T s 1 4 2 4 1 2 3 4 2 2 3 1 ] 1 1 [ 1 R C R C R R C C s s R C s T      对比： 1 2 3 4 0 1 R R C C 有：   Q R R C C R C R C Q 0 1 2 3 4 1 4 2 4 1 1 1     2 1 1 2 3 4 1 4 2 4 1 2 3 4 1 1 1 R R R R C C R C R R R R C C Q     标准形式

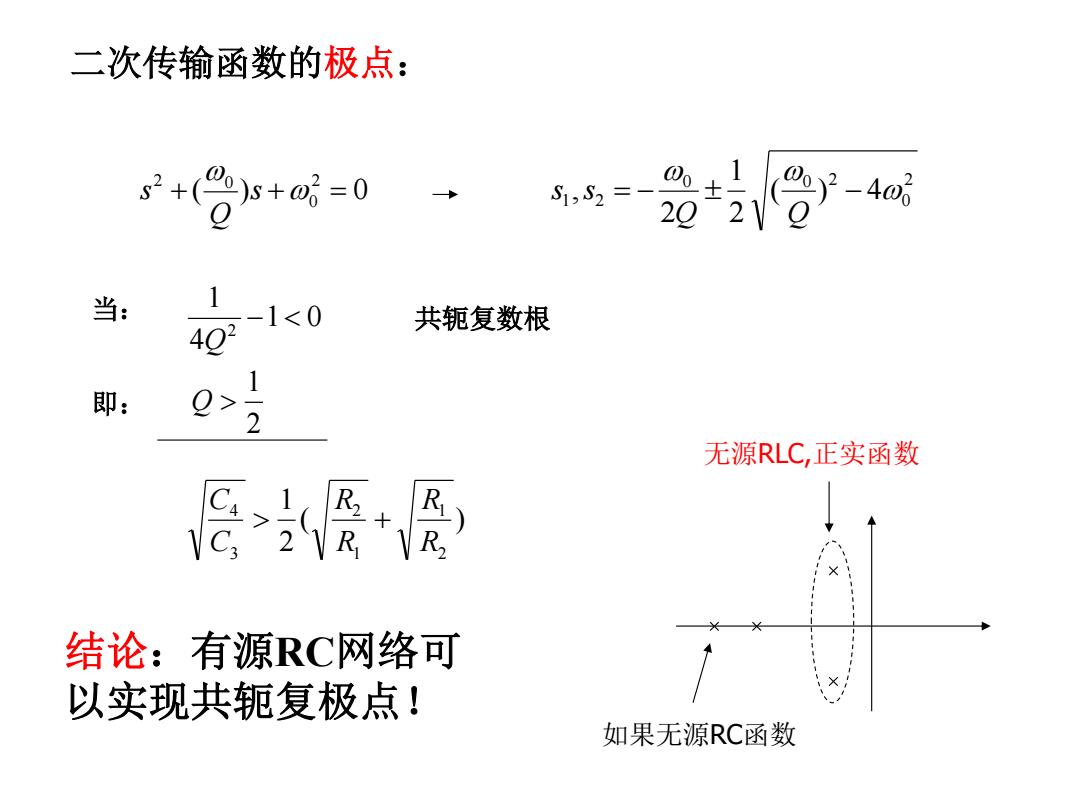
二次传输函数的极点： s2+0 s+0=0 2-4 20 当： <0 共轭复数根 即 2 无源RLC,正实函数 侣图图 结论：有源RC网络可 以实现共轭复极点！ 如果无源RC函数

2 0 0 0 2 1 2 ( ) 4 2 1 2 ,        Q Q s s 二次传输函数的极点： ( ) 0 2 0 2 0     s Q s 1 0 4 1 2   Q 当： 即： 2 1 Q  ( ) 2 1 2 1 1 2 3 4 R R R R C C   共轭复数根 如果无源RC函数 无源RLC,正实函数 结论：有源RC网络可 以实现共轭复极点！